Difference between revisions of "Quantile"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 19: | Line 19: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> L. Breiman, "Statistics" , Houghton Mifflin (1973) pp. 231ff {{MR|0359089}} {{ZBL|0289.62001}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> H. Cramér, "Mathematical methods of statistics" , Princeton Univ. Press (1946) pp. 181; 367 {{MR|0016588}} {{ZBL|0063.01014}} </TD></TR></table> |
Revision as of 10:32, 27 March 2012
One of the numerical characteristics of a probability distribution. For a real random variable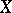 
with distribution function 
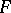, by a quantile of order 
, 
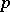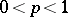, one means the number 
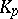for which 
, 
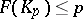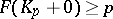. If 
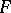is a continuous strictly-monotone function, then 
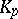is the unique solution of the equation 
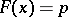, that is, 
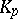is the function of 
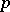inverse to the function 
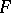. If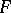 
is continuous and 
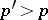, then the probability of the inequality 
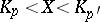, is equal to 
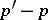. The quantile 
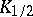is the median (in statistics) of the random variable 
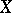. The quantiles 
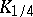and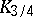 
are called the quartiles, and 
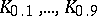, the deciles. The values of the quantiles for suitable values of 
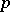enable one to form an idea about the distribution function.
For example, for the normal distribution (see Fig.)
 |
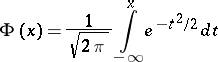the graph of the function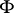 
can be drawn from the deciles: 
; 
; 
; 
; 
; 
; 
; 
; 
.
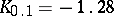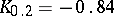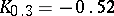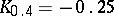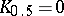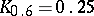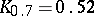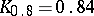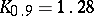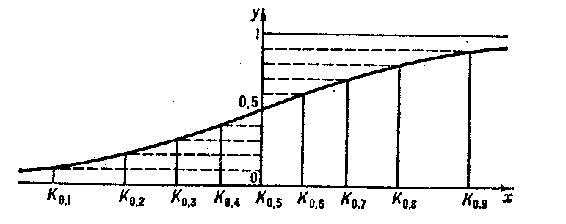
Figure: q076270a
The quartiles of the normal distribution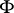 
are 
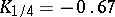and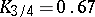 
.
Comments
References
| [a1] | L. Breiman, "Statistics" , Houghton Mifflin (1973) pp. 231ff MR0359089 Zbl 0289.62001 |
| [a2] | H. Cramér, "Mathematical methods of statistics" , Princeton Univ. Press (1946) pp. 181; 367 MR0016588 Zbl 0063.01014 |
Quantile. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Quantile&oldid=14159