Jump process

A stochastic process that changes its state only at random moments of time forming an increasing sequence. The term "jump process" is sometimes applied to any process with piecewise-constant trajectories.

An important class of jump processes is formed by Markov jump processes. A Markov process is a jump process if its transition function is such that

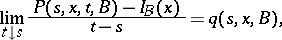(1)

where is the indicator of the set in the phase space , and if the regularity condition holds, i.e. the convergence in (1) is uniform and the kernel satisfies certain boundedness and continuity conditions.

Let

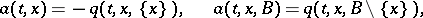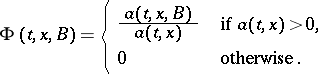These quantities admit the following interpretation: up to (as ), is the probability that in the time interval 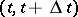the process leaves the state , and (for ) is the conditional probability that the process hits the set , provided that it leaves the state at the time .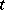

When the regularity conditions hold, the transition function of a jump process is differentiable with respect to 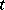when and with respect to when , and satisfies the forward and backward Kolmogorov equation with corresponding boundary conditions:

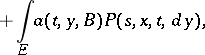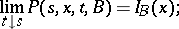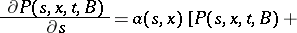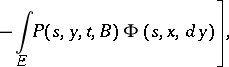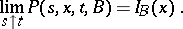Let be a strictly Markov jump process continuous from the right, let be the moment of the -th jump of the process, 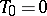, let , let 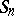be the duration of remaining in state , let be the moment of cut-off, and let , where is a point outside . Then the sequence forms a homogeneous Markov chain. Note that if is a homogeneous Markov process, then at a prescribed , is exponentially distributed with parameter .

A natural generalization of Markov jump processes are semi-Markov jump processes, for which the sequence is a Markov chain but the duration of remaining in the state depends on and 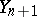, and has an arbitrary distribution.

In the investigation of general jump processes, the so-called martingale approach has proved fruitful. Within the boundaries of this approach one can obtain meaningful results without additional assumptions about the probability structure of the processes. In the martingale approach one assumes that on the probability space 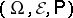of a given jump process a non-decreasing right-continuous family of 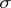-algebras 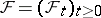, , is fixed such that the random variable is -measurable for every , so that the are Markov moments.

Let be a predictable sigma-algebra on , and put . A random measure on is said to be predictable if for any non-negative -measurable function the process , where

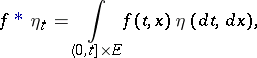is predictable.

Let be the jump measure of , that is, the integral random measure on given by

Under very general conditions on 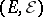(that hold, for example, when 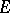is a complete separable metric space with a Borel 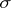-algebra ), there is a predictable random measure such that either of the following two equivalent conditions hold:

1) for any non-negative -measurable function ;

2) for all and 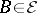the process

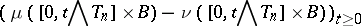is a martingale emanating from zero.

The predictable random measure is uniquely defined up to a set of -measure zero and is called the compensator (or dual predictable projection) of 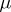. One can choose a variant of such that

(2)

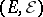Let be the space of trajectories of a jump process , taking values in , let , , and let be a probability measure for which (2) holds. Then there is a probability measure on , which is also unique, such that is the compensator of with respect to and such that the restriction of to coincides with . The proof of this relies on an explicit formula relating the conditional distributions of the variables to the compensator, which in a number of cases has turned out to be a more convenient means of describing jump processes.

A jump process is a stochastic process with independent increments if and only if the corresponding compensator is determinate.

References

[1]	A.N. [A.N. Kolmogorov] Kolmogoroff, "Ueber die analytischen Methoden in der Wahrscheinlichkeitstheorie" Math. Ann. , 104 (1931) pp. 415–458
[2]	I.I. [I.I. Gikhman] Gihman, A.V. [A.V. Skorokhod] Skorohod, "The theory of stochastic processes" , 2 , Springer (1975) pp. Chapt. 3 (Translated from Russian)
[3]	J. Jacod, "Calcul stochastique et problèmes de martingales" , Lect. notes in math. , 714 , Springer (1979)

References

[a1]	E.B. Dynkin, "Markov processes", I, Springer (1965) pp. Chapt. 3 (Translated from Russian)
[a2]	W. Feller, "An introduction to probability theory and its applications", 2, Wiley (1966) pp. Chapt. X
[a3]	M. Rosenblatt, "Random processes", Springer (1974)
[a4]	L.P. Breiman, "Probability", Addison-Wesley (1968)