Difference between revisions of "Hardy-Littlewood theorem"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (moved Hardy–Littlewood theorem to Hardy-Littlewood theorem: ascii title) |
(No difference)
| |
Revision as of 18:52, 24 March 2012
The Hardy–Littlewood theorem in the theory of functions of a complex variable: If 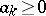 ,
, 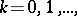 and if the power series
and if the power series
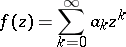 |
with radius of convergence 1 satisfies on the real axis the asymptotic equality
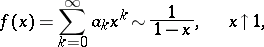 |
then the partial sums 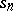 satisfy the asymptotic equality
satisfy the asymptotic equality
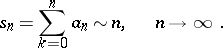 |
This theorem was established by G.H. Hardy and J.E. Littlewood [1] and is one of the Tauberian theorems.
References
| [1] | G.H. Hardy, J.E. Littlewood, "Tauberian theorems concerning power series and Dirichlet's series whose coefficients are positive" Proc. London. Math. Soc. (2) , 13 (1914) pp. 174–191 |
| [2] | E.C. Titchmarsh, "The theory of functions" , Oxford Univ. Press (1979) |
E.D. Solomentsev
The Hardy–Littlewood theorem on a non-negative summable function. A theorem on integral properties of a certain function connected with the given one. It was established by G.H. Hardy and J.E. Littlewood [1]. Let 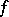 be a non-negative summable function on
be a non-negative summable function on 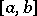 , and let
, and let
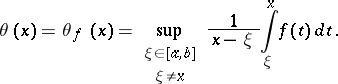 |
Then:
1) If 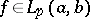 ,
, 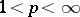 , then
, then
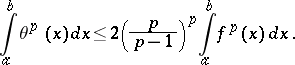 |
2) If 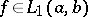 , then for all
, then for all 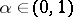 ,
,
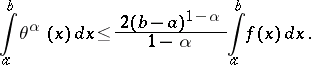 |
3) If 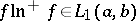 , then
, then
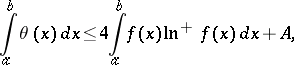 |
where 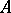 depends only on
depends only on 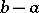 . Here
. Here
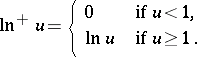 |
Let 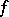 be a
be a 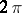 -periodic function that is summable on
-periodic function that is summable on 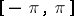 , and let
, and let
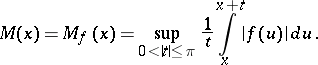 |
Then 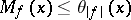 , where
, where 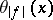 is constructed for
is constructed for 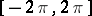 . From the theorem for
. From the theorem for 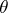 one obtains integral inequalities for
one obtains integral inequalities for 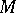 .
.
References
| [1] | G.H. Hardy, J.E. Littlewood, "A maximal theorem with function-theoretic applications" Acta. Math. , 54 (1930) pp. 81–116 |
| [2] | A. Zygmund, "Trigonometric series" , 1 , Cambridge Univ. Press (1988) |
A.A. Konyushkov
Comments
The function 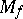 is called the Hardy–Littlewood maximal function for
is called the Hardy–Littlewood maximal function for 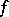 .
.
References
| [a1] | E.M. Stein, G. Weiss, "Fourier analysis on Euclidean spaces" , Princeton Univ. Press (1971) |
Hardy-Littlewood theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hardy-Littlewood_theorem&oldid=13786