Difference between revisions of "Branch index"
From Encyclopedia of Mathematics
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 6: | Line 6: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> G. Springer, "Introduction to Riemann surfaces" , Addison-Wesley (1957) pp. Chapt.10 {{MR|0092855}} {{ZBL|0078.06602}} </TD></TR></table> |
| Line 14: | Line 14: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> D. Mumford, "Algebraic geometry" , '''1. Complex projective varieties''' , Springer (1976) {{MR|0453732}} {{ZBL|0356.14002}} </TD></TR></table> |
Revision as of 21:50, 30 March 2012
The sum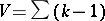 
of the orders of the branch points (cf. Branch point) of a compact Riemann surface 
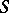, regarded as an 
-sheeted covering surface over the Riemann sphere, extended over all finite and infinitely-distant branch points of 
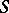. The branch index is connected with the genus 
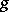and number of sheets 
of 
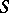by:
 |
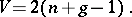See also Riemann surface.
References
| [1] | G. Springer, "Introduction to Riemann surfaces" , Addison-Wesley (1957) pp. Chapt.10 MR0092855 Zbl 0078.06602 |
Comments
References
| [a1] | D. Mumford, "Algebraic geometry" , 1. Complex projective varieties , Springer (1976) MR0453732 Zbl 0356.14002 |
How to Cite This Entry:
Branch index. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Branch_index&oldid=13651
Branch index. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Branch_index&oldid=13651
This article was adapted from an original article by E.D. Solomentsev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article