Dini-Lipschitz criterion

If a continuous 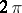-periodic function 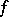satisfies the condition

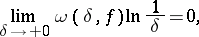where 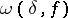is the modulus of continuity of the function 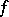, then its Fourier series converges uniformly to it on the entire real axis. The criterion was demonstrated by U. Dini [1], and also by R. Lipschitz for the special case when 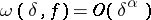, , 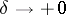for any 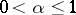[2]. The Dini–Lipschitz criterion is a final (sharp) statement in the following sense. If is an arbitrary modulus of continuity satisfying the condition

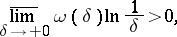then there exists a continuous 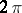-periodic function 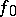whose Fourier series diverges at some point, while 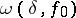satisfies the condition .

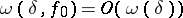References

[1]	U. Dini, "Sopra la serie di Fourier" , Pisa (1872)
[2]	R. Lipschitz, "De explicatione per series trigonometricas instituenda functionum unius variabilis arbitrariarum, etc." J. Reine Angew. Math. , 63 : 2 (1864) pp. 296–308
[3]	H. Lebesgue, "Sur la répresentation trigonométrique approchée des fonctions satisfiasants à une condition de Lipschitz" Bull. Soc. Math. France , 38 (1910) pp. 184–210
[4]	S.M. Nikol'skii, "On the Dini–Lipschitz condition for convergence of Fourier series" Doklady Akad. Nauk SSSR , 73 : 3 (1950) pp. 457–460 (In Russian)
[5]	N.K. [N.K. Bari] Bary, "A treatise on trigonometric series" , Pergamon (1964) (Translated from Russian)