Difference between revisions of "Quasi-coherent sheaf"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 13: | Line 13: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> R. Hartshorne, "Algebraic geometry" , Springer (1977) pp. 111–115; 126 {{MR|0463157}} {{ZBL|0367.14001}} </TD></TR></table> |
Revision as of 21:55, 30 March 2012
A sheaf of modules locally defined by generators and relations. More precisely, let  be a topological space and let
be a topological space and let  be a sheaf of rings on
be a sheaf of rings on  ; a sheaf
; a sheaf 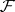 of
of  -modules is called quasi-coherent if for any point
-modules is called quasi-coherent if for any point  there is an open neighbourhood
there is an open neighbourhood  and an exact sequence of sheaves of
and an exact sequence of sheaves of  -modules
-modules
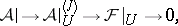 |
where 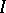 and
and 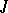 are certain sets,
are certain sets, 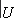 denotes the restriction of a sheaf to
denotes the restriction of a sheaf to  and
and  is the direct sum of
is the direct sum of 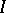 copies of
copies of 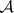 . A quasi-coherent sheaf is similarly defined on a topologized category with a sheaf of rings.
. A quasi-coherent sheaf is similarly defined on a topologized category with a sheaf of rings.
If  is an affine scheme, then the association
is an affine scheme, then the association  gives rise to an equivalence of the category of quasi-coherent sheaves of
gives rise to an equivalence of the category of quasi-coherent sheaves of 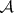 -modules and the category of
-modules and the category of 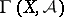 -modules. As a result of this, quasi-coherent sheaves find broad application in the theory of schemes (see also Coherent sheaf; Scheme).
-modules. As a result of this, quasi-coherent sheaves find broad application in the theory of schemes (see also Coherent sheaf; Scheme).
Comments
References
| [a1] | R. Hartshorne, "Algebraic geometry" , Springer (1977) pp. 111–115; 126 MR0463157 Zbl 0367.14001 |
Quasi-coherent sheaf. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Quasi-coherent_sheaf&oldid=13381