Kellogg-Evans theorem

Kellogg's lemma

The set of all irregular points of the boundary (cf. Irregular boundary point) of an arbitrary domain in the Euclidean space , , with respect to a generalized solution of the Dirichlet problem for in the sense of Wiener–Perron (see Perron method) has capacity zero, is a polar set and has type (cf. Set of type ()). A corollary of the Kellogg–Evans theorem is that if is a compact set of positive capacity in and 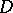is the connected component of the complement containing the point at infinity, then there exists on the boundary 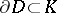at least one regular point. The Kellogg–Evans theorem was stated by O.D. Kellogg [1] as a conjecture, and was first proved by G.C. Evans [2].

References

[1]	O.D. Kellogg, "Foundations of potential theory" , F. Ungar (1929) (Re-issue: Springer, 1967)
[2]	G.C. Evans, "Application of Poincaré's sweeping-out process" Proc. Nat. Acad. Sci. USA , 19 (1933) pp. 457–461
[3]	M.V. Keldysh, "On the solvability and stability of the Dirichlet problem" Uspekhi Mat. Nauk , 8 (1941) pp. 171–231 (In Russian)
[4]	M. Brélot, "Eléments de la théorie classique du potentiel" , Sorbonne Univ. Centre Doc. Univ. , Paris (1959)