Difference between revisions of "Rational mapping"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 10: | Line 10: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> I.R. Shafarevich, "Basic algebraic geometry" , Springer (1977) (Translated from Russian) {{MR|0447223}} {{ZBL|0362.14001}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> H. Hironaka, "Resolution of singularities of an algebraic variety over a field of characteristic zero I" ''Ann. of Math.'' , '''79''' : 1–2 (1964) pp. 109–326 {{MR|0199184}} {{ZBL|0122.38603}} </TD></TR></table> |
Revision as of 21:55, 30 March 2012
A generalization of the concept of a rational function on an algebraic variety. Namely, a rational mapping from an irreducible algebraic variety 
to an algebraic variety 
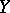(both defined over a field 
) is an equivalent class of pairs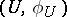 
, where 
is a non-empty open subset of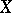 
and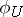 
is a morphism from 
to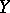 
. Two pairs 
and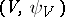 
are said to be equivalent if 
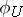and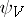 
coincide on 
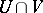. In particular, a rational mapping from a variety 
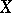to an affine line is a rational function on 
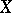. For every rational mapping 
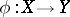there is a pair 
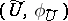such that 
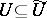for all equivalent pairs 
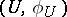and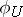 
is the restriction of 
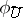to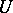 
. The open subset 
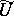is called the domain of regularity of the rational mapping 
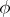, and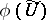 
is the image of the variety 
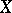(written 
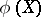) under 
.
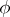If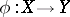 
is a rational mapping of algebraic varieties and 
is dense in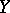 
, then 
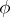determines an imbedding of fields, 
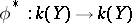. Conversely, an imbedding of the fields of rational functions 
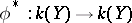determines a rational mapping from 
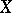to 
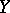. If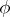 
induces an isomorphism of the fields 
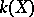and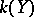 
of rational functions, then 
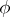is called a birational mapping.
The set of points of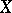 
at which the rational mapping 
is not regular has codimension 1, in general. But if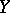 
is complete and 
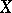is smooth and irreducible, then this set has codimension at least 2. If 
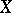and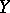 
are complete irreducible varieties over an algebraically closed field of characteristic 0, then the rational mapping 
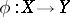can be included in a commutative diagram (see [2]):
 | (*) |
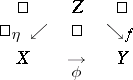where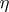 
, 
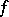are morphisms of an algebraic variety 
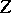and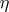 
is a composite of monoidal transformations (cf. Monoidal transformation). If 
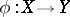is a birational mapping of complete non-singular surfaces, then there exists a diagram (*) in which both 
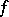and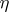 
are composites of monoidal transformations with non-singular centres (Zariski's theorem), that is, every birational mapping of complete non-singular surface decomposes into monoidal transformations with non-singular centres and their inverses. In the case when 
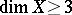, the question of whether every birational mapping can be decomposed in this way is open (1990).
References
| [1] | I.R. Shafarevich, "Basic algebraic geometry" , Springer (1977) (Translated from Russian) MR0447223 Zbl 0362.14001 |
| [2] | H. Hironaka, "Resolution of singularities of an algebraic variety over a field of characteristic zero I" Ann. of Math. , 79 : 1–2 (1964) pp. 109–326 MR0199184 Zbl 0122.38603 |
Rational mapping. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Rational_mapping&oldid=13320