Difference between revisions of "Isothermal coordinates"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 25: | Line 25: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> W. Blaschke, K. Leichtweiss, "Elementare Differentialgeometrie" , Springer (1973)</TD></TR></table> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> W. Blaschke, K. Leichtweiss, "Elementare Differentialgeometrie" , Springer (1973) {{MR|0350630}} {{ZBL|0264.53001}} </TD></TR></table> |
Revision as of 12:11, 27 September 2012
Coordinates of a two-dimensional Riemannian space in which the square of the line element has the form:
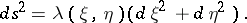 |
Isothermal coordinates specify a conformal mapping of the two-dimensional Riemannian manifold into the Euclidean plane. Isothermal coordinates can always be introduced in a compact domain of a regular two-dimensional manifold. The Gaussian curvature can be calculated in isothermal coordinates by the formula:
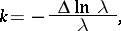 |
where  is the Laplace operator.
is the Laplace operator.
Isothermal coordinates are also considered in two-dimensional pseudo-Riemannian spaces; the square of the line element then has the form:
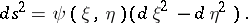 |
Here, frequent use is made of coordinates  which are naturally connected with isothermal coordinates and in which the square of the line element has the form:
which are naturally connected with isothermal coordinates and in which the square of the line element has the form:
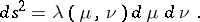 |
In this case the lines  and
and  are isotropic geodesics and the coordinate system
are isotropic geodesics and the coordinate system  is called isotropic. Isotropic coordinates are extensively used in general relativity theory.
is called isotropic. Isotropic coordinates are extensively used in general relativity theory.
Comments
References
| [a1] | W. Blaschke, K. Leichtweiss, "Elementare Differentialgeometrie" , Springer (1973) MR0350630 Zbl 0264.53001 |
Isothermal coordinates. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Isothermal_coordinates&oldid=13178