Difference between revisions of "Projective scheme"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 10: | Line 10: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> D. Mumford, "Algebraic geometry" , '''1. Complex projective varieties''' , Springer (1976) {{MR|0453732}} {{ZBL|0356.14002}} </TD></TR></table> |
| Line 18: | Line 18: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> R. Hartshorne, "Algebraic geometry" , Springer (1977) pp. 91 {{MR|0463157}} {{ZBL|0367.14001}} </TD></TR></table> |
Revision as of 21:55, 30 March 2012
A closed subscheme (cf. Scheme) of a projective space  . In homogeneous coordinates
. In homogeneous coordinates  on
on  , a projective scheme is given by a system of homogeneous algebraic equations
, a projective scheme is given by a system of homogeneous algebraic equations
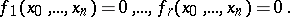 |
Every projective scheme is complete (compact in the case  ); conversely, a complete scheme is projective if there is an ample invertible sheaf (cf. Ample sheaf; Invertible sheaf) on it. There are also other criteria of projectivity.
); conversely, a complete scheme is projective if there is an ample invertible sheaf (cf. Ample sheaf; Invertible sheaf) on it. There are also other criteria of projectivity.
A generalization of the concept of a projective scheme is a projective morphism. A morphism  of schemes is called projective (and
of schemes is called projective (and  is called a scheme projective over
is called a scheme projective over  ) if
) if  is a closed subscheme of the projective fibre bundle
is a closed subscheme of the projective fibre bundle 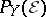 , where
, where 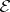 is a locally free
is a locally free 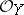 -module. A composite of projective morphisms is projective. The projectivity of a morphism is preserved also under a base change; in particular, the fibres of a projective morphism are projective schemes (but not conversely). If a scheme
-module. A composite of projective morphisms is projective. The projectivity of a morphism is preserved also under a base change; in particular, the fibres of a projective morphism are projective schemes (but not conversely). If a scheme 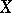 is projective and
is projective and  is a finite surjective morphism, then
is a finite surjective morphism, then 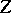 is also projective.
is also projective.
Any projective scheme (over 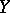 ) can be obtained using the construction of the projective spectrum (cf. Projective spectrum of a ring). Restricting to the case of an affine base,
) can be obtained using the construction of the projective spectrum (cf. Projective spectrum of a ring). Restricting to the case of an affine base, 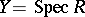 , suppose that
, suppose that 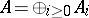 is a graded
is a graded 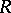 -algebra with the
-algebra with the 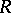 -module
-module  being of finite type and generating the algebra
being of finite type and generating the algebra 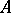 , and suppose that
, and suppose that  is the set of homogeneous prime ideals
is the set of homogeneous prime ideals 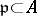 not containing
not containing 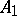 . Equipped with the natural topology and a structure sheaf, the set
. Equipped with the natural topology and a structure sheaf, the set 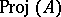 is a projective
is a projective 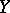 -scheme; moreover, any projective
-scheme; moreover, any projective 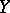 -scheme has such a form.
-scheme has such a form.
References
| [1] | D. Mumford, "Algebraic geometry" , 1. Complex projective varieties , Springer (1976) MR0453732 Zbl 0356.14002 |
Comments
Given a vector bundle 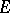 over
over 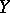 (or, equivalently, a locally free
(or, equivalently, a locally free 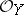 -module
-module 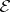 ), the associated projective bundle, or projective fibre bundle, has as fibre over
), the associated projective bundle, or projective fibre bundle, has as fibre over 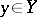 the projective space
the projective space 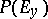 of all one-dimensional subspaces of the vector space
of all one-dimensional subspaces of the vector space 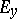 .
.
References
| [a1] | R. Hartshorne, "Algebraic geometry" , Springer (1977) pp. 91 MR0463157 Zbl 0367.14001 |
Projective scheme. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Projective_scheme&oldid=13162