Difference between revisions of "Fatou theorem (on Lebesgue integrals)"
From Encyclopedia of Mathematics
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 6: | Line 6: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> P. Fatou, "Séries trigonométriques et séries de Taylor" ''Acta Math.'' , '''30''' (1906) pp. 335–400</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> S. Saks, "Theory of the integral" , Hafner (1952) (Translated from French)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> I.P. Natanson, "Theorie der Funktionen einer reellen Veränderlichen" , H. Deutsch , Frankfurt a.M. (1961) (Translated from Russian)</TD></TR></table> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> P. Fatou, "Séries trigonométriques et séries de Taylor" ''Acta Math.'' , '''30''' (1906) pp. 335–400 {{MR|1555035}} {{ZBL|37.0283.01}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> S. Saks, "Theory of the integral" , Hafner (1952) (Translated from French) {{MR|0167578}} {{ZBL|1196.28001}} {{ZBL|0017.30004}} {{ZBL|63.0183.05}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> I.P. Natanson, "Theorie der Funktionen einer reellen Veränderlichen" , H. Deutsch , Frankfurt a.M. (1961) (Translated from Russian) {{MR|0640867}} {{MR|0409747}} {{MR|0259033}} {{MR|0063424}} {{ZBL|0097.26601}} </TD></TR></table> |
| Line 18: | Line 18: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> E. Hewitt, K.R. Stromberg, "Real and abstract analysis" , Springer (1965)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> P.R. Halmos, "Measure theory" , v. Nostrand (1950)</TD></TR></table> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> E. Hewitt, K.R. Stromberg, "Real and abstract analysis" , Springer (1965) {{MR|0188387}} {{ZBL|0137.03202}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> P.R. Halmos, "Measure theory" , v. Nostrand (1950) {{MR|0033869}} {{ZBL|0040.16802}} </TD></TR></table> |
Revision as of 11:59, 27 September 2012
A theorem on passing to the limit under a Lebesgue integral: If a sequence of measurable (real-valued) non-negative functions 
converges almost-everywhere on a set 
to a function 
, then
 |
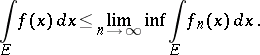It was first proved by P. Fatou [1]. In the statement of it 
is often replaced by 
.
References
| [1] | P. Fatou, "Séries trigonométriques et séries de Taylor" Acta Math. , 30 (1906) pp. 335–400 MR1555035 Zbl 37.0283.01 |
| [2] | S. Saks, "Theory of the integral" , Hafner (1952) (Translated from French) MR0167578 Zbl 1196.28001 Zbl 0017.30004 Zbl 63.0183.05 |
| [3] | I.P. Natanson, "Theorie der Funktionen einer reellen Veränderlichen" , H. Deutsch , Frankfurt a.M. (1961) (Translated from Russian) MR0640867 MR0409747 MR0259033 MR0063424 Zbl 0097.26601 |
Comments
This result is usually called Fatou's lemma. It holds in a more general form: If 
is a measure space, 
is 
-measurable for 
and 
for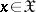 
, then
 |
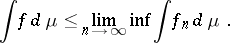It is not necessary that the sequence converges.
References
| [a1] | E. Hewitt, K.R. Stromberg, "Real and abstract analysis" , Springer (1965) MR0188387 Zbl 0137.03202 |
| [a2] | P.R. Halmos, "Measure theory" , v. Nostrand (1950) MR0033869 Zbl 0040.16802 |
How to Cite This Entry:
Fatou theorem (on Lebesgue integrals). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fatou_theorem_(on_Lebesgue_integrals)&oldid=12617
Fatou theorem (on Lebesgue integrals). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fatou_theorem_(on_Lebesgue_integrals)&oldid=12617
This article was adapted from an original article by T.P. Lukashenko (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article