Difference between revisions of "Resolution of singularities"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 22: | Line 22: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> S.S. Abhyankar, "Resolution of singularities of embedded algebraic surfaces" , Acad. Press (1966) {{MR|0217069}} {{ZBL|0147.20504}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> J. Lipman, "Introduction to resolution of singularities" R. Hartshorne (ed.) , ''Algebraic geometry (Arcata, 1974)'' , ''Proc. Symp. Pure Math.'' , '''29''' , Amer. Math. Soc. (1975) pp. 187–230 {{MR|0389901}} {{ZBL|0306.14007}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> H. Hironaka, "Resolution of singulariies of an algebraic variety over a field of characteristic zero I, II" ''Ann. of Math.'' , '''79''' (1964) pp. 109–326</TD></TR></table> |
Revision as of 21:56, 30 March 2012
desingularization
The replacement of a singular algebraic variety by a birationally isomorphic non-singular variety. More precisely, a resolution of singularities of an algebraic variety 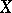 over a ground field
over a ground field  is a proper birational morphism
is a proper birational morphism 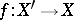 such that the variety
such that the variety  is non-singular (smooth) (cf. Proper morphism; Birational morphism). A resolution of singularities of a scheme, of a complex-analytic space, etc. is defined analogously. The existence of a resolution of singularities enables one to reduce many questions to non-singular varieties, and in studying these one can use intersection theory and the apparatus of differential forms.
is non-singular (smooth) (cf. Proper morphism; Birational morphism). A resolution of singularities of a scheme, of a complex-analytic space, etc. is defined analogously. The existence of a resolution of singularities enables one to reduce many questions to non-singular varieties, and in studying these one can use intersection theory and the apparatus of differential forms.
Usually a resolution of singularities is the result of successive application of monoidal transformations (cf. Monoidal transformation). It is known that if the centre 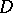 of a monoidal transformation
of a monoidal transformation 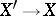 is admissible (that is,
is admissible (that is, 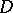 is non-singular and
is non-singular and 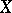 is a normal flat variety along
is a normal flat variety along 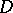 ), then the numerical characteristics of the singularity of the variety (the multiplicity, the Hilbert function, etc.) are no worse than those of
), then the numerical characteristics of the singularity of the variety (the multiplicity, the Hilbert function, etc.) are no worse than those of 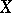 . The problem consists of choosing the centre of the blowing-up so that the singularities in
. The problem consists of choosing the centre of the blowing-up so that the singularities in 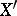 really are improved.
really are improved.
In the case of curves the problem of resolution of singularities essentially reduces to normalization. In the two-dimensional case the situation is more complicated. The existence of a resolution of singularities for any variety over a field  of characteristic zero has been proved. More precisely, for a reduced variety
of characteristic zero has been proved. More precisely, for a reduced variety 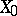 there exists a finite sequence of admissible monoidal transformations
there exists a finite sequence of admissible monoidal transformations 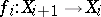 ,
, 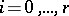 , with centres
, with centres 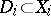 , such that
, such that 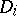 is contained in the set of singular points of
is contained in the set of singular points of 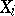 and
and 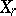 is a non-singular variety. An analogous result is true for complex-analytic spaces. In positive characteristic the existence of a resolution of singularities has been established (1983) for dimensions
is a non-singular variety. An analogous result is true for complex-analytic spaces. In positive characteristic the existence of a resolution of singularities has been established (1983) for dimensions 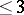 .
.
The problem of resolution of singularities is closely connected with the problem of imbedded singularities, formulated as follows. Let  be imbedded in a non-singular algebraic variety
be imbedded in a non-singular algebraic variety 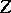 . Does there exist a proper mapping
. Does there exist a proper mapping 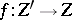 , with non-singular
, with non-singular 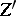 , such that a)
, such that a) 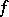 induces an isomorphism from
induces an isomorphism from 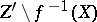 onto
onto 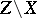 ; and b)
; and b) 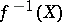 is a divisor with normal crossings? (A divisor on a non-singular variety has normal crossings if it is given locally by an equation
is a divisor with normal crossings? (A divisor on a non-singular variety has normal crossings if it is given locally by an equation 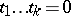 , where
, where  are part of a regular system of parameters on
are part of a regular system of parameters on 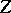 .)
.)
The problem of imbedded singularities is a particular case of the problem of trivialization of a sheaf of ideals. Let 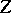 be a non-singular variety, let
be a non-singular variety, let 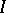 be a coherent sheaf of ideals on
be a coherent sheaf of ideals on  and let
and let 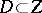 be a non-singular closed subvariety. The weak pre-image of the ideal
be a non-singular closed subvariety. The weak pre-image of the ideal 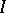 under a blowing-up
under a blowing-up  with centre in
with centre in 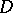 is the sheaf of ideals
is the sheaf of ideals
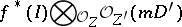 |
on 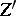 , where
, where 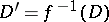 and
and 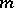 is the multiplicity of the ideal
is the multiplicity of the ideal 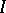 at a regular point of
at a regular point of 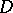 . Trivialization of a sheaf of ideals consists of finding a sequence of blowing-ups with non-singular centres for which the weak pre-image
. Trivialization of a sheaf of ideals consists of finding a sequence of blowing-ups with non-singular centres for which the weak pre-image 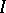 becomes the structure sheaf. Let
becomes the structure sheaf. Let 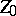 be a non-singular variety over a field of characteristic zero, let
be a non-singular variety over a field of characteristic zero, let 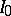 be a coherent sheaf of ideals over
be a coherent sheaf of ideals over  and, in addition, let there be given a certain divisor
and, in addition, let there be given a certain divisor 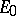 on
on 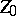 with normal crossings. Then there exists a sequence of blowing-ups
with normal crossings. Then there exists a sequence of blowing-ups 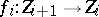 ,
, 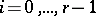 , with non-singular centres
, with non-singular centres 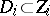 , with the following properties: If
, with the following properties: If 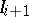 is defined as the weak pre-image of
is defined as the weak pre-image of 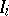 under the blowing-up
under the blowing-up 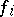 and
and 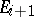 is defined to be
is defined to be  , then
, then 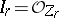 , and
, and 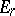 has only normal crossings (Hironaka's theorem). In addition, one may assume that
has only normal crossings (Hironaka's theorem). In addition, one may assume that 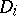 lies in the set of points of maximal multiplicity of
lies in the set of points of maximal multiplicity of 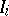 and has normal crossings with
and has normal crossings with 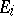 . For positive characteristic an analogous result is known only when
. For positive characteristic an analogous result is known only when 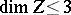 .
.
Another problem of this type is the problem of eliminating points of indeterminacy of a rational transformation. Let 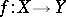 be a rational transformation of non-singular algebraic varieties. Does there exist a sequence of blowing-ups with non-singular centres
be a rational transformation of non-singular algebraic varieties. Does there exist a sequence of blowing-ups with non-singular centres
 |
such that the induced transformation 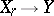 is a morphism? This problem reduces to the problem of the existence of a trivialization of a sheaf of ideals, and the answer is affirmative if
is a morphism? This problem reduces to the problem of the existence of a trivialization of a sheaf of ideals, and the answer is affirmative if 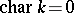 or if
or if 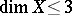 .
.
References
| [1] | S.S. Abhyankar, "Resolution of singularities of embedded algebraic surfaces" , Acad. Press (1966) MR0217069 Zbl 0147.20504 |
| [2] | J. Lipman, "Introduction to resolution of singularities" R. Hartshorne (ed.) , Algebraic geometry (Arcata, 1974) , Proc. Symp. Pure Math. , 29 , Amer. Math. Soc. (1975) pp. 187–230 MR0389901 Zbl 0306.14007 |
| [3] | H. Hironaka, "Resolution of singulariies of an algebraic variety over a field of characteristic zero I, II" Ann. of Math. , 79 (1964) pp. 109–326 |
Resolution of singularities. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Resolution_of_singularities&oldid=12523