Difference between revisions of "Rank of a Lie group"
From Encyclopedia of Mathematics
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 9: | Line 9: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> R.W. Carter, "Simple groups of Lie type" , Wiley (Interscience) (1972) pp. Chapt. 1</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> V.S. Varadarajan, "Lie groups, Lie algebras, and their representations" , Prentice-Hall (1974) {{MR|0376938}} {{ZBL|0371.22001}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> A.W. Knapp, "Representation theory of semisimple groups" , Princeton Univ. Press (1986) {{MR|0855239}} {{ZBL|0604.22001}} </TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> J.E. Humphreys, "Linear algebraic groups" , Springer (1975) pp. Sect. 35.1 {{MR|0396773}} {{ZBL|0325.20039}} </TD></TR></table> |
Revision as of 14:51, 24 March 2012
(real or complex)
The (real, respectively, complex) dimension of any Cartan subgroup of it. The rank of a Lie group coincides with the rank of its Lie algebra (see Rank of a Lie algebra). If a Lie group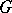 
coincides with the set of real or complex points of a linear algebraic group 
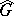, then the rank of 
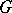coincides with the rank of 
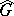(cf. Rank of an algebraic group).
Comments
References
| [a1] | R.W. Carter, "Simple groups of Lie type" , Wiley (Interscience) (1972) pp. Chapt. 1 |
| [a2] | V.S. Varadarajan, "Lie groups, Lie algebras, and their representations" , Prentice-Hall (1974) MR0376938 Zbl 0371.22001 |
| [a3] | A.W. Knapp, "Representation theory of semisimple groups" , Princeton Univ. Press (1986) MR0855239 Zbl 0604.22001 |
| [a4] | J.E. Humphreys, "Linear algebraic groups" , Springer (1975) pp. Sect. 35.1 MR0396773 Zbl 0325.20039 |
How to Cite This Entry:
Rank of a Lie group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Rank_of_a_Lie_group&oldid=12510
Rank of a Lie group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Rank_of_a_Lie_group&oldid=12510
This article was adapted from an original article by V.L. Popov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article