Difference between revisions of "Sard theorem"
From Encyclopedia of Mathematics
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 2: | Line 2: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> A. Sard, "The measure of critical values of differentiable maps" ''Bull. Amer. Math. Soc.'' , '''48''' (1942) pp. 883–890 {{MR|7523}} {{ZBL|0063.06720}} </TD></TR></table> |
====Comments==== | ====Comments==== | ||
| − | "Full measure" | + | "Full measure" is, in the Russian article, called "massive setmassive" . See also [[Singularities of differentiable mappings|Singularities of differentiable mappings]]. |
Revision as of 17:01, 15 April 2012
Let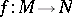 
be a 
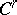-mapping of manifolds 
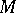and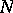 
of dimensions 
and 
, respectively; if 
, then the critical values (cf. Critical value) of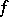 
form a set of measure zero. The set of regular values turns out to be of full measure and everywhere dense. The theorem was proved by A. Sard [1].
References
| [1] | A. Sard, "The measure of critical values of differentiable maps" Bull. Amer. Math. Soc. , 48 (1942) pp. 883–890 MR7523 Zbl 0063.06720 |
Comments
"Full measure" is, in the Russian article, called "massive setmassive" . See also Singularities of differentiable mappings.
How to Cite This Entry:
Sard theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Sard_theorem&oldid=11998
Sard theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Sard_theorem&oldid=11998
This article was adapted from an original article by M.I. Voitsekhovskii (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article