Difference between revisions of "Kullback-Leibler information"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (moved Kullback–Leibler information to Kullback-Leibler information: ascii title) |
(No difference)
| |
Revision as of 18:53, 24 March 2012
Kullback–Leibler quantity of information, Kullback–Leibler information quantity, directed divergence
For discrete distributions (cf. Discrete distribution) given by probability vectors 
, 
, the Kullback–Leibler (quantity of) information of 
with respect to 
is:
 |
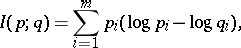where 
is the natural logarithm (cf. also Logarithm of a number).
More generally, one has:
 |
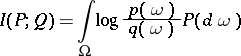for probability distributions 
and 
with densities 
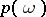and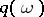 
(cf. Density of a probability distribution).
The negative of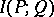 
is the conditional entropy (or relative entropy) of 
with respect to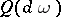 
; see Entropy.
Various notions of (asymmetric and symmetric) information distances are based on the Kullback–Leibler information.
The quantity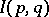 
is also called the informational divergence (see Huffman code).
See also Information distance; Kullback–Leibler-type distance measures.
References
| [a1] | S. Kullback, "Information theory and statistics" , Wiley (1959) |
| [a2] | S. Kullback, R.A. Leibler, "On information and sufficiency" Ann. Math. Stat. , 22 (1951) pp. 79–86 |
| [a3] | J. Sakamoto, M. Ishiguro, G. Kitagawa, "Akaike information criterion statistics" , Reidel (1986) |
Kullback-Leibler information. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Kullback-Leibler_information&oldid=11888