Difference between revisions of "Lie algebra, reductive"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 16: | Line 16: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> J.-P. Serre, "Lie algebras and Lie groups" , Benjamin (1965) (Translated from French) {{MR|0218496}} {{ZBL|0132.27803}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> J.-P. Serre, "Algèbres de Lie semi-simples complexes" , Benjamin (1966) {{MR|0215886}} {{ZBL|0144.02105}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> N. Bourbaki, "Elements of mathematics. Lie groups and Lie algebras" , Addison-Wesley (1975) (Translated from French) {{MR|0682756}} {{ZBL|0319.17002}} </TD></TR></table> |
Revision as of 14:50, 24 March 2012
A finite-dimensional Lie algebra over a field  of characteristic 0 whose adjoint representation is completely reducible (cf. Adjoint representation of a Lie group; Representation of a Lie algebra). The property that a Lie algebra
of characteristic 0 whose adjoint representation is completely reducible (cf. Adjoint representation of a Lie group; Representation of a Lie algebra). The property that a Lie algebra  is reductive is equivalent to any of the following properties:
is reductive is equivalent to any of the following properties:
1) the radical 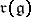 of
of  coincides with the centre
coincides with the centre 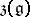 ;
;
2) 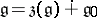 , where
, where  is a semi-simple ideal of
is a semi-simple ideal of  ;
;
3) 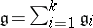 , where the
, where the 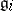 are prime ideals;
are prime ideals;
4)  admits a faithful completely-reducible finite-dimensional linear representation.
admits a faithful completely-reducible finite-dimensional linear representation.
The property that a Lie algebra is reductive is preserved by both extension and restriction of the ground field  .
.
An important class of reductive Lie algebras over  are the compact Lie algebras (see Lie group, compact). A Lie group with a reductive Lie algebra is often called a reductive Lie group. A Lie algebra over
are the compact Lie algebras (see Lie group, compact). A Lie group with a reductive Lie algebra is often called a reductive Lie group. A Lie algebra over  is reductive if and only if it is isomorphic to the Lie algebra of a reductive algebraic group over
is reductive if and only if it is isomorphic to the Lie algebra of a reductive algebraic group over  .
.
A generalization of the concept of a reductive Lie algebra is the following. A subalgebra 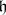 of a finite-dimensional Lie algebra
of a finite-dimensional Lie algebra  over
over  is said to be reductive in
is said to be reductive in  if the adjoint representation
if the adjoint representation 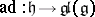 is completely reducible. In this case
is completely reducible. In this case  is a reductive Lie algebra. If
is a reductive Lie algebra. If 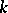 is algebraically closed, then for a subalgebra
is algebraically closed, then for a subalgebra  of
of  to be reductive it is necessary and sufficient that
to be reductive it is necessary and sufficient that 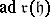 consists of semi-simple linear transformations.
consists of semi-simple linear transformations.
References
| [1] | J.-P. Serre, "Lie algebras and Lie groups" , Benjamin (1965) (Translated from French) MR0218496 Zbl 0132.27803 |
| [2] | J.-P. Serre, "Algèbres de Lie semi-simples complexes" , Benjamin (1966) MR0215886 Zbl 0144.02105 |
| [3] | N. Bourbaki, "Elements of mathematics. Lie groups and Lie algebras" , Addison-Wesley (1975) (Translated from French) MR0682756 Zbl 0319.17002 |
Lie algebra, reductive. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lie_algebra,_reductive&oldid=11403