Namespaces
Variants
Actions

Difference between revisions of "User:Boris Tsirelson/sandbox2"

From Encyclopedia of Mathematics
Jump to: navigation, search
(Undo revision 35590 by Boris Tsirelson (talk))
 
(68 intermediate revisions by the same user not shown)
Line 1: Line 1:
−
[http://math.stackexchange.com/questions/51453/is-non-standard-analysis-worth-learning MathStackExchange]
+
==Experiments==
  
−
So, in summary, I think some parts of "modern analysis" (done lightly) more effectively fulfill one's intuition about "infinitesimals" than does non-standard analysis.'
+
Note a fine distinction from [http://ada00.math.uni-bielefeld.de/MW1236/index.php/User:Boris_Tsirelson/sandbox#Experiments Ada]:
  
−
A propos whether it makes calculus any easier: that is for you to decide. From my point of view, because of the need to rigorously introduce the hyperreals and the notion of the standard part of an expression, for an absolute beginner it is just passing the buck. You either learn how to write ϵ−δ arguments, or you accept a less-intuitive number system and learn all the rules about what you can and cannot do in this system. I think that a real appreciation of non-standard analysis can only come after one has developed some fundamentals of standard analysis. In fact, for me, one of the most striking thing about non-standard analysis is that it provides an a posteriori justification why the (by modern standards) sloppy notations of Newton, Leibniz, Cauchy, etc did not result in a theory that collapses under more careful scrutiny. But that's just my opinion.
+
<center><asy>
 +
fill( box((-1,-1),(1,1)), white );
 +
draw( (-1.2,-0.5)--(1.2,-0.5) );
 +
label("Just a text",(0,0));
 +
filldraw( box((-0.7,-1),(0.7,1)), white, opacity(0) );
 +
shipout(scale(15)*currentpicture);
 +
</asy></center>
  
 +
I guess, the reason is that there Asy generates pdf file (converted into png afterwards), and here something else (probably ps).
  
−
[http://terrytao.wordpress.com/2009/12/13/approximate-bases-sunflowers-and-nonstandard-analysis/ Tao]
+
No, it seems, it generates eps, both here and there. Then, what could be the reason?
−
Reproduced in book: Epsilon of Room, Two, Volume 2 (sect. 2.11.4, pp. 227-229).
 
  
−
4. Summary
+
More.
  
−
Let me summarise with a brief list of pros and cons of switching to a nonstandard framework. First, the pros:
+
<center><asy>
 +
label("Just a text",(0,0));
 +
fill( box((-2,-1),(2,1)), white );
 +
//draw( box((-2,-1),(2,1)), green );
 +
shipout(scale(15)*currentpicture);
 +
</asy></center>
  
−
Many “first-order” parameters such as {\epsilon} or {N} disappear from view, as do various “negligible” errors. More importantly, “second-order” parameters, such as the function {F} appearing in Theorem 2, also disappear from view. (In principle, third-order and higher parameters would also disappear, though I do not yet know of an actual finitary argument in my fields of study which would have used such parameters (with the exception of Ramsey theory, where such parameters must come into play in order to generate such enormous quantities as Graham’s number).) As such, a lot of tedious “epsilon management” disappears.
 
  
−
Iterative (and often parameter-heavy) arguments can often be replaced by minimisation (or more generally, extremisation) arguments, taking advantage of such properties as the well-ordering principle, the least upper bound axiom, or compactness.
+
<center><asy>
 +
label("Just a text",(0,0));
 +
fill( box((-2,-1),(2,1)), white );
 +
draw( box((-2,-1),(2,1)), green );
 +
shipout(scale(15)*currentpicture);
 +
</asy></center>
  
−
The transfer principle lets one use “for free” any (first-order) statement about standard mathematics in the non-standard setting (provided that all objects involved are internal; see below).
+
Mysterious.
  
−
Mature and powerful theories from infinitary mathematics (e.g. linear algebra, real analysis, representation theory, topology, functional analysis, measure theory, Lie theory, ergodic theory, model theory, etc.) can be used rigorously in a nonstandard setting (as long as one is aware of the usual infinitary pitfalls, of course; see below).
+
==Three dimensions==
  
−
One can formally define terms that correspond to what would otherwise only be heuristic (or heavily parameterised and quantified) concepts such as “small”, “large”, “low rank”, “independent”, “uniformly distributed”, etc.
+
<center><asy>
 +
settings.render = 0;
  
−
The conversion from a standard result to its nonstandard counterpart, or vice versa, is fairly quick (but see below), and generally only needs to be done only once or twice per paper.
+
unitsize(100);
  
−
Next, the cons:
+
import three;
 +
import tube;
  
−
Often requires the axiom of choice, as well as a certain amount of set theory. (There are however weakened versions of nonstandard analysis that can avoid choice that are still suitable for many applications.)
+
import graph;
 +
path unitCircle = Circle((0,0),1,35);
  
−
One needs the machinery of ultralimits and ultraproducts to set up the conversion from standard to nonstandard structures.
+
currentprojection = perspective((900,-350,-650));
 +
currentlight=light(gray(0.4),specularfactor=3,viewport=false,(-0.5,-0.5,-0.75),(0,-0.5,0.5),(0.5,0.5,0.75));
 +
// currentlight=light(gray(0.4),specularfactor=3,viewport=false,(-0.5,-0.5,-0.75),(0.5,-0.5,0.5),(0.5,0.5,0.75));
  
−
The conversion usually proceeds by a proof by contradiction, which (in conjunction with the use of ultralimits) may not be particularly intuitive.
+
triple horn_start=(0,-1,0.6);
 +
triple horn_end=(0,0.4,0.2);
 +
real horn_radius=0.2;
  
−
One cannot efficiently discern what quantitative bounds emerge from a nonstandard argument (other than by painstakingly converting it back to a standard one, or by applying the tools of proof mining). (On the other hand, in particularly convoluted standard arguments, the quantitative bounds are already so poor – e.g. of iterated tower-exponential type – that losing these bounds is no great loss.)
+
real ratio=horn_end.z/(-horn_start.y);    // fractal levels ratio
  
−
One has to take some care to distinguish between standard and nonstandard objects (and also between internal and external sets and functions, which are concepts somewhat analogous to measurable and non-measurable sets and functions in measurable theory). More generally, all the usual pitfalls of infinitary analysis (e.g. interchanging limits, the need to ensure measurability or continuity) emerge in this setting, in contrast to the finitary setting where they are usually completely trivial.
+
transform3 implode_right = shift(horn_end) * scale3(ratio) * rotate(-90,X) * shift(-horn_start.y*Y);
 +
transform3 left_right = reflect(O,X,Z)*rotate(90,Y);
  
−
It can be difficult at first to conceptually visualise what nonstandard objects look like (although this becomes easier once one maps nonstandard analysis concepts to heuristic concepts such as “small” and “large” as mentioned earlier, thus for instance one can think of an unbounded nonstandard natural number as being like an incredibly large standard natural number).
+
path[] cover_with_holes = scale(horn_radius/ratio)*unitCircle^^
 +
  shift((horn_start.z,0))*scale(0.9horn_radius)*reverse(unitCircle)^^
 +
  shift((-horn_start.z,0))*scale(0.9horn_radius)*reverse(unitCircle);
 +
surface cover = surface(cover_with_holes,ZXplane);
 +
surface cover_left = shift((horn_start.x,horn_start.y,0))*cover;
 +
surface two_covers = surface(cover_left,left_right*cover_left);
  
−
It is inefficient for both nonstandard and standard arguments to coexist within a paper; this makes things a little awkward if one for instance has to cite a result from a standard mathematics paper in a nonstandard mathematics one.
+
path3 horn_axis = horn_start..horn_start+(0,0.01,0)..(0,0,0.7)..(0,0.2,0.6)..horn_end+(0,0,0.01)..horn_end;
  
−
There are philosophical objections to using mathematical structures that only exist abstractly, rather than corresponding to the “real world”. (Note though that similar objections were also raised in the past with regard to the use of, say, complex numbers, non-Euclidean geometries, or even negative numbers.)
+
surface horn = tube( horn_axis, scale(horn_radius)*unitCircle );
 +
surface two_horns = surface(horn,reflect(O,X,Y)*horn);
 +
surface two_horns = surface(horn,reflect(O,X,Y)*horn);
 +
surface four_horns = surface(two_horns,left_right*two_horns,two_covers);
  
−
Formally, there is no increase in logical power gained by using nonstandard analysis (at least if one accepts the axiom of choice); anything which can be proven by nonstandard methods can also be proven by standard ones. In practice, though, the length and clarity of the nonstandard proof may be substantially better than the standard one.
+
surface four_small_horns = implode_right*four_horns;
 +
surface eight_small_horns = surface(four_small_horns,left_right*four_small_horns);
  
−
In view of the pros and cons, I would not say that nonstandard analysis is suitable in all situations, nor is it unsuitable in all situations, but one needs to carefully evaluate the costs and benefits in a given setting; also, in some cases having both a finitary and infinitary proof side by side for the same result may be more valuable than just having one of the two proofs. My rule of thumb is that if a finitary argument is already spitting out iterated tower-exponential type bounds or worse in an argument, this is a sign that the argument “wants” to be infinitary, and it may be simpler to move over to an infinitary setting (such as the nonstandard setting).
+
surface big_surface = surface(four_horns,eight_small_horns);
 +
 
 +
real R = horn_radius/ratio;
 +
 
 +
draw ( circle((0,1,0), 1.005R, Y ), currentpen+2 );
 +
draw ( circle((horn_start.z,1.01,horn_start.x), horn_radius, Y ), currentpen+2 );
 +
draw ( circle((-horn_start.z,1.01,horn_start.x), horn_radius, Y ), currentpen+2 );
 +
 
 +
draw (big_surface, yellow);
 +
 
 +
pen blackpen = currentpen+1.5;
 +
 
 +
draw ( circle((0,-1,0), 1.005R, Y ), blackpen );
 +
draw ( circle(horn_start, 0.98horn_radius, Y ), blackpen );
 +
draw ( circle((horn_start.x,horn_start.y,-horn_start.z), 0.98horn_radius, Y ), blackpen );
 +
 
 +
real phi=0.9;  // adjust to the projection
 +
triple u = (cos(phi),0,sin(phi));
 +
draw( R*u-Y -- R*u+Y, blackpen );
 +
draw( -R*u-Y -- -R*u+Y, blackpen );
 +
 
 +
</asy></center>
 +
 
 +
 
 +
<center><asy>
 +
settings.render = 0;
 +
 
 +
size(200);
 +
import graph3;
 +
 
 +
currentprojection=perspective((2,2,5));
 +
 
 +
real R=1;
 +
real a=1;
 +
 
 +
real co=0.6;
 +
real colo=0.3;
 +
 
 +
triple f(pair t) {
 +
  return ((R+a*cos(t.y))*cos(t.x),(R+a*cos(t.y))*sin(t.x),a*sin(t.y));
 +
}
 +
 
 +
surface s=surface(f,(0,0),(2pi,2pi),20,20,Spline);
 +
 
 +
draw(s,rgb(co,co,co),meshpen=rgb(colo,colo,colo));
 +
 
 +
</asy></center>
 +
 
 +
==Sinusoid==
 +
 
 +
<center><asy>
 +
import graph;
 +
size(450);
 +
real f(real x) {return sin(x);};
 +
 
 +
real f1(real x) {return cos(x);};
 +
draw(graph(f1,-2*pi,2*pi),blue+1,"$\cos(x)$");
 +
draw(graph(f,-2*pi,2*pi),red+1,"$\sin(x)$");
 +
xaxis("$x$",Arrow);
 +
yaxis();
 +
 
 +
xtick("$\frac{\pi}{6}$",pi/6,N);
 +
xtick("$\frac{\pi}{4}$",pi/4,N);
 +
xtick("$\frac{\pi}{3}$",pi/3,N);
 +
xtick("$\frac{\pi}{2}$",pi/2,N);
 +
xtick("$\frac{3\pi}{2}$",3*pi/2,N);
 +
xtick("$\pi$",pi,N);
 +
xtick("$2\pi$",2*pi,N);
 +
xtick("$-\frac{\pi}{2}$",-pi/2,N);
 +
xtick("$-\frac{3\pi}{2}$",-3*pi/2,N);
 +
xtick("$-\pi$",-pi,N);
 +
xtick("$-2\pi$",-2*pi,N);
 +
 
 +
ytick("$1/2$",0.5,1,fontsize(8pt));
 +
ytick("$\sqrt{2}/2$",sqrt(2)/2,1,fontsize(8pt));
 +
ytick("$\sqrt{3}/2$",sqrt(3)/2,1,fontsize(8pt));
 +
ytick("$1$",1,1,fontsize(8pt));
 +
ytick("$-1/2$",-0.5,-1,fontsize(8pt));
 +
ytick("$-\sqrt{2}/2$",-sqrt(2)/2,-1,fontsize(8pt));
 +
ytick("$-\sqrt{3}/2$",-sqrt(3)/2,-1,fontsize(8pt));
 +
ytick("$-1$",-1,-1,fontsize(8pt));
 +
 
 +
attach(legend(),truepoint(E),10E,UnFill);
 +
</asy></center>
 +
 
 +
==Sinusoidal spiral==
 +
 
 +
<center><asy>
 +
import graph;
 +
size (200);
 +
 
 +
real r = 2.3;
 +
real m = 4;
 +
 
 +
real eps=10.^(-10);
 +
for  (int k=0; k<m; ++k) {
 +
  draw ( polargraph(  new real(real x) {return cos(m*x)^(1/m);}, -(pi/2m)+eps+k*2pi/m, (pi/2m)-eps+k*2pi/m ),
 +
defaultpen+1.5 );
 +
  draw ( -r*expi(-pi/2m+k*2pi/m)..r*expi(-pi/2m+k*2pi/m), dashed );
 +
  draw ( -r*expi(pi/2m+k*2pi/m)..r*expi(pi/2m+k*2pi/m), dashed );
 +
}
 +
label( "$m=4$", (0.58,0.02), fontsize(7pt) );
 +
 
 +
real eps=10.^(-2);
 +
for  (int k=0; k<m; ++k) {
 +
  draw ( polargraph(  new real(real x) {return cos(m*x)^(-1/m);}, -(pi/2m)+eps+k*2pi/m, (pi/2m)-eps+k*2pi/m ),
 +
defaultpen+1.5 );
 +
}
 +
label( "$m=-4$", (1.55,0.02), fontsize(7pt) );
 +
 
 +
label( "sinusoidal spiral: $a=1$", (0,2.3) );
 +
draw ( unitcircle, dashed );
 +
</asy></center>
 +
 
 +
==Power function==
 +
 
 +
<center><asy>
 +
import graph;
 +
picture whole;
 +
 
 +
real sc=0.8;
 +
 
 +
draw ( graph( new real(real x) {return x;}, -2, 2), red+1.2, "$y=x$" );
 +
draw ( graph( new real(real x) {return 2x;}, -1, 1), blue+1.2, "$y=2x$" );
 +
draw ( graph( new real(real x) {return x/2;}, -2, 2), green+1.2, "$y=x/2$" );
 +
 
 +
xaxis(-2.1,2.1, LeftTicks(Label(fontsize(8pt)),Step=1,step=0.2,Size=2,size=1,NoZero));
 +
yaxis(-2,2, RightTicks(Label(fontsize(8pt)),Step=0.5,step=0.1,Size=2,size=1,NoZero));
 +
labelx("$x$",(2.3,0.25));
 +
labely("$y$",(0.15,2.3));
 +
 
 +
add(scale(0.72sc,1.2sc)*legend(),(0.5,-0.75));
 +
 
 +
real mrg=1.3;
 +
draw( scale(mrg)*box((-2,-2),(2,2)), white );
 +
 
 +
add (whole,shift(-sc*230,0)*currentpicture.fit(sc*mrg*6.5cm));
 +
erase();
 +
 
 +
 
 +
draw ( graph( new real(real x) {return 1/x;}, -4, -0.25), red+1.2, "$y=1/x$" );
 +
draw ( graph( new real(real x) {return 1/x;}, 0.25, 4), red+1.2 );
 +
draw ( graph( new real(real x) {return 2/x;}, -4, -0.5), blue+1.2, "$y=2/x$" );
 +
draw ( graph( new real(real x) {return 2/x;}, 0.5, 4), blue+1.2 );
 +
draw ( graph( new real(real x) {return 1/(2x);}, -4, -0.125), green+1.2, "$y=1/(2x)$" );
 +
draw ( graph( new real(real x) {return 1/(2x);}, 0.125, 4), green+1.2 );
 +
 
 +
xaxis(-4.2,4.2, LeftTicks(Label(fontsize(8pt)),Step=2,step=0.5,Size=2,size=1,NoZero));
 +
yaxis(-4,4, RightTicks(Label(fontsize(8pt)),Step=1,step=0.2,Size=2,size=1,NoZero));
 +
labelx("$x$",(4.6,0.5));
 +
labely("$y$",(0.3,4.6));
 +
 
 +
add(scale(0.75sc,0.75sc)*legend(),(0.95,-1.2));
 +
 
 +
real mrg=1.3;
 +
draw( scale(mrg)*box((-4,-4),(4,4)), white );
 +
 
 +
add (whole,shift(0,0)*currentpicture.fit(sc*mrg*6.5cm,mrg*6.5cm,false));
 +
erase();
 +
 
 +
 
 +
draw ( graph( new real(real x) {return x^3;}, -4^(1/3), 4^(1/3)), red+1.2, "$y=x^3$" );
 +
draw ( graph( new real(real x) {return x^2;}, -2, 2), blue+1.2, "$y=x^2$" );
 +
draw ( graph( new real(real x) {return sqrt(x);}, 0, 4), green+1.2, "$y=x^{1/2}$" );
 +
draw ( graph( new real(real x) {return -sqrt(x);}, 0, 4), green+1.2 );
 +
 
 +
xaxis(-4.2,4.2, LeftTicks(Label(fontsize(8pt)),Step=2,step=0.5,Size=2,size=1,NoZero));
 +
yaxis(-4,4, RightTicks(Label(fontsize(8pt)),Step=1,step=0.2,Size=2,size=1,NoZero));
 +
labelx("$x$",(4.6,0.5));
 +
labely("$y$",(0.3,4.6));
 +
 
 +
add(scale(0.5sc,0.75sc)*legend(),(0.6,-2.5));
 +
 
 +
real mrg=1.3;
 +
draw( scale(mrg)*box((-4,-4),(4,4)), white );
 +
 
 +
add (whole,shift(sc*230,0)*currentpicture.fit(sc*mrg*6.5cm,mrg*6.5cm,false));
 +
erase();
 +
 
 +
shipout(whole);
 +
</asy></center>
 +
 
 +
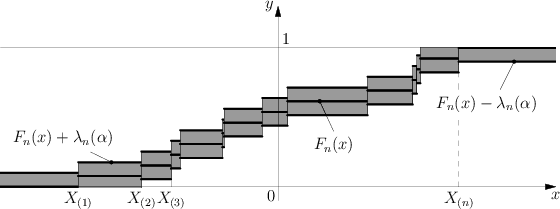
==Kolmogorov test==
 +
 
 +
<center><asy>
 +
 
 +
srand(2014011);
 +
 
 +
import stats;
 +
 
 +
int size = 13;
 +
real [] sample = new real[size+1];
 +
real lambda = 1.3/size;
 +
real width = 2.0;
 +
 
 +
for (int k=0; k<size; ++k) {
 +
  sample[k] = Gaussrand();
 +
}
 +
sample[size] = 10;
 +
 
 +
sample = sort(sample);
 +
 
 +
// for (real x : sample ) {
 +
//  write(x);
 +
// }
 +
 
 +
real x0 = -10;
 +
int k = 0;
 +
for (real x : sample ) {
 +
  filldraw( box( (x0,k/size-lambda), (x,k/size+lambda) ), rgb(0.8,0.8,0.8) );
 +
  draw( (x0,k/size-lambda)..(x,k/size-lambda), currentpen+1.5 );
 +
  draw( (x0,k/size)..(x,k/size), currentpen+1.5 );
 +
  draw( (x0,k/size+lambda)..(x,k/size+lambda), currentpen+1.5 );
 +
  k += 1;
 +
  x0 = x;
 +
  draw( (x,(k-1)/size-lambda)..(x,k/size+lambda) );
 +
}
 +
 
 +
clip( box((-width,-0.005),(width,1.005)) );
 +
 
 +
draw ((-width,0)--(width,0),Arrow);
 +
draw ((0,-0.1)--(0,1.3),Arrow);
 +
draw ((-width,1)--(width,1));
 +
 
 +
draw ((sample[2],0)..(sample[2],2/size));
 +
draw ((sample[size-1],0)..(sample[size-1],0.48), dashed);
 +
draw ((sample[size-1],0.7)..(sample[size-1],1-1/size), dashed);
 +
 
 +
label("$x$",(width,0),S);
 +
label("$y$",(0,1.3),W);
 +
label("$0$",(0,0),SW);
 +
label("$1$",(0,1),NE);
 +
 
 +
label("$X_{(1)}$",(sample[0],0),S);
 +
label("$X_{(2)}$",(sample[1],0),S);
 +
label("$X_{(3)}$",(sample[2],0),S);
 +
label("$X_{(n)}$",(sample[size-1],0),S);
 +
 
 +
label("$F_n(x)+\lambda_n(\alpha)$",(-1.55,0.35));
 +
draw ((-1.35,0.25)..(-1.2,1/size+lambda));
 +
dot((-1.2,1/size+lambda));
 +
 
 +
label("$F_n(x)$",(0.4,0.3));
 +
draw ((0.4,0.4)..(0.3,8/size));
 +
dot((0.3,8/size));
 +
 
 +
label("$F_n(x)-\lambda_n(\alpha)$",(1.5,0.6));
 +
draw ((1.6,0.7)..(1.7,1-lambda));
 +
dot((1.7,1-lambda));
 +
 
 +
shipout(scale(100,100)*currentpicture);
 +
</asy></center>
 +
 
 +
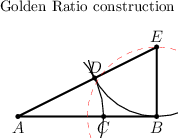
==Golden ratio==
 +
 
 +
Strangely, the figure in EoM is erroneous! ED=EB, not BD=EB.
 +
 
 +
<center><asy>
 +
 
 +
pair A=(-1,0);
 +
pair B=(0,0);
 +
pair E=(0,0.5);
 +
pair C=A+(0.5*(sqrt(5)-1),0);
 +
pair D=(-1/sqrt(5), 0.5*(1-1/sqrt(5)));
 +
 
 +
draw( A--B--E--cycle,currentpen+1.5 );
 +
dot(A,currentpen+3.5); dot(B,currentpen+3.5); dot(E,currentpen+3.5); dot(C,currentpen+3.5); dot(D,currentpen+3.5);
 +
 
 +
draw( shift(E)*scale(0.5)*unitcircle,currentpen+1 );
 +
draw( shift(A)*scale(0.5*(sqrt(5)-1))*unitcircle,currentpen+1 );
 +
 
 +
draw( shift(B)*scale(0.5)*unitcircle, dashed+red );
 +
 
 +
clip(A+(-0.15,-0.15)--B+(0.15,-0.15)--E+(0.15,0.15)--A+(-0.15,0.15)--cycle);
 +
 
 +
label("$A$",A,S); label("$B$",B,S); label("$C$",C,S);
 +
label("$E$",E,N); label("$D$",D,N);
 +
 
 +
label( "\small Golden Ratio construction", (-0.5,0.8) );
 +
 
 +
shipout(scale(100)*currentpicture);
 +
</asy></center>
 +
 
 +
 
 +
 
 +
 
 +
 
 +
 
 +
 
 +
 
 +
[Calculus: ] the art of numbering and measuring exactly a thing whose existence cannot be conceived. (Voltaire, [http://www.fordham.edu/halsall/mod/1778voltaire-newton.asp Letter XVII: On Infinites In Geometry, And Sir Isaac Newton's Chronology])
 +
 
 +
And what are these fluxions? The velocities of evanescent increments? They are neither finite quantities, nor quantities infinitely small, nor yet nothing. May we not call them ghosts of departed quantities?  (Berkeley, [http://www-history.mcs.st-and.ac.uk/Quotations/Berkeley.html The Analyst])
 +
 
 +
 
 +
WARNING: Asirra, the cat and dog CAPTCHA, is closing permanently on October 6, 2014. Please contact this site's administrator and ask them to switch to a different CAPTCHA. Thank you!

Latest revision as of 20:14, 12 December 2014

Experiments

Note a fine distinction from Ada:

I guess, the reason is that there Asy generates pdf file (converted into png afterwards), and here something else (probably ps).

No, it seems, it generates eps, both here and there. Then, what could be the reason?

More.


Mysterious.

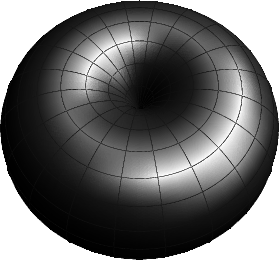
Three dimensions


Sinusoid

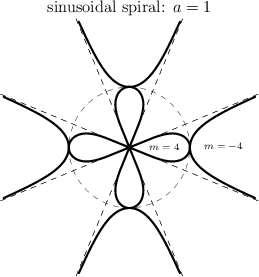
Sinusoidal spiral

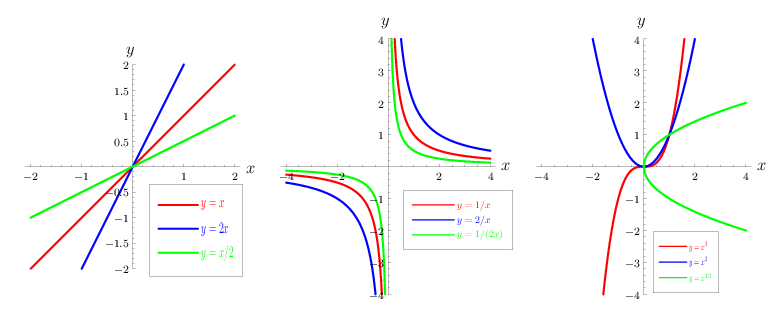
Power function

Kolmogorov test

Golden ratio

Strangely, the figure in EoM is erroneous! ED=EB, not BD=EB.





[Calculus: ] the art of numbering and measuring exactly a thing whose existence cannot be conceived. (Voltaire, Letter XVII: On Infinites In Geometry, And Sir Isaac Newton's Chronology)

And what are these fluxions? The velocities of evanescent increments? They are neither finite quantities, nor quantities infinitely small, nor yet nothing. May we not call them ghosts of departed quantities? (Berkeley, The Analyst)


WARNING: Asirra, the cat and dog CAPTCHA, is closing permanently on October 6, 2014. Please contact this site's administrator and ask them to switch to a different CAPTCHA. Thank you!

How to Cite This Entry:
Boris Tsirelson/sandbox2. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Boris_Tsirelson/sandbox2&oldid=33409
Retrieved from "https://encyclopediaofmath.org/index.php?title=User:Boris_Tsirelson/sandbox2&oldid=35591"