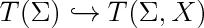|
|
| (26 intermediate revisions by the same user not shown) |
| Line 1: |
Line 1: |
| − | =Genetic Algorithms=
| + | <ref> [http://hea-www.harvard.edu/AstroStat http://hea-www.harvard.edu/AstroStat]; <nowiki> http://www.incagroup.org </nowiki>; <nowiki> http://astrostatistics.psu.edu </nowiki> </ref> |
| | | | |
| − | ==Genetic algorithms (GAs): basic form== | + | ====Notes==== |
| | + | <references /> |
| | | | |
| − | A generic GA (also known as an evolutionary algorithm [EA]) assumes a discrete search space $H$ and a function
| + | ------------------------------------------- |
| − | \[f:H\to\R,\]
| |
| − | where $H$ is a subset of the Euclidean space $\R$.
| |
| | | | |
| − | The general problem is to find
| |
| − | \[\arg\underset{X\in H}{\mathop{\min }}\,f\]
| |
| − | where $X$ is a vector of the decision variables and $f$ is the objective function.
| |
| | | | |
| − | With GAs it is customary to distinguish genotype–the encoded representation of the variables–from phenotype–the set of variables themselves. The vector $X$ is represented by a string (or chromosome) $s$ of length $l$ made up of symbols drawn from an alphabet $A$ using the mapping
| + | {| |
| − | \[c:A^l\to H\]
| + | | A || B || C |
| − | The mapping $c$ is not necessarily surjective. The range of $c$ determine the subset of $A^l$ available for exploration by a GA. The range of $c$, $\Xi$
| + | |- |
| − | \[\Xi\subseteq {{A}^{l}}\]
| + | | X || Y || Z |
| − | is needed to account for the fact that some strings in the image $A^l$ under $c$ may represent invalid solutions to the original problem.
| + | |} |
| | | | |
| − | The string length $l$ depends on the dimensions of both $H$ and $A^l$, with the elements of the string corresponding to genes and the values to alleles. This statement of genes and alleles is often referred to as genotype-phenotype mapping.
| |
| | | | |
| − | Given the statements above, the optimization becomes:
| |
| − | \[\arg\underset{S\in L}{\mathop{\min g}}\,\],
| |
| − | given the function
| |
| − | \[g(s)=f(c(s))\].
| |
| − | Finally, with GAs it is helpful if $c$ is a bijection. The important property of bijections as they apply to GAs is that bijections have an inverse, i.e., there is a unique vector $x$ for every string and a unique string for each $x$.
| |
| | | | |
| | + | ----------------------------------------- |
| | + | ----------------------------------------- |
| | | | |
| − | ==Genetic algorithms and their Operators==
| + | $\newcommand*{\longhookrightarrow}{\lhook\joinrel\relbar\joinrel\rightarrow}$ |
| | | | |
| − | Let $H$ be a nonempty set (the individual or search space)
| + | <asy> |
| − | \[{{\left\{{{u}^{i}} \right\}}_{i\ in \mathbb{N}}}\]
| + | size(100,100); |
| − | a sequence in
| + | label(scale(1.7)*'$T(\\Sigma)\hookrightarrow T(\\Sigma,X)$',(0,0)); |
| − | \[{{\mathbb{Z}}^{+}}\]
| + | </asy> |
| − | (the parent populations). | |
| − | \[{{\left\{ {{u}^{'(i)}} \right\}}_{i\in \mathbb{N}}}\]
| |
| − | a sequence in
| |
| − | \[{{\mathbb{Z}}^{+}}\]
| |
| − | (the offspring population sizes), | |
| − | \[\phi:H\to \mathbb{R}\] | |
| − | a fitness function,
| |
| − | \[\iota :\cup_{i=1}^{\infty}{{({{H}^{u}})}^{(i)}}\to\]
| |
| − | {true,false} (the termination criteria),
| |
| − | \[\chi\in\]
| |
| − | {true, false}, r a sequence
| |
| − | \[\left\{{{r}^{(i)}} \right\}\]
| |
| | | | |
| − | Define the collection $\mu$ (the number of individuals) via $H_\mu$. The population transforms are denoted by
| + | <asy> |
| − | \[T:{{H}^{\mu }}\to {{H}^{\mu }}\]
| + | size(220,220); |
| − | where
| |
| − | \[\mu \in \mathbb{N}\ of recombination operators τ(i) : \[X_{r}^{(i)}\ to T(\Omega _{r}^{(i)},T\left( {{H}^{{{u}^{(i)}}}},{{H}^{u{{'}^{(i)}}}} \right)),\]
| |
| − | $m$ a sequence of {m(i)} of mutation operators in mi,
| |
| − | \[X_{m}^{(i)}\to T(\Omega _{m}^{(i)},T\left({{H}^{{{u}^{(i)}}}},{{H}^{u{{'}^{(i)}}}} \right)),\]
| |
| − | $s$ a sequence of {si} selection operators s(i):
| |
| − | \[X_{s}^{(i)}\timesT(H,\mathbb{R})\to T(\Omega _{s}^{(i)},T(({{H}^{u{{'}^{(i)+\chi {{\mu}^{(i)}}}}}}),{{H}^{{{\mu }^{(i+1)}}}})),\]
| |
| − | \[\Theta _{r}^{(i)}\ in X_{r}^{(i)}\]
| |
| − | (the recombination parameters),
| |
| − | \[\Theta _{m}^{(i)}\\in X_{m}^{(i)}\]
| |
| − | (the mutation parameters), and
| |
| − | \[\Theta _{s}^{(i)}\ in X_{s}^{(i)}\]
| |
| − | (the selection parameters).
| |
| | | | |
| − | To account for the cases where populations whose size not equal to their predecessors’, the following expression
| + | import math; |
| − | \[T:{{H}^{\mu}}\to {{H}^{{{\mu }'}}}\]
| |
| − | accommodates populations that contain the same or different individuals. This mapping has the ability to represent all population sizes, genetic operators, and parameters as sequences.
| |
| | | | |
| − | The execution of a GA typically begins by random sampling with replacement from $A^l$. The resulting collection is the initial population, denoted by $P(0)$. In general, a population is a collection
| + | int kmax=40; |
| − | \[P=({{a}_{1}},{{a}_{2}},...,{{a}_{\mu }})\]
| |
| − | of individuals, where
| |
| − | \[{{a}_{i}}\in {{A}^{l}},\]
| |
| − | and populations are treated as $n$-tuples of individuals. The number of individuals ($\mu$) is defined as the population size.
| |
| | | | |
| − | Following upon the work of Lamont and Merkle (Lamont, 1997) and others, the termination criteria and the other genetic operators(GOs)will be defined in more detail.
| + | guide g; |
| | + | for (int k=-kmax; k<=kmax; ++k) { |
| | + | real phi = 0.2*k*pi; |
| | + | real rho = 1; |
| | + | if (k!=0) { |
| | + | rho = sin(phi)/phi; |
| | + | } |
| | + | pair z=rho*expi(phi); |
| | + | g=g..z; |
| | + | } |
| | + | |
| | + | draw (g); |
| | | | |
| − | Since $H$ is a nonempty set,
| + | defaultpen(0.75); |
| − | \[c:{{A}^{l}}\to H,\]
| + | draw ( (0,0)--(1.3,0), dotted, Arrow(SimpleHead,5) ); |
| − | and
| + | dot ( (1,0) ); |
| − | \[f:H\to \mathbb{R},\]
| + | label ( "$a$", (1,0), NE ); |
| − | the fitness scaling function can be defined as
| |
| − | \[{{T}_{s}}:\mathbb{R}\to \mathbb{R}\]
| |
| − | and a related fitness function as
| |
| − | \[\Phi \triangleq {{T}_{s}}\circ f\circ c.\]
| |
| − | In this definition it is understood that the objective function $f$ is determined by the application, while the specification of the decoding function $c[1]$ and the fitness scaling function $T_s$ are design issues.
| |
| | | | |
| − | | + | </asy> |
| − | After initialization, the execution proceeds iteratively. Each iteration consists of an application of one or more GOs. The combined effect of the GOs applied in a particular generation $t\in N$ is a transformation of the current population ''Italic text''P(t) into a new population ''Italic text''P(t+1).
| |
| − | | |
| − | In the population transformation $\mu ,{\mu}'\ in {{\mathbb{Z}}^{+}}$(the parent and offspring population sizes, respectively). A mapping $T:{{H}^{\mu }}\ to {{H}^{{{\mu }'}}}$ is called a population transformation (''Italic text''PT). If $T(P)={P}'$, then ''Italic text''P is the parent population and <sup>Superscript text</sup>''Italic text''P/ the offspring population. If $\mu ={\mu }'$,then it is called the population size.
| |
| − | | |
| − | The ''Italic text''PT resulting from a GO often depends on the outcome of a random experiment. This result is referred to as a random population transformation (''Italic text''RPT or random PT). To define ''Italic text''RPT, let $\mu \in {{\mathbb{Z}}^{+}}$and $\Omega $ be a set (the sample space). A random function $R:\Omega \to T({{H}{\mu }},\bigcup\limits_{{\mu }'\ in {{\mathbb{Z}}^{+}}}^{{}}{{{H}^{{{\mu }'}}}})$ is called a ''Italic text''RPT. The distribution of ''Italic text''PTs resulting from the application of a GO depends on the operator parameters; in other words, a GO maps its parameters to a ''Italic text''RPT.
| |
| − | | |
| − | Now that both the fitness function and ''Italic text''RPT have been defined, let$\mu \in {{\mathbb{Z}}^{+}}$, ''Italic text''X be a set (the parameter space) and $\Omega $ a set. The mapping $\Zeta :X\to T\left( \Omega ,T\left[ {{H}^{\mu }},\bigcup\limits_{{\mu }'\in {{\mathbb{Z}}^{+}}}^{{}}{{{H}^{{{\mu}'}}}} \right] \right)$ is a GO. The set of GOs is denoted as $GAOP\left( H,\mu ,X,\Omega \right)$.
| |
| − | | |
| − | | |
| − | There are three common GOs: recombination,mutation, and selection. These three operators are roughly analogous to their similarly named counterparts in genetics. The application of them in GAs is strictly Darwin-like in nature, i.e., “survival of the fittest.”
| |
| − | | |
| − | For the recombination operator let $r\in GAOP\left( H,\mu ,X,\Omega \right)$. If there exists $P\in {{H}^{\mu }},\Theta \in X$, and $\omega \in \Omega $, such that one individual in the offspring population ${{r}_{\Theta }}\left( P \right)$ depends on more than one individual of P,then r is referred to as a recombination operator.
| |
| − | | |
| − | For the mutation operator let $m\in GAOP\left( H,\mu ,X,\Omega\right)$. If for every $P\in {{H}^{\mu }}$, for every $\Theta \in X$, for every $\omega\in \Omega $, and if each individual in the offspring population ${{m}_{\Theta}}\left( P \right)$ depends on at most one individual of P, then m is called a mutation operator.
| |
| − | | |
| − | Finally, for the selection operator let $s\in EVOP\left( H,\mu ,X\times T\left(H,\mathbb{R}),\Omega \right) \right)$. If $P\in {{H}^{\mu }}$,$\Theta \in X$,$\Phi :H\to\mathbb{R}$in all cases, and satisfies $a\in {{s}_{\left( \Theta ,\Phi \right)}}(P)\Rightarrow a\in P$, then s is a selection operator.
| |
| − | | |
| − | | |
| − | | |
| − | | |
| − | | |
| − | | |
| − | | |
| − | '''Bold text'''Endnotes
| |
| − | | |
| − | [1] If the domain of c is total, i.e., the domain of c is all of A I, c is called a decoding function. The mapping of c is not necessarily surjective. The range of c determines the subset of Al available for exploration by the evolutionary algorithm.
| |