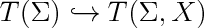|
|
| (301 intermediate revisions by the same user not shown) |
| Line 1: |
Line 1: |
| − | ''Also: analytic measurable space''
| + | <ref> [http://hea-www.harvard.edu/AstroStat http://hea-www.harvard.edu/AstroStat]; <nowiki> http://www.incagroup.org </nowiki>; <nowiki> http://astrostatistics.psu.edu </nowiki> </ref> |
| | | | |
| − | [[:Category:Descriptive set theory]]
| + | ====Notes==== |
| − | [[:Category:Classical measure theory]]
| + | <references /> |
| | | | |
| − | {{User:Rehmann/sandbox/MSC|03E15|28A05,54H05}}
| + | ------------------------------------------- |
| | | | |
| − | $ \newcommand{\R}{\mathbb R}
| |
| − | \newcommand{\C}{\mathbb C}
| |
| − | \newcommand{\Om}{\Omega}
| |
| − | \newcommand{\A}{\mathcal A}
| |
| − | \newcommand{\B}{\mathcal B}
| |
| − | \newcommand{\P}{\mathbf P} $
| |
| − | A [[measurable space|Borel space]] is called '''analytic''' if it is [[Measurable space#separated|countably separated]] and [[Measurable space#isomorphic|isomorphic]] to a [[Measurable space#quotient space|quotient space]] of a [[Standard Borel space|standard]] Borel space.
| |
| | | | |
| − | This is one out of several equivalent definitions (see below).
| + | {| |
| | + | | A || B || C |
| | + | |- |
| | + | | X || Y || Z |
| | + | |} |
| | | | |
| − | Finite and countable analytic Borel spaces are trivial: all subsets are measurable. Uncountable
| |
| − | analytic Borel spaces are of [[Continuum, cardinality of the|cardinality continuum]]. Some, but not all, of them are standard; these are mutually isomorphic. Some additional (to [[ZFC]]) set-theoretic axioms imply that all nonstandard analytic Borel spaces are mutually isomorphic (see [1, Sect. 26.D]).
| |
| | | | |
| − | ''Non-example.'' The [[quotient group]] $\R/\Q$ (real numbers modulo rational numbers, additive) may be thought of as a quotient measurable space, $\R$ being endowed with its Borel σ-algebra. Then $\R/\Q$ is a quotient space of a standard Borel space, but not an analytic Borel space, because it is not countably separated. (See [2, Sect. 5].)
| |
| | | | |
| − | ====Relations to analytic sets====
| + | ----------------------------------------- |
| | + | ----------------------------------------- |
| | | | |
| − | A subset of a standard Borel (or just countably separated measurable) space is called ''analytic'' if it is the image of a standard Borel space under a Borel map. (See [1, Sect. 14.A].)
| + | $\newcommand*{\longhookrightarrow}{\lhook\joinrel\relbar\joinrel\rightarrow}$ |
| | | | |
| − | As every subset of a measurable space, an analytic set is itself a measurable space (a
| + | <asy> |
| − | [[Measurable space#subspace|subspace]] of the given space).
| + | size(100,100); |
| | + | label(scale(1.7)*'$T(\\Sigma)\hookrightarrow T(\\Sigma,X)$',(0,0)); |
| | + | </asy> |
| | | | |
| − | '''Definition 2''' (equivalent).
| + | <asy> |
| − | A Borel space is called ''analytic'' if it is isomorphic to an analytic set.
| + | size(220,220); |
| | | | |
| − | Equivalence of the two definitions follows from the [[Standard Borel space#Blackwell-Mackey theorem|Blackwell-Mackey theorem]] and the following simple fact: every countably separated measurable space admits a one-to-one measurable map to a standard Borel space.
| + | import math; |
| | | | |
| − | See [1, Sect. 25.A], [2, Sect. 4] for these, and some other, definitions of analytic sets and spaces.
| + | int kmax=40; |
| | | | |
| − | ====Measurable injections==== | + | guide g; |
| | + | for (int k=-kmax; k<=kmax; ++k) { |
| | + | real phi = 0.2*k*pi; |
| | + | real rho = 1; |
| | + | if (k!=0) { |
| | + | rho = sin(phi)/phi; |
| | + | } |
| | + | pair z=rho*expi(phi); |
| | + | g=g..z; |
| | + | } |
| | + | |
| | + | draw (g); |
| | | | |
| − | Several [[Standard Borel space#Measurable injections|results on standard Borel spaces]] generalize to analytic Borel spaces (see [2, Sect. 4]).
| + | defaultpen(0.75); |
| | + | draw ( (0,0)--(1.3,0), dotted, Arrow(SimpleHead,5) ); |
| | + | dot ( (1,0) ); |
| | + | label ( "$a$", (1,0), NE ); |
| | | | |
| − | '''Theorem 1a.''' If a bijective map between analytic Borel spaces is measurable then the inverse map is also measurable.
| + | </asy> |
| − | | |
| − | '''Theorem 1b.''' If σ-algebras $\A$, $\B$ on $X$ are such that $\A\subset\B$ and $(X,\A)$, $(X,\B)$ are analytic then $\A=\B$.
| |
| − | | |
| − | ''Example.'' The real line with the Lebesgue σ-algebra is not analytic (by Theorem 1b).
| |
| − | | |
| − | '''Theorem 2a.''' If a bijective map from an analytic Borel space to a countably separated measurable space is measurable then the inverse map is also measurable.
| |
| − | | |
| − | '''Theorem 2b.''' If σ-algebras $\A$, $\B$ on $X$ are such that $\A\subset\B$, $(X,\A)$ is countably separated and $(X,\B)$ is analytic then $\A=\B$.
| |
| − | | |
| − | '''Theorem 2c.''' If $(X,\A)$ is an analytic Borel space then $\A$ is generated by every at most countable [[Measurable space#separating|separating]] subset of $\A$. (See [3, Sect. 3].
| |
| − | | |
| − | ====References====
| |
| − | {|
| |
| − | |valign="top"|[1]|| Alexander S. Kechris, "Classical descriptive set theory", Springer-Verlag (1995). {{MR|1321597}} {{ZBL|0819.04002}}
| |
| − | |-
| |
| − | |valign="top"|[2]|| George W. Mackey, "Borel structure in groups and their duals", ''Trans. Amer. Math. Soc.'' '''85''' (1957), 134–165. {{MR|0089999}} {{ZBL|0082.11201}}
| |
| − | |-
| |
| − | |valign="top"|[3]|| S.M. Srivastava, "A course on Borel sets", Springer-Verlag (1998). {{MR|1619545}} {{ZBL|0903.28001}}
| |
| − | |}
| |