Difference between revisions of "Partial differential equations, property C for"
m (semi-texifed) |
m (semi-texified) |
||
| Line 15: | Line 15: | ||
Is property $C$ generic for a pair of formal partial differential operators $L_1$ and $L_2$? | Is property $C$ generic for a pair of formal partial differential operators $L_1$ and $L_2$? | ||
| − | For the operators with constant coefficients, a necessary and sufficient condition is given in [[#References|[a10]]] for a pair $\{L_1,L_2\}$ to have property $C$. For such operators it turns out that property $C$ is generic and holds or fails to hold simultaneously for all $p\in[1,\infty)$: Assume $a_{jm}(x)=a_{jm}=\text{const}$. Denote $L_m(z):=\sum^{J}_{|j|=0}a_{jm}z^j$, $z\in\textbf{C}^n$. Note that | + | For the operators with constant coefficients, a necessary and sufficient condition is given in [[#References|[a10]]] for a pair $\{L_1,L_2\}$ to have property $C$. For such operators it turns out that property $C$ is generic and holds or fails to hold simultaneously for all $p\in[1,\infty)$: Assume $a_{jm}(x)=a_{jm}=\text{const}$. Denote $L_m(z):=\sum^{J}_{|j|=0}a_{jm}z^j$, $z\in\textbf{C}^n$. Note that $L_m(e^{zx})=e^{zx}L_m(z)$, $z.x:=\sum^n_{j=1}z_jx_j$. |
| − | Therefore | + | Therefore $e^{zx}\in\widetilde{N}_m$ if and only if $L_m(z)=0$. |
Define the algebraic varieties (cf. also [[Algebraic variety|Algebraic variety]]) | Define the algebraic varieties (cf. also [[Algebraic variety|Algebraic variety]]) | ||
| − | + | \begin{equation}\mathcal{L}_m:=\{z:z\in\mathbf{C}^n,L_m(z)=0\}.\end{equation} | |
| − | One says that | + | One says that $\mathcal{L}_1$ is transversal to $\mathcal{L}_2$, and writes $\mathcal{L}_1\nparallel\mathcal{L}_2$, if and only if there exist a point $\zeta\in\mathcal{L}_1$ and a point $\xi\in\mathcal{L}_2$ such that the tangent space $T_1$ to $\mathcal{L}_1$ (in $\mathbf{C}^n)$ at the point $\zeta$ and the tangent space $T_2$ to $\mathcal{L}_2$ at the point $\xi$ are transversal (cf. [[Transversality|Transversality]]). |
| − | The following result is proved in [[#References|[a1]]]: The pair | + | The following result is proved in [[#References|[a1]]]: The pair $\{L_1,L_2\}$ of formal partial differential operators with constant coefficients has property $C$ if and only if $\mathcal{L}_1\nparallel\mathcal{L}_2$. |
| − | Thus, property | + | Thus, property $C$ fails to hold for a pair $\{L_1,L_2\}$ of formal differential operators with constant coefficients if and only if the variety $\mathcal{L}_1\cup\mathcal{L}_2$ is a union of parallel hyperplanes in $\mathbf{C}^n$. |
| − | Therefore, property | + | Therefore, property $C$ for partial differential operators with constant coefficients is generic. |
| − | If | + | If $L_1=L_2=L$ and the pair $\{L,L\}$ has property $C$, then one says that $L$ has property $C$. |
==Examples.== | ==Examples.== | ||
| − | Let | + | Let $n\geq 2$, $L=\nabla^2:=\sum^n_{j=1}$. Then $. It is easy to check that there are points <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130030/p13003079.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130030/p13003080.png" /> at which the tangent hyperplanes to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130030/p13003081.png" /> are not parallel. Thus <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130030/p13003082.png" /> has property <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130030/p13003083.png" />. This means that the set of products of harmonic functions in a bounded domain <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130030/p13003084.png" /> is complete in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130030/p13003085.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130030/p13003086.png" /> (cf. also [[Harmonic function|Harmonic function]]). Similarly one checks that the operators |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130030/p13003087.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130030/p13003087.png" /></td> </tr></table> | ||
Revision as of 15:37, 26 April 2021
Property $C$ stands for "completeness" of the set of products of solutions to homogeneous linear partial differential equations. It was introduced in [a1] and used in [a2], [a3], [a4], [a5], [a6], [a7], [a8], [a9], [a10], [a11], [a12], [a13] as a powerful tool for proving uniqueness results for many multi-dimensional inverse problems, in particular, inverse scattering problems (cf. also Inverse scattering, multi-dimensional case).
Let $D$ be a bounded domain in $\textbf{R}^n$, $n\geq 2$, let $L_mu(x):=\sum^{J}_{|j|=0}a_{jm}(x)D^ju(x)$, where $j$ is a multi-index, $D^ju=\partial^{|j|}u/\partial x_1^{j_{1}}...\partial x_n^{j_{n}}$, derivatives being understood in the distributional sense, the $a_{jm}(x)$, $m=1,2$, are certain $L^{\infty}(D)$ functions, $N_m:=\{w:L_mw=0\text{in}D\}$ is the null-space of the formal differential operator $L_m$, and the equation $L_mw=0$ is understood in the distributional sense.
Consider the subsets $\widetilde{N}_1\in N_2$ and $\widetilde{N}_2\in N_n$ for which the products $w_1w_2$ are defined, $w_1\in\widetilde{N}_1$, $w_2\in\widetilde{N}_2$.
The pair $\{L_1,L_2\}$ has property $C_p$ if and only if the set $\{w_1w_2\}_{\forall w_{m}\in\widetilde{N}_{m}}$ is total (complete) in $L^p(D)$, ($p\geq 1$ is fixed), that is, if $f(x)\in L^p(D)$ and
\begin{equation}\int_{D}f(x)w_1(x)w_2(x)dx=0,\\\forall w_1\in\widetilde{N}_1,\forall w_2\in\widetilde{N}_2,\end{equation}
then $f(x)\equiv 0$.
By property $C$ one often means property $C_2$ or $C_p$ with any fixed $p\geq1$.
Is property $C$ generic for a pair of formal partial differential operators $L_1$ and $L_2$?
For the operators with constant coefficients, a necessary and sufficient condition is given in [a10] for a pair $\{L_1,L_2\}$ to have property $C$. For such operators it turns out that property $C$ is generic and holds or fails to hold simultaneously for all $p\in[1,\infty)$: Assume $a_{jm}(x)=a_{jm}=\text{const}$. Denote $L_m(z):=\sum^{J}_{|j|=0}a_{jm}z^j$, $z\in\textbf{C}^n$. Note that $L_m(e^{zx})=e^{zx}L_m(z)$, $z.x:=\sum^n_{j=1}z_jx_j$.
Therefore $e^{zx}\in\widetilde{N}_m$ if and only if $L_m(z)=0$.
Define the algebraic varieties (cf. also Algebraic variety)
\begin{equation}\mathcal{L}_m:=\{z:z\in\mathbf{C}^n,L_m(z)=0\}.\end{equation}
One says that $\mathcal{L}_1$ is transversal to $\mathcal{L}_2$, and writes $\mathcal{L}_1\nparallel\mathcal{L}_2$, if and only if there exist a point $\zeta\in\mathcal{L}_1$ and a point $\xi\in\mathcal{L}_2$ such that the tangent space $T_1$ to $\mathcal{L}_1$ (in $\mathbf{C}^n)$ at the point $\zeta$ and the tangent space $T_2$ to $\mathcal{L}_2$ at the point $\xi$ are transversal (cf. Transversality).
The following result is proved in [a1]: The pair $\{L_1,L_2\}$ of formal partial differential operators with constant coefficients has property $C$ if and only if $\mathcal{L}_1\nparallel\mathcal{L}_2$.
Thus, property $C$ fails to hold for a pair $\{L_1,L_2\}$ of formal differential operators with constant coefficients if and only if the variety $\mathcal{L}_1\cup\mathcal{L}_2$ is a union of parallel hyperplanes in $\mathbf{C}^n$.
Therefore, property $C$ for partial differential operators with constant coefficients is generic.
If $L_1=L_2=L$ and the pair $\{L,L\}$ has property $C$, then one says that $L$ has property $C$.
Examples.
Let $n\geq 2$, $L=\nabla^2:=\sum^n_{j=1}$. Then $. It is easy to check that there are points 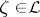 and
and 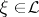 at which the tangent hyperplanes to
at which the tangent hyperplanes to 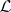 are not parallel. Thus
are not parallel. Thus 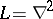 has property
has property 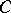 . This means that the set of products of harmonic functions in a bounded domain
. This means that the set of products of harmonic functions in a bounded domain 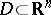 is complete in
is complete in 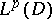 ,
, 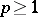 (cf. also Harmonic function). Similarly one checks that the operators
(cf. also Harmonic function). Similarly one checks that the operators
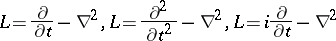 |
have property 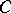 .
.
Numerous applications of property 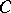 to inverse problems can be found in [a1].
to inverse problems can be found in [a1].
Property 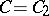 holds for a pair of Schrödinger operators with potentials
holds for a pair of Schrödinger operators with potentials  ,
, 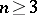 , where
, where  is the set of
is the set of 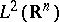 functions with compact support{} (cf. also Schrödinger equation).
functions with compact support{} (cf. also Schrödinger equation).
If 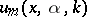 ,
, 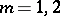 ,
, 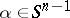 ,
,  ,
,  is the unit sphere in
is the unit sphere in 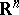 , are the scattering solutions corresponding to the Schrödinger operators
, are the scattering solutions corresponding to the Schrödinger operators 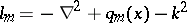 ,
,  ,
, 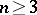 , then the set of products
, then the set of products 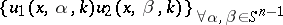 ,
,  is fixed, is complete in
is fixed, is complete in 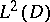 , where
, where 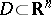 is an arbitrary fixed bounded domain [a1]. The set
is an arbitrary fixed bounded domain [a1]. The set 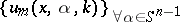 , where
, where 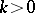 is fixed, is total in the set
is fixed, is total in the set  , where
, where 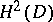 is the Sobolev space [a1].
is the Sobolev space [a1].
References
| [a1] | A.G. Ramm, "Multidimensional inverse scattering problems" , Longman/Wiley (1992) |
| [a2] | A.G. Ramm, "Scattering by obstacles" , Reidel (1986) |
| [a3] | A.G. Ramm, "Completeness of the products of solutions to PDE and uniqueness theorems in inverse scattering" Inverse Probl. , 3 (1987) pp. L77–L82 |
| [a4] | A.G. Ramm, "Multidimensional inverse problems and completeness of the products of solutions to PDE" J. Math. Anal. Appl. , 134 : 1 (1988) pp. 211–253 (Also: 139 (1989), 302) |
| [a5] | A.G. Ramm, "Recovery of the potential from fixed energy scattering data" Inverse Probl. , 4 (1988) pp. 877–886 (Also: 5 (1989), 255) |
| [a6] | A.G. Ramm, "Multidimensional inverse problems: Uniqueness theorems" Appl. Math. Lett. , 1 : 4 (1988) pp. 377–380 |
| [a7] | A.G. Ramm, "Multidimensional inverse scattering problems and completeness of the products of solutions to homogeneous PDE" Z. Angew. Math. Mech. , 69 : 4 (1989) pp. T13–T22 |
| [a8] | A.G. Ramm, "Property C and uniqueness theorems for multidimensional inverse spectral problem" Appl. Math. Lett. , 3 (1990) pp. 57–60 |
| [a9] | A.G. Ramm, "Completeness of the products of solutions of PDE and inverse problems" Inverse Probl. , 6 (1990) pp. 643–664 |
| [a10] | A.G. Ramm, "Necessary and sufficient condition for a PDE to have property C" J. Math. Anal. Appl. , 156 (1991) pp. 505–509 |
| [a11] | A.G. Ramm, "Property C and inverse problems" , ICM-90 Satellite Conf. Proc. Inverse Problems in Engineering Sci. , Springer (1991) pp. 139–144 |
| [a12] | A.G. Ramm, "Stability estimates in inverse scattering" Acta Applic. Math. , 28 : 1 (1992) pp. 1–42 |
| [a13] | A.G. Ramm, "Stability of solutions to inverse scattering problems with fixed-energy data" Rend. Sem. Mat. e Fisico (2001) pp. 135–211 |
Partial differential equations, property C for. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Partial_differential_equations,_property_C_for&oldid=51703