Namespaces
Variants
Actions

Difference between revisions of "Trivector"

From Encyclopedia of Mathematics
Jump to: navigation, search
m (tex encoded by computer)
m (Undo revision 49041 by Ulf Rehmann (talk))
Tag: Undo
Line 1: Line 1:
−
<!--
+
An ordered family <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t094/t094320/t0943201.png" /> of three vectors <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t094/t094320/t0943202.png" /> in an affine space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t094/t094320/t0943203.png" />, emanating from a common origin. A trivector is set equal to zero if the vectors defining it are coplanar (linearly dependent). A non-zero trivector determines the three-dimensional space supporting it. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t094/t094320/t0943204.png" /> has finite dimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t094/t094320/t0943205.png" /> and if in some basis <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t094/t094320/t0943206.png" /> the vectors are
−
t0943201.png
 
−
$#A+1 = 24 n = 0
 
−
$#C+1 = 24 : ~/encyclopedia/old_files/data/T094/T.0904320 Trivector
 
−
Automatically converted into TeX, above some diagnostics.
 
−
Please remove this comment and the {{TEX|auto}} line below,
 
−
if TeX found to be correct.
 
−
-->
 
  
−
{{TEX|auto}}
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t094/t094320/t0943207.png" /></td> </tr></table>
−
{{TEX|done}}
 
  
−
An ordered family  $  [ \mathbf u , \mathbf v , \mathbf w ] $
+
then the quantities
−
of three vectors  $  \mathbf u , \mathbf v , \mathbf w $
 
−
in an affine space  $  A $,
 
−
emanating from a common origin. A trivector is set equal to zero if the vectors defining it are coplanar (linearly dependent). A non-zero trivector determines the three-dimensional space supporting it. If  $  A $
 
−
has finite dimension  $  n $
 
−
and if in some basis  $  e = ( \mathbf e _ {1} \dots \mathbf e _ {n} ) $
 
−
the vectors are
 
  
−
$$
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t094/t094320/t0943208.png" /></td> </tr></table>
−
\mathbf u  = \sum _ {i = 1 } ^ { n }  u  ^ {i} \mathbf e _ {i} ,\ \
 
−
\mathbf v  = \sum _ {i = 1 } ^ { n }  v  ^ {i} \mathbf e _ {i} ,\ \
 
−
\mathbf w  = \sum _ {i = 1 } ^ { n }  w  ^ {i} \mathbf e _ {i} ,
 
−
$$
 
  
−
then the quantities
+
are called the coordinates of the trivector <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t094/t094320/t0943209.png" /> with respect to the basis <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t094/t094320/t09432010.png" />. These coordinates are skew-symmetric with respect to any pair of indices; under a change of basis in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t094/t094320/t09432011.png" />, they transform like coordinates of a triply-contravariant tensor. Of these coordinates, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t094/t094320/t09432012.png" /> are essential. Two trivectors are said to be equal if their coordinates are equal in any basis of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t094/t094320/t09432013.png" />. A class of equal trivectors is called a free trivector.
  
−
$$
+
In the presence of a scalar product in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t094/t094320/t09432014.png" />, several metric concepts of vector algebra can be applied to trivectors. The measure of a trivector <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t094/t094320/t09432015.png" /> is the three-dimensional volume of the parallelopipedon formed by the set of ends of vectors of the form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t094/t094320/t09432016.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t094/t094320/t09432017.png" />, emanating from a common origin. In the case when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t094/t094320/t09432018.png" />, the measure of the trivector is equal to the triple scalar product of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t094/t094320/t09432019.png" />. The scalar product of two trivectors is the number equal to the product of the measures of the factors by the cosine of the angle between the planes supporting them. The scalar product is a bilinear form of the coordinates of the factors. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t094/t094320/t09432020.png" />, then the trivector <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t094/t094320/t09432021.png" /> can be identified with a vector of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t094/t094320/t09432022.png" />, called the [[Vector product|vector product]] of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t094/t094320/t09432023.png" />.
−
a ^ {ijk}  = \
 
−
\left |
 
  
−
are called the coordinates of the trivector $  [ \mathbf u , \mathbf v , \mathbf w ] $
+
A trivector in tensor calculus is any contravariant skew-symmetric tensor of valency 3 (that is, a tensor of type <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t094/t094320/t09432024.png" />). Each such tensor can be represented as the sum of several tensors to which correspond trivectors with distinct supporting planes.
−
with respect to the basis  $  e $.
 
−
These coordinates are skew-symmetric with respect to any pair of indices; under a change of basis in  $  A $,  
 
−
they transform like coordinates of a triply-contravariant tensor. Of these coordinates,  $  n ( n - 1) ( n - 2)/6 $
 
−
are essential. Two trivectors are said to be equal if their coordinates are equal in any basis of $  A $.
 
−
A class of equal trivectors is called a free trivector.
 
  
−
In the presence of a scalar product in  $  A $,
+
See also [[Bivector|Bivector]]; [[Exterior product|Exterior product]]; [[Poly-vector|Poly-vector]]; [[Plücker coordinates|Plücker coordinates]].
−
several metric concepts of vector algebra can be applied to trivectors. The measure of a trivector  $  [ \mathbf u , \mathbf v , \mathbf w ] $
 
−
is the three-dimensional volume of the parallelopipedon formed by the set of ends of vectors of the form  $  \mathbf h = x \mathbf u + y \mathbf v + z \mathbf w $,
 
−
where  $  0 \leq  x, y, z \leq  1 $,
 
−
emanating from a common origin. In the case when  $  \mathop{\rm dim}  A = 3 $,
 
−
the measure of the trivector is equal to the triple scalar product of  $  \mathbf u , \mathbf v , \mathbf w $.
 
−
The scalar product of two trivectors is the number equal to the product of the measures of the factors by the cosine of the angle between the planes supporting them. The scalar product is a bilinear form of the coordinates of the factors. If  $  \mathop{\rm dim}  A = 4 $,
 
−
then the trivector  $  [ \mathbf u , \mathbf v , \mathbf w ] $
 
−
can be identified with a vector of  $  A $,
 
−
called the [[Vector product|vector product]] of  $  \mathbf u , \mathbf v , \mathbf w $.
 
  
−
A trivector in tensor calculus is any contravariant skew-symmetric tensor of valency 3 (that is, a tensor of type  $  ( 3, 0) $).
 
−
Each such tensor can be represented as the sum of several tensors to which correspond trivectors with distinct supporting planes.
 
  
−
See also [[Bivector|Bivector]]; [[Exterior product|Exterior product]]; [[Poly-vector|Poly-vector]]; [[Plücker coordinates|Plücker coordinates]].
 
  
 
====Comments====
 
====Comments====
 +
  
 
====References====
 
====References====
 
<table><TR><TD valign="top">[a1]</TD> <TD valign="top">  J.A. Schouten,  "Ricci-calculus. An introduction to tensor analysis and its geometrical applications" , Springer  (1954)  pp. §I.7  (Translated from German)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top">  D. Hestenes,  G. Sobszyk,  "Clifford algebra to geometric calculus" , Reidel  (1984)  pp. 4</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top">  R. Sauer (ed.)  I. Szabó (ed.) , ''Mathematische Hilfsmittel des Ingenieurs'' , '''III''' , Springer  (1970)  pp. 174</TD></TR></table>
 
<table><TR><TD valign="top">[a1]</TD> <TD valign="top">  J.A. Schouten,  "Ricci-calculus. An introduction to tensor analysis and its geometrical applications" , Springer  (1954)  pp. §I.7  (Translated from German)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top">  D. Hestenes,  G. Sobszyk,  "Clifford algebra to geometric calculus" , Reidel  (1984)  pp. 4</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top">  R. Sauer (ed.)  I. Szabó (ed.) , ''Mathematische Hilfsmittel des Ingenieurs'' , '''III''' , Springer  (1970)  pp. 174</TD></TR></table>

Revision as of 14:53, 7 June 2020

An ordered family 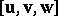of three vectors 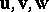in an affine space 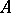, emanating from a common origin. A trivector is set equal to zero if the vectors defining it are coplanar (linearly dependent). A non-zero trivector determines the three-dimensional space supporting it. If 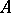has finite dimension and if in some basis 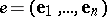the vectors are

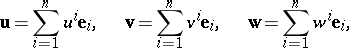then the quantities

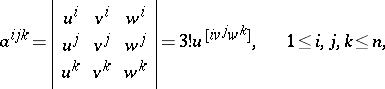are called the coordinates of the trivector 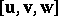with respect to the basis . These coordinates are skew-symmetric with respect to any pair of indices; under a change of basis in 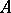, they transform like coordinates of a triply-contravariant tensor. Of these coordinates, 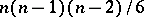are essential. Two trivectors are said to be equal if their coordinates are equal in any basis of 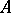. A class of equal trivectors is called a free trivector.

In the presence of a scalar product in 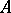, several metric concepts of vector algebra can be applied to trivectors. The measure of a trivector 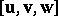is the three-dimensional volume of the parallelopipedon formed by the set of ends of vectors of the form 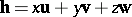, where 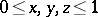, emanating from a common origin. In the case when 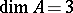, the measure of the trivector is equal to the triple scalar product of 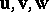. The scalar product of two trivectors is the number equal to the product of the measures of the factors by the cosine of the angle between the planes supporting them. The scalar product is a bilinear form of the coordinates of the factors. If 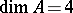, then the trivector 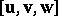can be identified with a vector of , called the vector product of .

A trivector in tensor calculus is any contravariant skew-symmetric tensor of valency 3 (that is, a tensor of type 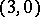). Each such tensor can be represented as the sum of several tensors to which correspond trivectors with distinct supporting planes.

See also Bivector; Exterior product; Poly-vector; Plücker coordinates.


Comments

References

[a1] J.A. Schouten, "Ricci-calculus. An introduction to tensor analysis and its geometrical applications" , Springer (1954) pp. §I.7 (Translated from German)
[a2] D. Hestenes, G. Sobszyk, "Clifford algebra to geometric calculus" , Reidel (1984) pp. 4
[a3] R. Sauer (ed.) I. Szabó (ed.) , Mathematische Hilfsmittel des Ingenieurs , III , Springer (1970) pp. 174
How to Cite This Entry:
Trivector. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Trivector&oldid=49041
This article was adapted from an original article by L.P. Kuptsov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article
Retrieved from "https://encyclopediaofmath.org/index.php?title=Trivector&oldid=49483"