Namespaces
Variants
Actions

Difference between revisions of "Transfer function"

From Encyclopedia of Mathematics
Jump to: navigation, search
m (tex encoded by computer)
m (Undo revision 49008 by Ulf Rehmann (talk))
Tag: Undo
Line 1: Line 1:
−
<!--
 
−
t0936501.png
 
−
$#A+1 = 23 n = 0
 
−
$#C+1 = 23 : ~/encyclopedia/old_files/data/T093/T.0903650 Transfer function
 
−
Automatically converted into TeX, above some diagnostics.
 
−
Please remove this comment and the {{TEX|auto}} line below,
 
−
if TeX found to be correct.
 
−
-->
 
−
 
−
{{TEX|auto}}
 
−
{{TEX|done}}
 
−
 
 
''for a linear stationary control system (an automatic control system)''
 
''for a linear stationary control system (an automatic control system)''
  
−
The [[Laplace transform|Laplace transform]] of the response to a unit pulse function (delta-function) $  \delta ( t) $
+
The [[Laplace transform|Laplace transform]] of the response to a unit pulse function (delta-function) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093650/t0936501.png" /> with zero conditions at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093650/t0936502.png" /> (this response is called the weighting function, the pulse transfer function or the pulse characteristic). An equivalent definition is that the transfer function is the ratio of the Laplace transforms (see [[Operational calculus|Operational calculus]]) for the output and input signals with zero initial data. The transfer function is a rational-fractional function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093650/t0936503.png" /> of the complex variable <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093650/t0936504.png" />; it is the coefficient in the linear relation
−
with zero conditions at $  t= 0 $(
 
−
this response is called the weighting function, the pulse transfer function or the pulse characteristic). An equivalent definition is that the transfer function is the ratio of the Laplace transforms (see [[Operational calculus|Operational calculus]]) for the output and input signals with zero initial data. The transfer function is a rational-fractional function $  W( p) $
 
−
of the complex variable $  p $;  
 
−
it is the coefficient in the linear relation
 
  
−
$$ \tag{1 }
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093650/t0936505.png" /></td> <td valign="top" style="width:5%;text-align:right;">(1)</td></tr></table>
−
Y( p)  = W( p) U( p),
 
−
$$
 
  
−
relating the Laplace transform $  U( p) $
+
relating the Laplace transform <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093650/t0936506.png" /> of the input of the system (the action, the control) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093650/t0936507.png" /> and the Laplace transform <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093650/t0936508.png" /> of the output (response, reaction) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093650/t0936509.png" /> with zero initial conditions. In control theory, relation (1) is represented graphically as:
−
of the input of the system (the action, the control) $  u( t) $
 
−
and the Laplace transform $  Y( p) $
 
−
of the output (response, reaction) $  y( t) $
 
−
with zero initial conditions. In control theory, relation (1) is represented graphically as:
 
  
−
$$
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093650/t09365010.png" /></td> </tr></table>
−
\rightarrow ^ { u }  \  W( p) \  \rightarrow ^ { y }  .
 
−
$$
 
  
 
For example, let the control system be described by a linear ordinary differential equation with constant coefficients:
 
For example, let the control system be described by a linear ordinary differential equation with constant coefficients:
  
−
$$ \tag{2 }
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093650/t09365011.png" /></td> <td valign="top" style="width:5%;text-align:right;">(2)</td></tr></table>
−
\sum _ { i= } 0 ^ { n }  a _ {i} y  ^ {(} i)  = \sum _ { j= } 0 ^ { m }  b _ {j} u  ^ {(} j)
 
−
,\ \
 
−
a _ {n} = 1
 
−
$$
 
  
−
(in an actual system, $  m \leq  n $
+
(in an actual system, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093650/t09365012.png" /> usually). Then
−
usually). Then
 
  
−
$$ \tag{3 }
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093650/t09365013.png" /></td> <td valign="top" style="width:5%;text-align:right;">(3)</td></tr></table>
−
W( p)  =
 
−
\frac{b _ {m} p  ^ {m} + b _ {m-} 1 p  ^ {m-} 1 + \dots + b _ {0} }{p  ^ {n} + a _ {n-} 1 p  ^ {n-} 1 + \dots + a _ {0} }
 
−
.
 
−
$$
 
  
−
The same expression can be obtained if one uses the operator form of (2) and the differentiation operator $  p $,
+
The same expression can be obtained if one uses the operator form of (2) and the differentiation operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093650/t09365014.png" />,
  
−
$$
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093650/t09365015.png" /></td> </tr></table>
−
A( p) y  = B( p) u,
 
−
$$
 
  
−
to define the transfer function as the ratio of the input operator $  B( p) $
+
to define the transfer function as the ratio of the input operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093650/t09365016.png" /> to the eigenoperator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093650/t09365017.png" />; the transfer function (3) of (2) has the following interpretation: If one selects the control <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093650/t09365018.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093650/t09365019.png" /> is a complex number such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093650/t09365020.png" />, then the linear inhomogeneous equation (2) has the particular solution <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093650/t09365021.png" />.
−
to the eigenoperator $  A( p) $;  
 
−
the transfer function (3) of (2) has the following interpretation: If one selects the control $  u = e  ^ {st} $,  
 
−
where $  s $
 
−
is a complex number such that $  A( s) \neq 0 $,  
 
−
then the linear inhomogeneous equation (2) has the particular solution $  y = W( s) e  ^ {st} $.
 
  
 
The transfer function should not be confused with the step response, which is the response of the system to the unit step function:
 
The transfer function should not be confused with the step response, which is the response of the system to the unit step function:
  
−
$$
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093650/t09365022.png" /></td> </tr></table>
−
u( t)  =  \left \{
 
  
 
with zero initial conditions.
 
with zero initial conditions.
  
−
The transfer function is one of the basic concepts in the theory of linear stationary control systems. It is independent of the control actions imposed on the system and is governed only by the parameters of the system itself, thus providing a dynamical characteristic itself. The function $  W( i \omega ) $
+
The transfer function is one of the basic concepts in the theory of linear stationary control systems. It is independent of the control actions imposed on the system and is governed only by the parameters of the system itself, thus providing a dynamical characteristic itself. The function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093650/t09365023.png" /> of a pure-imaginary argument plays a particular part in control theory; it is called the amplitude-phase, or frequency, characteristic. The concept of a transfer function has been extended also to linear control systems of other types (matrix, non-stationary, discrete, with distributed parameters, etc.).
−
of a pure-imaginary argument plays a particular part in control theory; it is called the amplitude-phase, or frequency, characteristic. The concept of a transfer function has been extended also to linear control systems of other types (matrix, non-stationary, discrete, with distributed parameters, etc.).
 
  
 
====References====
 
====References====
 
<table><TR><TD valign="top">[1]</TD> <TD valign="top">  Ya.N. Roitenberg,  "Automatic control" , Moscow  (1978)  (In Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> , ''Mathematical foundations of automatic control theory'' , Moscow  (1971)  (In Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top">  R.E. Kalman,  P.L. Falb,  M.A. Arbib,  "Topics in mathematical systems theory" , McGraw-Hill  (1969)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top">  A.G. Butkovskii,  "Characteristics of systems with distributed parameters: a handbook" , Moscow  (1979)  (In Russian)</TD></TR></table>
 
<table><TR><TD valign="top">[1]</TD> <TD valign="top">  Ya.N. Roitenberg,  "Automatic control" , Moscow  (1978)  (In Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> , ''Mathematical foundations of automatic control theory'' , Moscow  (1971)  (In Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top">  R.E. Kalman,  P.L. Falb,  M.A. Arbib,  "Topics in mathematical systems theory" , McGraw-Hill  (1969)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top">  A.G. Butkovskii,  "Characteristics of systems with distributed parameters: a handbook" , Moscow  (1979)  (In Russian)</TD></TR></table>
 +
 +
  
 
====Comments====
 
====Comments====
 +
  
 
====References====
 
====References====
 
<table><TR><TD valign="top">[a1]</TD> <TD valign="top">  H. Kwakernaak,  R. Sivan,  "Linear optimal control systems" , Wiley (Interscience)  (1972)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top">  T. Kailath,  "Linear systems" , Prentice-Hall  (1980)</TD></TR></table>
 
<table><TR><TD valign="top">[a1]</TD> <TD valign="top">  H. Kwakernaak,  R. Sivan,  "Linear optimal control systems" , Wiley (Interscience)  (1972)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top">  T. Kailath,  "Linear systems" , Prentice-Hall  (1980)</TD></TR></table>

Revision as of 14:53, 7 June 2020

for a linear stationary control system (an automatic control system)

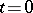The Laplace transform of the response to a unit pulse function (delta-function) with zero conditions at (this response is called the weighting function, the pulse transfer function or the pulse characteristic). An equivalent definition is that the transfer function is the ratio of the Laplace transforms (see Operational calculus) for the output and input signals with zero initial data. The transfer function is a rational-fractional function of the complex variable ; it is the coefficient in the linear relation

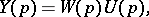(1)

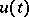relating the Laplace transform of the input of the system (the action, the control) and the Laplace transform of the output (response, reaction) with zero initial conditions. In control theory, relation (1) is represented graphically as:

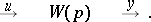For example, let the control system be described by a linear ordinary differential equation with constant coefficients:

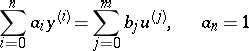(2)

(in an actual system, 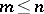usually). Then

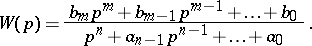(3)

The same expression can be obtained if one uses the operator form of (2) and the differentiation operator ,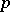

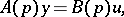to define the transfer function as the ratio of the input operator 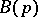to the eigenoperator 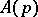; the transfer function (3) of (2) has the following interpretation: If one selects the control , where is a complex number such that 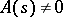, then the linear inhomogeneous equation (2) has the particular solution .

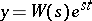The transfer function should not be confused with the step response, which is the response of the system to the unit step function:

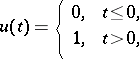with zero initial conditions.

The transfer function is one of the basic concepts in the theory of linear stationary control systems. It is independent of the control actions imposed on the system and is governed only by the parameters of the system itself, thus providing a dynamical characteristic itself. The function 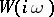of a pure-imaginary argument plays a particular part in control theory; it is called the amplitude-phase, or frequency, characteristic. The concept of a transfer function has been extended also to linear control systems of other types (matrix, non-stationary, discrete, with distributed parameters, etc.).

References

[1] Ya.N. Roitenberg, "Automatic control" , Moscow (1978) (In Russian)
[2] , Mathematical foundations of automatic control theory , Moscow (1971) (In Russian)
[3] R.E. Kalman, P.L. Falb, M.A. Arbib, "Topics in mathematical systems theory" , McGraw-Hill (1969)
[4] A.G. Butkovskii, "Characteristics of systems with distributed parameters: a handbook" , Moscow (1979) (In Russian)


Comments

References

[a1] H. Kwakernaak, R. Sivan, "Linear optimal control systems" , Wiley (Interscience) (1972)
[a2] T. Kailath, "Linear systems" , Prentice-Hall (1980)
How to Cite This Entry:
Transfer function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Transfer_function&oldid=49008
This article was adapted from an original article by N.Kh. Rozov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article
Retrieved from "https://encyclopediaofmath.org/index.php?title=Transfer_function&oldid=49475"