Namespaces
Variants
Actions

Difference between revisions of "Subdifferential"

From Encyclopedia of Mathematics
Jump to: navigation, search
m (tex encoded by computer)
m (Undo revision 48890 by Ulf Rehmann (talk))
Tag: Undo
Line 1: Line 1:
−
<!--
+
''of a convex function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090820/s0908201.png" /> at a point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090820/s0908202.png" />, defined on a space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090820/s0908203.png" /> that is in duality with a space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090820/s0908204.png" />''
−
s0908201.png
 
−
$#A+1 = 31 n = 0
 
−
$#C+1 = 31 : ~/encyclopedia/old_files/data/S090/S.0900820 Subdifferential
 
−
Automatically converted into TeX, above some diagnostics.
 
−
Please remove this comment and the {{TEX|auto}} line below,
 
−
if TeX found to be correct.
 
−
-->
 
  
−
{{TEX|auto}}
+
The set in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090820/s0908205.png" /> defined by:
−
{{TEX|done}}
 
  
−
''of a convex function  $  f: X \rightarrow \mathbf R $
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090820/s0908206.png" /></td> </tr></table>
−
at a point  $  x _ {0} $,
 
−
defined on a space  $  X $
 
−
that is in duality with a space  $  Y $''
 
  
−
The set in $  Y $
+
For example, the subdifferential of the norm <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090820/s0908207.png" /> in a normed space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090820/s0908208.png" /> with dual space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090820/s0908209.png" /> takes the form
−
defined by:
 
  
−
$$
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090820/s09082010.png" /></td> </tr></table>
−
\partial  f( x _ {0} )  = \{ {y \in Y } : {f( x) - f( x _ {0} ) \geq  \langle  y, x- x _ {0} \rangle \ \
 
−
\textrm{ for }  \textrm{ all }  x \in X } \}
 
−
.
 
−
$$
 
  
−
For example, the subdifferential of the norm  $  f( x) = \| x \| $
+
The subdifferential of a convex function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090820/s09082011.png" /> at a point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090820/s09082012.png" /> is a convex set. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090820/s09082013.png" /> is continuous at this point, then the subdifferential is non-empty and compact in the topology <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090820/s09082014.png" />.
−
in a normed space  $  X $
 
−
with dual space  $  X  ^  \star  $
 
−
takes the form
 
  
−
$$
+
The role of the subdifferential of a convex function is similar to that of the derivative in classical analysis. Theorems for subdifferentials that are analogous to theorems for derivatives are valid. For example, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090820/s09082015.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090820/s09082016.png" /> are convex functions and if, at a point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090820/s09082017.png" />, at least one of the functions is continuous, then
−
\partial  f( x)  = \left \{
 
  
−
The subdifferential of a convex function  $  f $
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090820/s09082018.png" /></td> </tr></table>
−
at a point  $  x _ {0} $
 
−
is a convex set. If  $  f $
 
−
is continuous at this point, then the subdifferential is non-empty and compact in the topology  $  \sigma ( Y, X) $.
 
  
−
The role of the subdifferential of a convex function is similar to that of the derivative in classical analysis. Theorems for subdifferentials that are analogous to theorems for derivatives are valid. For example, if  $  f _ {1} $
+
for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090820/s09082019.png" /> (the Moreau–Rockafellar theorem).
−
and  $  f _ {2} $
 
−
are convex functions and if, at a point  $  \overline{x}\; \in ( \mathop{\rm Dom}  f _ {1} ) \cap (  \mathop{\rm Dom}  f _ {2} ) $,
 
−
at least one of the functions is continuous, then
 
  
−
$$
+
At the origin, the subdifferential of the support function of a convex set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090820/s09082020.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090820/s09082021.png" /> that is compact in the topology <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090820/s09082022.png" /> coincides with the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090820/s09082023.png" /> itself. This expresses the duality between convex compact sets and convex closed homogeneous functions (see also [[Support function|Support function]]; [[Supergraph|Supergraph]]; [[Convex analysis|Convex analysis]]).
−
\partial  f _ {1} ( x) + \partial  f _ {2} ( x)  = \partial  ( f _ {1} + f _ {2} )( x)
 
−
$$
 
  
−
for all $ x $(
+
====References====
−
the Moreau–Rockafellar theorem).
+
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> R.T. Rockafellar,  "Convex analysis" , Princeton Univ. Press (1970) {{MR|0274683}} {{ZBL|0193.18401}} </TD></TR></table>
  
−
At the origin, the subdifferential of the support function of a convex set  $  A $
 
−
in  $  X $
 
−
that is compact in the topology  $  \sigma ( Y, X) $
 
−
coincides with the set  $  A $
 
−
itself. This expresses the duality between convex compact sets and convex closed homogeneous functions (see also [[Support function|Support function]]; [[Supergraph|Supergraph]]; [[Convex analysis|Convex analysis]]).
 
  
−
====References====
 
−
<table><TR><TD valign="top">[1]</TD> <TD valign="top">  R.T. Rockafellar,  "Convex analysis" , Princeton Univ. Press  (1970)  {{MR|0274683}} {{ZBL|0193.18401}} </TD></TR></table>
 
  
 
====Comments====
 
====Comments====
−
The $  \sigma ( X, Y) $-
+
The <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090820/s09082025.png" />-topology is the [[Weak topology|weak topology]] on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090820/s09082026.png" /> defined by the family of semi-norms <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090820/s09082027.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090820/s09082028.png" />; this is the weakest topology which makes all the functionals <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090820/s09082029.png" /> continuous.
−
topology is the [[Weak topology|weak topology]] on $  X $
 
−
defined by the family of semi-norms $  p _ {y} ( x) = | \langle  x, y \rangle | $,
 
−
$  y \in Y $;  
 
−
this is the weakest topology which makes all the functionals $  x \rightarrow \langle  x, y \rangle $
 
−
continuous.
 
  
−
The elements $  x  ^  \star  \in \partial  f( x) $
+
The elements <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090820/s09082030.png" /> are called subgradients of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090820/s09082031.png" /> at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090820/s09082032.png" />.
−
are called subgradients of $  f $
 
−
at $  x $.
 
  
 
====References====
 
====References====
 
<table><TR><TD valign="top">[a1]</TD> <TD valign="top">  R. Schneider,  "Boundary structure and curvature of convex bodies"  J. Tölke (ed.)  J.M. Wills (ed.) , ''Contributions to geometry'' , Birkhäuser  (1979)  pp. 13–59  {{MR|0568493}} {{ZBL|0427.52003}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top">  V. Barbu,  Th. Precupanu,  "Convexity and optimization in Banach spaces" , Reidel  (1986)  pp. 101ff  {{MR|0860772}} {{ZBL|0594.49001}} </TD></TR></table>
 
<table><TR><TD valign="top">[a1]</TD> <TD valign="top">  R. Schneider,  "Boundary structure and curvature of convex bodies"  J. Tölke (ed.)  J.M. Wills (ed.) , ''Contributions to geometry'' , Birkhäuser  (1979)  pp. 13–59  {{MR|0568493}} {{ZBL|0427.52003}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top">  V. Barbu,  Th. Precupanu,  "Convexity and optimization in Banach spaces" , Reidel  (1986)  pp. 101ff  {{MR|0860772}} {{ZBL|0594.49001}} </TD></TR></table>

Revision as of 14:53, 7 June 2020

of a convex function 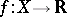at a point 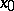, defined on a space 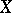that is in duality with a space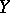

The set in 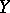defined by:

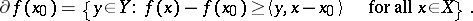For example, the subdifferential of the norm 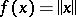in a normed space 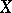with dual space 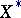takes the form

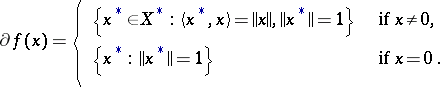The subdifferential of a convex function 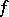at a point 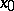is a convex set. If 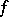is continuous at this point, then the subdifferential is non-empty and compact in the topology .

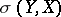The role of the subdifferential of a convex function is similar to that of the derivative in classical analysis. Theorems for subdifferentials that are analogous to theorems for derivatives are valid. For example, if 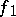and 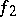are convex functions and if, at a point 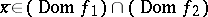, at least one of the functions is continuous, then

for all (the Moreau–Rockafellar theorem).

At the origin, the subdifferential of the support function of a convex set 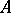in 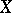that is compact in the topology 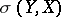coincides with the set itself. This expresses the duality between convex compact sets and convex closed homogeneous functions (see also Support function; Supergraph; Convex analysis).

References

[1] R.T. Rockafellar, "Convex analysis" , Princeton Univ. Press (1970) MR0274683 Zbl 0193.18401


Comments

The 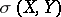-topology is the weak topology on defined by the family of semi-norms 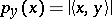, 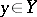; this is the weakest topology which makes all the functionals 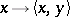continuous.

The elements 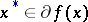are called subgradients of 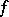at .

References

[a1] R. Schneider, "Boundary structure and curvature of convex bodies" J. Tölke (ed.) J.M. Wills (ed.) , Contributions to geometry , Birkhäuser (1979) pp. 13–59 MR0568493 Zbl 0427.52003
[a2] V. Barbu, Th. Precupanu, "Convexity and optimization in Banach spaces" , Reidel (1986) pp. 101ff MR0860772 Zbl 0594.49001
How to Cite This Entry:
Subdifferential. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Subdifferential&oldid=48890
This article was adapted from an original article by V.M. Tikhomirov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article
Retrieved from "https://encyclopediaofmath.org/index.php?title=Subdifferential&oldid=49456"