Namespaces
Variants
Actions

Difference between revisions of "Stratified sample"

From Encyclopedia of Mathematics
Jump to: navigation, search
m (tex encoded by computer)
m (Undo revision 48869 by Ulf Rehmann (talk))
Tag: Undo
Line 1: Line 1:
−
<!--
+
A [[Sample|sample]] which is broken up into several samples of smaller sizes by certain distinguishing marks (characteristics). Let each element of some sample of size <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090440/s0904401.png" /> possess one and only one of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090440/s0904402.png" /> possible marks. Then the original sample can be broken into <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090440/s0904403.png" /> samples of sizes <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090440/s0904404.png" />, respectively <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090440/s0904405.png" />:
−
s0904401.png
 
−
$#A+1 = 17 n = 0
 
−
$#C+1 = 17 : ~/encyclopedia/old_files/data/S090/S.0900440 Stratified sample
 
−
Automatically converted into TeX, above some diagnostics.
 
−
Please remove this comment and the {{TEX|auto}} line below,
 
−
if TeX found to be correct.
 
−
-->
 
  
−
{{TEX|auto}}
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090440/s0904406.png" /></td> </tr></table>
−
{{TEX|done}}
 
  
−
A [[Sample|sample]] which is broken up into several samples of smaller sizes by certain distinguishing marks (characteristics). Let each element of some sample of size  $  N \geq  2 $
+
where the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090440/s0904407.png" />-th sample <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090440/s0904408.png" /> contains only those elements of the original sample which have the mark <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090440/s0904409.png" />. As a result of this decomposition, the original sample becomes stratified into <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090440/s09044010.png" /> strata <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090440/s09044011.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090440/s09044012.png" />, where the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090440/s09044013.png" />-th stratum contains information about the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090440/s09044014.png" />-th mark. This notion gives rise, for example, to realizations of the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090440/s09044015.png" />-component of a two-dimensional random variable <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090440/s09044016.png" /> whose second component <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090440/s09044017.png" /> has a discrete distribution.
−
possess one and only one of  $  k \geq  2 $
 
−
possible marks. Then the original sample can be broken into $  k $
 
−
samples of sizes  $  n _ {1} \dots n _ {k} $,
 
−
respectively  $  ( n _ {1} + \dots + n _ {k} = N) $:
 
  
−
$$
+
====References====
 +
<table><TR><TD valign="top">[1]</TD> <TD valign="top">  S.S. Wilks,  "Mathematical statistics" , Wiley  (1962)</TD></TR></table>
  
−
where the  $  i $-
 
−
th sample  $  X _ {i1} \dots X _ {in _ {i}  } $
 
−
contains only those elements of the original sample which have the mark  $  i $.
 
−
As a result of this decomposition, the original sample becomes stratified into  $  k $
 
−
strata  $  X _ {i1} \dots X _ {in _ {i}  } $,
 
−
$  i = 1 \dots k $,
 
−
where the  $  i $-
 
−
th stratum contains information about the  $  i $-
 
−
th mark. This notion gives rise, for example, to realizations of the  $  X $-
 
−
component of a two-dimensional random variable  $  ( X, Y) $
 
−
whose second component  $  Y $
 
−
has a discrete distribution.
 
  
−
====References====
 
−
<table><TR><TD valign="top">[1]</TD> <TD valign="top">  S.S. Wilks,  "Mathematical statistics" , Wiley  (1962)</TD></TR></table>
 
  
 
====Comments====
 
====Comments====
 +
  
 
====References====
 
====References====
 
<table><TR><TD valign="top">[a1]</TD> <TD valign="top">  W.G. Cochran,  "Sampling techniques" , Wiley  (1977)</TD></TR></table>
 
<table><TR><TD valign="top">[a1]</TD> <TD valign="top">  W.G. Cochran,  "Sampling techniques" , Wiley  (1977)</TD></TR></table>

Revision as of 14:53, 7 June 2020

A sample which is broken up into several samples of smaller sizes by certain distinguishing marks (characteristics). Let each element of some sample of size possess one and only one of 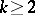possible marks. Then the original sample can be broken into 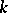samples of sizes , respectively :

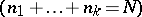where the 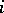-th sample contains only those elements of the original sample which have the mark 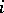. As a result of this decomposition, the original sample becomes stratified into strata , , 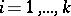where the 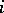-th stratum contains information about the 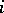-th mark. This notion gives rise, for example, to realizations of the 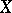-component of a two-dimensional random variable 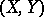whose second component 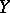has a discrete distribution.

References

[1] S.S. Wilks, "Mathematical statistics" , Wiley (1962)


Comments

References

[a1] W.G. Cochran, "Sampling techniques" , Wiley (1977)
How to Cite This Entry:
Stratified sample. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Stratified_sample&oldid=48869
This article was adapted from an original article by M.S. Nikulin (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article
Retrieved from "https://encyclopediaofmath.org/index.php?title=Stratified_sample&oldid=49450"