Namespaces
Variants
Actions

Difference between revisions of "Stieltjes transform"

From Encyclopedia of Mathematics
Jump to: navigation, search
m (tex encoded by computer)
m (Undo revision 48841 by Ulf Rehmann (talk))
Tag: Undo
Line 1: Line 1:
−
<!--
 
−
s0878101.png
 
−
$#A+1 = 9 n = 0
 
−
$#C+1 = 9 : ~/encyclopedia/old_files/data/S087/S.0807810 Stieltjes transform
 
−
Automatically converted into TeX, above some diagnostics.
 
−
Please remove this comment and the {{TEX|auto}} line below,
 
−
if TeX found to be correct.
 
−
-->
 
−
 
−
{{TEX|auto}}
 
−
{{TEX|done}}
 
−
 
 
The [[Integral transform|integral transform]]
 
The [[Integral transform|integral transform]]
  
−
$$ \tag{* }
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087810/s0878101.png" /></td> <td valign="top" style="width:5%;text-align:right;">(*)</td></tr></table>
−
F( x)  = \int\limits _ { 0 } ^  \infty  f(  
 
−
\frac{x)}{x+}
 
−
t  dt.
 
−
$$
 
  
 
The Stieltjes transform arises in the iteration of the [[Laplace transform|Laplace transform]] and is also a particular case of a convolution transform.
 
The Stieltjes transform arises in the iteration of the [[Laplace transform|Laplace transform]] and is also a particular case of a convolution transform.
  
−
One of the inversion formulas is as follows: If the function $  f( t) \sqrt t $
+
One of the inversion formulas is as follows: If the function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087810/s0878102.png" /> is continuous and bounded on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087810/s0878103.png" />, then
−
is continuous and bounded on $  ( 0, \infty ) $,
 
−
then
 
  
−
$$
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087810/s0878104.png" /></td> </tr></table>
−
\lim\limits _ {n \rightarrow \infty } 
 
−
\frac{(- 1)  ^ {n} }{2 \pi }
 
−
\left (
 
−
\frac{e}{n}
 
−
\right )  ^ {2n} [ x
 
−
^ {2n} F ^ { ( n) } ( x)]  ^ {(} n)  = f( x)
 
−
$$
 
  
−
for $  x \in ( 0, \infty ) $.
+
for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087810/s0878105.png" />.
  
 
The generalized Stieltjes transform is
 
The generalized Stieltjes transform is
  
−
$$
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087810/s0878106.png" /></td> </tr></table>
−
F( x)  = \int\limits _ { 0 } ^  \infty  f( t)
 
−
\frac{dt}{( x+ t)  ^  \rho  }
 
−
,
 
−
$$
 
  
−
where $  \rho $
+
where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087810/s0878107.png" /> is a complex number.
−
is a complex number.
 
  
 
The integrated Stieltjes transform is
 
The integrated Stieltjes transform is
  
−
$$
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087810/s0878108.png" /></td> </tr></table>
−
F( x)  = \int\limits _ { 0 } ^  \infty  K( x, t) f( t)  dt,
 
−
$$
 
  
 
where
 
where
  
−
$$
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087810/s0878109.png" /></td> </tr></table>
−
K( x, t)  = \left \{
 
  
 
Stieltjes transforms are also introduced for generalized functions. The transform (*) was studied by Th.J. Stieltjes (1894–1895).
 
Stieltjes transforms are also introduced for generalized functions. The transform (*) was studied by Th.J. Stieltjes (1894–1895).

Revision as of 14:53, 7 June 2020

The integral transform

(*)

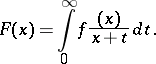The Stieltjes transform arises in the iteration of the Laplace transform and is also a particular case of a convolution transform.

One of the inversion formulas is as follows: If the function 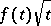is continuous and bounded on 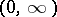, then

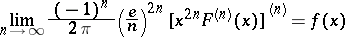for .

The generalized Stieltjes transform is

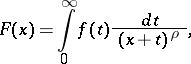where is a complex number.

The integrated Stieltjes transform is

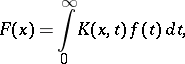where

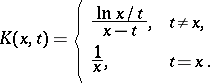Stieltjes transforms are also introduced for generalized functions. The transform (*) was studied by Th.J. Stieltjes (1894–1895).

References

[1] D.V. Widder, "The Laplace transform" , Princeton Univ. Press (1972)
[2] R.P. Boas, D.V. Widder, "The iterated Stieltjes transform" Trans. Amer. Math. Soc. , 45 (1939) pp. 1–72
[3] E.C. Titchmarsh, "Introduction to the theory of Fourier integrals" , Oxford Univ. Press (1948)
[4] Y.A. Brychkov, A.P. Prudnikov, "Integral transforms of generalized functions" , Gordon & Breach (1989) (Translated from Russian)
How to Cite This Entry:
Stieltjes transform. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Stieltjes_transform&oldid=48841
This article was adapted from an original article by Yu.A. BrychkovA.P. Prudnikov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article
Retrieved from "https://encyclopediaofmath.org/index.php?title=Stieltjes_transform&oldid=49447"