Difference between revisions of "Stability criterion"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
Ulf Rehmann (talk | contribs) m (Undo revision 48789 by Ulf Rehmann (talk)) Tag: Undo |
||
| Line 1: | Line 1: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
A necessary and sufficient condition for the real parts of all roots of an equation | A necessary and sufficient condition for the real parts of all roots of an equation | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086950/s0869501.png" /></td> <td valign="top" style="width:5%;text-align:right;">(*)</td></tr></table> | |
| − | |||
| − | |||
to be negative. | to be negative. | ||
| − | A stability criterion is used in applying Lyapunov's theorem on the stability of the first approximation to a fixed point of an autonomous system of differential equations (cf. [[Lyapunov stability|Lyapunov stability]]). The most commonly used stability criterion is the Routh–Hurwitz criterion or Hurwitz criterion: For the real parts of all roots of the equation (*) to be negative it is necessary and sufficient that the inequalities | + | A stability criterion is used in applying Lyapunov's theorem on the stability of the first approximation to a fixed point of an autonomous system of differential equations (cf. [[Lyapunov stability|Lyapunov stability]]). The most commonly used stability criterion is the Routh–Hurwitz criterion or Hurwitz criterion: For the real parts of all roots of the equation (*) to be negative it is necessary and sufficient that the inequalities <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086950/s0869502.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086950/s0869503.png" />, be satisfied, where |
| − | |||
| − | be satisfied, where | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086950/s0869504.png" /></td> </tr></table> | |
| − | |||
| − | |||
are the principal diagonal minors of the matrix | are the principal diagonal minors of the matrix | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086950/s0869505.png" /></td> </tr></table> | |
| − | |||
| − | (on the main diagonal of this matrix there stand | + | (on the main diagonal of this matrix there stand <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086950/s0869506.png" />; for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086950/s0869507.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086950/s0869508.png" />). |
| − | for | ||
| − | |||
| − | For | + | For <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086950/s0869509.png" /> the Routh–Hurwitz stability criterion takes a particularly simple form: For the real parts of the roots of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086950/s08695010.png" /> to be negative it is necessary and sufficient that the coefficients of the equation be positive: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086950/s08695011.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086950/s08695012.png" />. |
| − | the Routh–Hurwitz stability criterion takes a particularly simple form: For the real parts of the roots of | ||
| − | to be negative it is necessary and sufficient that the coefficients of the equation be positive: | ||
| − | |||
| − | For each | + | For each <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086950/s08695013.png" />, for the real parts of all roots of the equation (*) to be negative it is necessary (but for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086950/s08695014.png" /> not sufficient) that all coefficients of the equation be positive: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086950/s08695015.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086950/s08695016.png" />. If at least one of the determinants <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086950/s08695017.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086950/s08695018.png" />, is negative, then there is a root of (*) with positive real part (this assertion is used in applying Lyapunov's theorem on the instability of the first approximation to a fixed point of an autonomous system of differential equations, cf. [[Lyapunov stability|Lyapunov stability]]). If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086950/s08695019.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086950/s08695020.png" />, but <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086950/s08695021.png" /> for a certain <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086950/s08695022.png" />, then the location of the roots of the equation (*) relative to the imaginary axis can also be described without finding the roots (cf. [[#References|[5]]], [[#References|[8]]], Chapt. XVI, Sect. 8). |
| − | for the real parts of all roots of the equation (*) to be negative it is necessary (but for | ||
| − | not sufficient) that all coefficients of the equation be positive: | ||
| − | |||
| − | If at least one of the determinants | ||
| − | |||
| − | is negative, then there is a root of (*) with positive real part (this assertion is used in applying Lyapunov's theorem on the instability of the first approximation to a fixed point of an autonomous system of differential equations, cf. [[Lyapunov stability|Lyapunov stability]]). If | ||
| − | for all | ||
| − | but | ||
| − | for a certain | ||
| − | then the location of the roots of the equation (*) relative to the imaginary axis can also be described without finding the roots (cf. [[#References|[5]]], [[#References|[8]]], Chapt. XVI, Sect. 8). | ||
| − | Much simpler in applications is the Liénard–Chipart criterion: For the real parts of all roots of the equation (*) to be negative it is necessary and sufficient that the following inequalities hold: | + | Much simpler in applications is the Liénard–Chipart criterion: For the real parts of all roots of the equation (*) to be negative it is necessary and sufficient that the following inequalities hold: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086950/s08695023.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086950/s08695024.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086950/s08695025.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086950/s08695026.png" /> (the determinant <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086950/s08695027.png" /> is the same as in the Routh–Hurwitz criterion). |
| − | |||
| − | |||
| − | |||
| − | the determinant | ||
| − | is the same as in the Routh–Hurwitz criterion). | ||
Hermite's criterion (historically the first, cf. [[#References|[1]]], [[#References|[10]]], Sect. 3.1) allows one to determine with the help of a finite number of arithmetic operations on the coefficients of (*) whether all roots of this equation have negative real parts. The Routh–Hurwitz criterion formulated above is a modification of Hermite's criterion found by A. Hurwitz. A Lyapunov stability criterion is also known (cf. [[#References|[3]]], [[#References|[8]]], Chapt. XVI, Sect. 5, [[#References|[10]]], Sect. 3.5). | Hermite's criterion (historically the first, cf. [[#References|[1]]], [[#References|[10]]], Sect. 3.1) allows one to determine with the help of a finite number of arithmetic operations on the coefficients of (*) whether all roots of this equation have negative real parts. The Routh–Hurwitz criterion formulated above is a modification of Hermite's criterion found by A. Hurwitz. A Lyapunov stability criterion is also known (cf. [[#References|[3]]], [[#References|[8]]], Chapt. XVI, Sect. 5, [[#References|[10]]], Sect. 3.5). | ||
| − | For a study of the stability of fixed points of differentiable mappings (autonomous systems with discrete time) as well as for a study of [[Orbit stability|orbit stability]] of closed trajectories of autonomous systems of differential equations one has to apply necessary and sufficient conditions for the absolute values of all roots of the equation (*) to be less than one. This criterion is obtained from the above-mentioned stability criterion by the mapping | + | For a study of the stability of fixed points of differentiable mappings (autonomous systems with discrete time) as well as for a study of [[Orbit stability|orbit stability]] of closed trajectories of autonomous systems of differential equations one has to apply necessary and sufficient conditions for the absolute values of all roots of the equation (*) to be less than one. This criterion is obtained from the above-mentioned stability criterion by the mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086950/s08695028.png" /> from the open unit disc onto the open left half-plane (cf. [[#References|[10]]], Sect. 3.2). |
| − | from the open unit disc onto the open left half-plane (cf. [[#References|[10]]], Sect. 3.2). | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> C. Hermite, "Sur le nombre des racines d'une équation algébrique comprise entre des limites donnés" ''J. Reine Angew. Math.'' , '''52''' (1856) pp. 39–51</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> E.J. Routh, "A treatise on the stability of a given state of motion" , Macmillan (1877)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> A.M. Lyapunov, "Stability of motion" , Acad. Press (1966) (Translated from Russian)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> A. Hurwitz, "Ueber die Bedingungen, unter welchen eine Gleichung nur Wurzeln mit negativen reellen Theilen besitzt" ''Math. Ann.'' , '''46''' (1895) pp. 273–284</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> L. Orlando, "Sul problema di Hurwitz relative alle parti reali delle radici di un'equazione algebrica" ''Math. Ann.'' , '''71''' (1911) pp. 233–245</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> A. Liénard, M.H. Chipart, "Sur le signe de la partie réelle des racines d'une équation algébrique" ''J. Math. Pure Appl. (6)'' , '''10''' (1914) pp. 291–346</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> N.G. Chetaev, "Stability of motion" , Moscow (1965) (In Russian)</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> F.R. [F.R. Gantmakher] Gantmacher, "The theory of matrices" , '''1''' , Chelsea, reprint (1977) (Translated from Russian)</TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> B.P. Demidovich, "Lectures on the mathematical theory of stability" , Moscow (1967) (In Russian)</TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> E. Jury, "Inners and stability of dynamic systems" , Wiley (1974)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> C. Hermite, "Sur le nombre des racines d'une équation algébrique comprise entre des limites donnés" ''J. Reine Angew. Math.'' , '''52''' (1856) pp. 39–51</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> E.J. Routh, "A treatise on the stability of a given state of motion" , Macmillan (1877)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> A.M. Lyapunov, "Stability of motion" , Acad. Press (1966) (Translated from Russian)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> A. Hurwitz, "Ueber die Bedingungen, unter welchen eine Gleichung nur Wurzeln mit negativen reellen Theilen besitzt" ''Math. Ann.'' , '''46''' (1895) pp. 273–284</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> L. Orlando, "Sul problema di Hurwitz relative alle parti reali delle radici di un'equazione algebrica" ''Math. Ann.'' , '''71''' (1911) pp. 233–245</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> A. Liénard, M.H. Chipart, "Sur le signe de la partie réelle des racines d'une équation algébrique" ''J. Math. Pure Appl. (6)'' , '''10''' (1914) pp. 291–346</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> N.G. Chetaev, "Stability of motion" , Moscow (1965) (In Russian)</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> F.R. [F.R. Gantmakher] Gantmacher, "The theory of matrices" , '''1''' , Chelsea, reprint (1977) (Translated from Russian)</TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> B.P. Demidovich, "Lectures on the mathematical theory of stability" , Moscow (1967) (In Russian)</TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> E. Jury, "Inners and stability of dynamic systems" , Wiley (1974)</TD></TR></table> | ||
| + | |||
| + | |||
====Comments==== | ====Comments==== | ||
| − | See also [[Mikhailov criterion|Mikhailov criterion]], which is equivalent to the Routh–Hurwitz criterion, but formulated in terms of the curve obtained from (*) by letting | + | See also [[Mikhailov criterion|Mikhailov criterion]], which is equivalent to the Routh–Hurwitz criterion, but formulated in terms of the curve obtained from (*) by letting <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086950/s08695029.png" /> vary over the positive imaginary axis. |
| − | vary over the positive imaginary axis. | ||
In control theory (robust control) one is often concerned with the stability of a whole family of polynomials rather than a single one. Stability results pertaining to this situation are generally known as Kharitonov-type theorems. | In control theory (robust control) one is often concerned with the stability of a whole family of polynomials rather than a single one. Stability results pertaining to this situation are generally known as Kharitonov-type theorems. | ||
| − | The original Kharitonov theorem, [[#References|[a1]]], [[#References|[a2]]], can be stated as follows. Let | + | The original Kharitonov theorem, [[#References|[a1]]], [[#References|[a2]]], can be stated as follows. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086950/s08695030.png" /> be the family of polynomials |
| − | be the family of polynomials | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086950/s08695031.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | where each | + | where each <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086950/s08695032.png" /> ranges over a given closed interval <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086950/s08695033.png" />. Form the four polynomials |
| − | ranges over a given closed interval | ||
| − | Form the four polynomials | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086950/s08695034.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086950/s08695035.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086950/s08695036.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086950/s08695037.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086950/s08695038.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086950/s08695039.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086950/s08695040.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086950/s08695041.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | Then every polynomial | + | Then every polynomial <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086950/s08695042.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086950/s08695043.png" />, has its zeros strictly in the left half-plane if and only if the four polynomials <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086950/s08695044.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086950/s08695045.png" />, have this property. |
| − | |||
| − | has its zeros strictly in the left half-plane if and only if the four polynomials | ||
| − | |||
| − | have this property. | ||
There is a large variety of similar theorems applying to other regions of allowed zeros, otherwise shaped families of polynomials (than cubes such as above), and discrete-time stability. Cf. [[#References|[a3]]] for a survey. | There is a large variety of similar theorems applying to other regions of allowed zeros, otherwise shaped families of polynomials (than cubes such as above), and discrete-time stability. Cf. [[#References|[a3]]] for a survey. | ||
Revision as of 14:53, 7 June 2020
A necessary and sufficient condition for the real parts of all roots of an equation
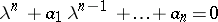 | (*) |
to be negative.
A stability criterion is used in applying Lyapunov's theorem on the stability of the first approximation to a fixed point of an autonomous system of differential equations (cf. Lyapunov stability). The most commonly used stability criterion is the Routh–Hurwitz criterion or Hurwitz criterion: For the real parts of all roots of the equation (*) to be negative it is necessary and sufficient that the inequalities 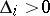 ,
, 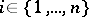 , be satisfied, where
, be satisfied, where
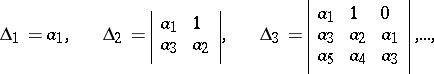 |
are the principal diagonal minors of the matrix
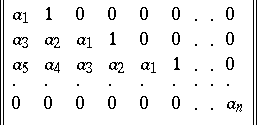 |
(on the main diagonal of this matrix there stand  ; for
; for 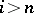 ,
, 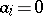 ).
).
For 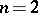 the Routh–Hurwitz stability criterion takes a particularly simple form: For the real parts of the roots of
the Routh–Hurwitz stability criterion takes a particularly simple form: For the real parts of the roots of 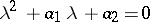 to be negative it is necessary and sufficient that the coefficients of the equation be positive:
to be negative it is necessary and sufficient that the coefficients of the equation be positive: 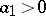 ,
,  .
.
For each  , for the real parts of all roots of the equation (*) to be negative it is necessary (but for
, for the real parts of all roots of the equation (*) to be negative it is necessary (but for 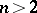 not sufficient) that all coefficients of the equation be positive:
not sufficient) that all coefficients of the equation be positive: 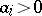 ,
, 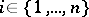 . If at least one of the determinants
. If at least one of the determinants 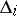 ,
, 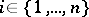 , is negative, then there is a root of (*) with positive real part (this assertion is used in applying Lyapunov's theorem on the instability of the first approximation to a fixed point of an autonomous system of differential equations, cf. Lyapunov stability). If
, is negative, then there is a root of (*) with positive real part (this assertion is used in applying Lyapunov's theorem on the instability of the first approximation to a fixed point of an autonomous system of differential equations, cf. Lyapunov stability). If 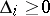 for all
for all  , but
, but 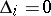 for a certain
for a certain 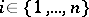 , then the location of the roots of the equation (*) relative to the imaginary axis can also be described without finding the roots (cf. [5], [8], Chapt. XVI, Sect. 8).
, then the location of the roots of the equation (*) relative to the imaginary axis can also be described without finding the roots (cf. [5], [8], Chapt. XVI, Sect. 8).
Much simpler in applications is the Liénard–Chipart criterion: For the real parts of all roots of the equation (*) to be negative it is necessary and sufficient that the following inequalities hold: 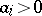 ,
, 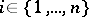 ,
, 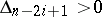 ,
, 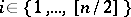 (the determinant
(the determinant 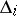 is the same as in the Routh–Hurwitz criterion).
is the same as in the Routh–Hurwitz criterion).
Hermite's criterion (historically the first, cf. [1], [10], Sect. 3.1) allows one to determine with the help of a finite number of arithmetic operations on the coefficients of (*) whether all roots of this equation have negative real parts. The Routh–Hurwitz criterion formulated above is a modification of Hermite's criterion found by A. Hurwitz. A Lyapunov stability criterion is also known (cf. [3], [8], Chapt. XVI, Sect. 5, [10], Sect. 3.5).
For a study of the stability of fixed points of differentiable mappings (autonomous systems with discrete time) as well as for a study of orbit stability of closed trajectories of autonomous systems of differential equations one has to apply necessary and sufficient conditions for the absolute values of all roots of the equation (*) to be less than one. This criterion is obtained from the above-mentioned stability criterion by the mapping 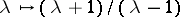 from the open unit disc onto the open left half-plane (cf. [10], Sect. 3.2).
from the open unit disc onto the open left half-plane (cf. [10], Sect. 3.2).
References
| [1] | C. Hermite, "Sur le nombre des racines d'une équation algébrique comprise entre des limites donnés" J. Reine Angew. Math. , 52 (1856) pp. 39–51 |
| [2] | E.J. Routh, "A treatise on the stability of a given state of motion" , Macmillan (1877) |
| [3] | A.M. Lyapunov, "Stability of motion" , Acad. Press (1966) (Translated from Russian) |
| [4] | A. Hurwitz, "Ueber die Bedingungen, unter welchen eine Gleichung nur Wurzeln mit negativen reellen Theilen besitzt" Math. Ann. , 46 (1895) pp. 273–284 |
| [5] | L. Orlando, "Sul problema di Hurwitz relative alle parti reali delle radici di un'equazione algebrica" Math. Ann. , 71 (1911) pp. 233–245 |
| [6] | A. Liénard, M.H. Chipart, "Sur le signe de la partie réelle des racines d'une équation algébrique" J. Math. Pure Appl. (6) , 10 (1914) pp. 291–346 |
| [7] | N.G. Chetaev, "Stability of motion" , Moscow (1965) (In Russian) |
| [8] | F.R. [F.R. Gantmakher] Gantmacher, "The theory of matrices" , 1 , Chelsea, reprint (1977) (Translated from Russian) |
| [9] | B.P. Demidovich, "Lectures on the mathematical theory of stability" , Moscow (1967) (In Russian) |
| [10] | E. Jury, "Inners and stability of dynamic systems" , Wiley (1974) |
Comments
See also Mikhailov criterion, which is equivalent to the Routh–Hurwitz criterion, but formulated in terms of the curve obtained from (*) by letting 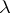 vary over the positive imaginary axis.
vary over the positive imaginary axis.
In control theory (robust control) one is often concerned with the stability of a whole family of polynomials rather than a single one. Stability results pertaining to this situation are generally known as Kharitonov-type theorems.
The original Kharitonov theorem, [a1], [a2], can be stated as follows. Let 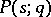 be the family of polynomials
be the family of polynomials
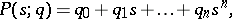 |
where each 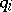 ranges over a given closed interval
ranges over a given closed interval 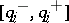 . Form the four polynomials
. Form the four polynomials
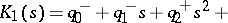 |
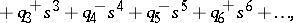 |
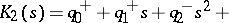 |
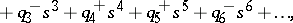 |
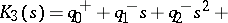 |
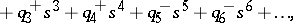 |
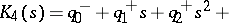 |
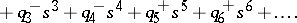 |
Then every polynomial 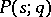 ,
, 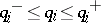 , has its zeros strictly in the left half-plane if and only if the four polynomials
, has its zeros strictly in the left half-plane if and only if the four polynomials 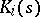 ,
, 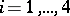 , have this property.
, have this property.
There is a large variety of similar theorems applying to other regions of allowed zeros, otherwise shaped families of polynomials (than cubes such as above), and discrete-time stability. Cf. [a3] for a survey.
References
| [a1] | V.L. Kharitonov, "Asymptotic stability of an equilibrium position of a family of systems of linear differential equations" Diff. Uravn. , 14 : 11 (1978) pp. 1483–1485 (In Russian) |
| [a2] | V.L. Kharitonov, "On a generalization of a stability criterion" Akad. Nauk KazakhsSSR, Fiz.-Mat. , 1 (1978) pp. 53–57 (In Russian) |
| [a3] | B.R. Barmish, B. Ross, "New tools for robustness analysis" , Proc. 27-th IEEE CDC , IEEE (1988) pp. 1–6 |
Stability criterion. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Stability_criterion&oldid=48789