Difference between revisions of "Skew-symmetric bilinear form"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
Ulf Rehmann (talk | contribs) m (Undo revision 48725 by Ulf Rehmann (talk)) Tag: Undo |
||
| Line 1: | Line 1: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
''anti-symmetric bilinear form'' | ''anti-symmetric bilinear form'' | ||
| − | A [[Bilinear form|bilinear form]] | + | A [[Bilinear form|bilinear form]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085710/s0857101.png" /> on a unitary <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085710/s0857102.png" />-module <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085710/s0857103.png" /> (where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085710/s0857104.png" /> is a commutative ring with an identity) such that |
| − | on a unitary | ||
| − | module | ||
| − | where | ||
| − | is a commutative ring with an identity) such that | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085710/s0857105.png" /></td> </tr></table> | |
| − | |||
| − | - | ||
| − | |||
| − | |||
| − | |||
| − | The structure of any skew-symmetric bilinear form | + | The structure of any skew-symmetric bilinear form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085710/s0857106.png" /> on a finite-dimensional vector space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085710/s0857107.png" /> over a field of characteristic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085710/s0857108.png" /> is uniquely determined by its Witt index <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085710/s0857109.png" /> (see [[Witt theorem|Witt theorem]]; [[Witt decomposition|Witt decomposition]]). Namely: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085710/s08571010.png" /> is the orthogonal (with respect to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085710/s08571011.png" />) direct sum of the kernel <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085710/s08571012.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085710/s08571013.png" /> and a subspace of dimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085710/s08571014.png" />, the restriction of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085710/s08571015.png" /> to which is a standard form. Two skew-symmetric bilinear forms on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085710/s08571016.png" /> are isometric if and only if their Witt indices are equal. In particular, a non-degenerate skew-symmetric bilinear form is standard, and in that case the dimension of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085710/s08571017.png" /> is even. |
| − | on a finite-dimensional vector space | ||
| − | over a field of characteristic | ||
| − | is uniquely determined by its Witt index | ||
| − | see [[Witt theorem|Witt theorem]]; [[Witt decomposition|Witt decomposition]]). Namely: | ||
| − | is the orthogonal (with respect to | ||
| − | direct sum of the kernel | ||
| − | of | ||
| − | and a subspace of dimension | ||
| − | the restriction of | ||
| − | to which is a standard form. Two skew-symmetric bilinear forms on | ||
| − | are isometric if and only if their Witt indices are equal. In particular, a non-degenerate skew-symmetric bilinear form is standard, and in that case the dimension of | ||
| − | is even. | ||
| − | For any skew-symmetric bilinear form | + | For any skew-symmetric bilinear form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085710/s08571018.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085710/s08571019.png" /> there exists a basis <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085710/s08571020.png" /> relative to which the matrix of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085710/s08571021.png" /> is of the form |
| − | on | ||
| − | there exists a basis | ||
| − | relative to which the matrix of | ||
| − | is of the form | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085710/s08571022.png" /></td> <td valign="top" style="width:5%;text-align:right;">(*)</td></tr></table> | |
| − | |||
| − | where | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085710/s08571023.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085710/s08571024.png" /> is the identity matrix of order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085710/s08571025.png" />. The matrix of a skew-symmetric bilinear form relative to any basis is skew-symmetric. Therefore, the above properties of skew-symmetric bilinear forms can be formulated as follows: For any skew-symmetric matrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085710/s08571026.png" /> over a field of characteristic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085710/s08571027.png" /> there exists a non-singular matrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085710/s08571028.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085710/s08571029.png" /> is of the form (*). In particular, the rank of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085710/s08571030.png" /> is even, and the determinant of a skew-symmetric matrix of odd order is 0. |
| − | and | ||
| − | is the identity matrix of order | ||
| − | The matrix of a skew-symmetric bilinear form relative to any basis is skew-symmetric. Therefore, the above properties of skew-symmetric bilinear forms can be formulated as follows: For any skew-symmetric matrix | ||
| − | over a field of characteristic | ||
| − | there exists a non-singular matrix | ||
| − | such that | ||
| − | is of the form (*). In particular, the rank of | ||
| − | is even, and the determinant of a skew-symmetric matrix of odd order is 0. | ||
| − | The above assertions remain valid for a field of characteristic 2, provided one replaces the skew-symmetry condition for the form | + | The above assertions remain valid for a field of characteristic 2, provided one replaces the skew-symmetry condition for the form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085710/s08571031.png" /> by the condition that the form be alternating: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085710/s08571032.png" /> for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085710/s08571033.png" /> (for fields of characteristic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085710/s08571034.png" /> the two conditions are equivalent). |
| − | by the condition that the form be alternating: | ||
| − | for any | ||
| − | for fields of characteristic | ||
| − | the two conditions are equivalent). | ||
| − | These results can be generalized to the case where | + | These results can be generalized to the case where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085710/s08571035.png" /> is a commutative principal ideal ring, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085710/s08571036.png" /> is a free <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085710/s08571037.png" />-module of finite dimension and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085710/s08571038.png" /> is an alternating bilinear form on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085710/s08571039.png" />. To be precise: Under these assumptions there exists a basis <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085710/s08571040.png" /> of the module <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085710/s08571041.png" /> and a non-negative integer <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085710/s08571042.png" /> such that |
| − | is a commutative principal ideal ring, | ||
| − | is a free | ||
| − | module of finite dimension and | ||
| − | is an alternating bilinear form on | ||
| − | To be precise: Under these assumptions there exists a basis | ||
| − | of the module | ||
| − | and a non-negative integer | ||
| − | such that | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085710/s08571043.png" /></td> </tr></table> | |
| − | 0 | ||
| − | |||
| − | |||
| − | |||
| − | and | + | and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085710/s08571044.png" /> divides <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085710/s08571045.png" /> for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085710/s08571046.png" />; otherwise <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085710/s08571047.png" />. The ideals <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085710/s08571048.png" /> are uniquely determined by these conditions, and the module <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085710/s08571049.png" /> is generated by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085710/s08571050.png" />. |
| − | divides | ||
| − | for | ||
| − | otherwise | ||
| − | The ideals | ||
| − | are uniquely determined by these conditions, and the module | ||
| − | is generated by | ||
| − | The determinant of an alternating matrix of odd order equals 0 for any commutative ring | + | The determinant of an alternating matrix of odd order equals 0 for any commutative ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085710/s08571051.png" /> with an identity. In case the order of the alternating matrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085710/s08571052.png" /> over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085710/s08571053.png" /> is even, the element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085710/s08571054.png" /> is a square in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085710/s08571055.png" /> (see [[Pfaffian|Pfaffian]]). |
| − | with an identity. In case the order of the alternating matrix | ||
| − | over | ||
| − | is even, the element | ||
| − | is a square in | ||
| − | see [[Pfaffian|Pfaffian]]). | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> N. Bourbaki, "Algèbre" , ''Eléments de mathématiques'' , Hermann (1970) pp. Chapt. II. Algèbre linéaire</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> S. Lang, "Algebra" , Addison-Wesley (1984)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> E. Artin, "Geometric algebra" , Interscience (1957)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> N. Bourbaki, "Algèbre" , ''Eléments de mathématiques'' , Hermann (1970) pp. Chapt. II. Algèbre linéaire</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> S. Lang, "Algebra" , Addison-Wesley (1984)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> E. Artin, "Geometric algebra" , Interscience (1957)</TD></TR></table> | ||
| + | |||
| + | |||
====Comments==== | ====Comments==== | ||
Revision as of 14:53, 7 June 2020
anti-symmetric bilinear form
A bilinear form 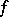 on a unitary
on a unitary 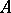 -module
-module  (where
(where 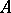 is a commutative ring with an identity) such that
is a commutative ring with an identity) such that
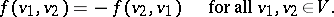 |
The structure of any skew-symmetric bilinear form 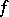 on a finite-dimensional vector space
on a finite-dimensional vector space 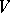 over a field of characteristic
over a field of characteristic 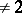 is uniquely determined by its Witt index
is uniquely determined by its Witt index 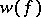 (see Witt theorem; Witt decomposition). Namely:
(see Witt theorem; Witt decomposition). Namely: 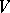 is the orthogonal (with respect to
is the orthogonal (with respect to 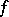 ) direct sum of the kernel
) direct sum of the kernel 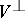 of
of 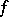 and a subspace of dimension
and a subspace of dimension 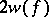 , the restriction of
, the restriction of 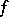 to which is a standard form. Two skew-symmetric bilinear forms on
to which is a standard form. Two skew-symmetric bilinear forms on 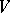 are isometric if and only if their Witt indices are equal. In particular, a non-degenerate skew-symmetric bilinear form is standard, and in that case the dimension of
are isometric if and only if their Witt indices are equal. In particular, a non-degenerate skew-symmetric bilinear form is standard, and in that case the dimension of 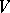 is even.
is even.
For any skew-symmetric bilinear form 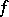 on
on  there exists a basis
there exists a basis  relative to which the matrix of
relative to which the matrix of 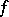 is of the form
is of the form
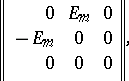 | (*) |
where 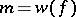 and
and 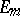 is the identity matrix of order
is the identity matrix of order 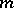 . The matrix of a skew-symmetric bilinear form relative to any basis is skew-symmetric. Therefore, the above properties of skew-symmetric bilinear forms can be formulated as follows: For any skew-symmetric matrix
. The matrix of a skew-symmetric bilinear form relative to any basis is skew-symmetric. Therefore, the above properties of skew-symmetric bilinear forms can be formulated as follows: For any skew-symmetric matrix 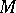 over a field of characteristic
over a field of characteristic 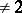 there exists a non-singular matrix
there exists a non-singular matrix 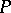 such that
such that 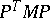 is of the form (*). In particular, the rank of
is of the form (*). In particular, the rank of 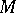 is even, and the determinant of a skew-symmetric matrix of odd order is 0.
is even, and the determinant of a skew-symmetric matrix of odd order is 0.
The above assertions remain valid for a field of characteristic 2, provided one replaces the skew-symmetry condition for the form 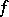 by the condition that the form be alternating:
by the condition that the form be alternating: 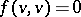 for any
for any 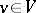 (for fields of characteristic
(for fields of characteristic 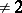 the two conditions are equivalent).
the two conditions are equivalent).
These results can be generalized to the case where 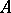 is a commutative principal ideal ring,
is a commutative principal ideal ring, 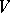 is a free
is a free 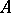 -module of finite dimension and
-module of finite dimension and 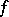 is an alternating bilinear form on
is an alternating bilinear form on 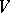 . To be precise: Under these assumptions there exists a basis
. To be precise: Under these assumptions there exists a basis  of the module
of the module 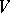 and a non-negative integer
and a non-negative integer 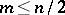 such that
such that
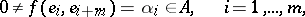 |
and 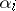 divides
divides 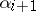 for
for 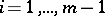 ; otherwise
; otherwise 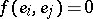 . The ideals
. The ideals 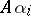 are uniquely determined by these conditions, and the module
are uniquely determined by these conditions, and the module 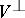 is generated by
is generated by 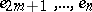 .
.
The determinant of an alternating matrix of odd order equals 0 for any commutative ring 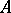 with an identity. In case the order of the alternating matrix
with an identity. In case the order of the alternating matrix 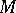 over
over 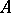 is even, the element
is even, the element 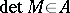 is a square in
is a square in 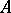 (see Pfaffian).
(see Pfaffian).
References
| [1] | N. Bourbaki, "Algèbre" , Eléments de mathématiques , Hermann (1970) pp. Chapt. II. Algèbre linéaire |
| [2] | S. Lang, "Algebra" , Addison-Wesley (1984) |
| [3] | E. Artin, "Geometric algebra" , Interscience (1957) |
Comments
The kernel of a skew-symmetric bilinear form is the left kernel of the corresponding bilinear mapping, which is equal to the right kernel by skew symmetry.
References
| [a1] | J. Milnor, D. Husemoller, "Symmetric bilinear forms" , Springer (1973) |
Skew-symmetric bilinear form. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Skew-symmetric_bilinear_form&oldid=48725