Difference between revisions of "Sign test"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
Ulf Rehmann (talk | contribs) m (Undo revision 48694 by Ulf Rehmann (talk)) Tag: Undo |
||
| Line 1: | Line 1: | ||
| − | + | A [[Non-parametric test|non-parametric test]] for a hypothesis <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085040/s0850401.png" />, according to which a random variable <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085040/s0850402.png" /> has a binomial distribution with parameters <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085040/s0850403.png" />. If the hypothesis <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085040/s0850404.png" /> is true, then | |
| − | s0850401.png | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085040/s0850405.png" /></td> </tr></table> | |
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085040/s0850406.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
where | where | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085040/s0850407.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | 0 | ||
| − | |||
| − | and | + | and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085040/s0850408.png" /> is the beta-function. According to the sign test with significance level <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085040/s0850409.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085040/s08504010.png" />, the hypothesis <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085040/s08504011.png" /> is rejected if |
| − | is the beta-function. According to the sign test with significance level | ||
| − | |||
| − | the hypothesis | ||
| − | is rejected if | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085040/s08504012.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | where | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085040/s08504013.png" />, the critical value of the test, is the integer solution of the inequalities |
| − | the critical value of the test, is the integer solution of the inequalities | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085040/s08504014.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | The sign test can be used to test a hypothesis | + | The sign test can be used to test a hypothesis <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085040/s08504015.png" /> according to which the unknown continuous distribution of independent identically-distributed random variables <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085040/s08504016.png" /> is symmetric about zero, i.e. for any real <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085040/s08504017.png" />, |
| − | according to which the unknown continuous distribution of independent identically-distributed random variables | ||
| − | is symmetric about zero, i.e. for any real | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085040/s08504018.png" /></td> </tr></table> | |
| − | |||
| − | |||
In this case the sign test is based on the statistic | In this case the sign test is based on the statistic | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085040/s08504019.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | which is governed by a binomial law with parameters | + | which is governed by a binomial law with parameters <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085040/s08504020.png" /> if the hypothesis <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085040/s08504021.png" /> is true. |
| − | if the hypothesis | ||
| − | is true. | ||
| − | Similarly, the sign test is used to test a hypothesis | + | Similarly, the sign test is used to test a hypothesis <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085040/s08504022.png" /> according to which the median of an unknown continuous distribution to which independent random variables <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085040/s08504023.png" /> are subject is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085040/s08504024.png" />; to this end one simply replaces the given random variables by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085040/s08504025.png" />. |
| − | according to which the median of an unknown continuous distribution to which independent random variables | ||
| − | are subject is | ||
| − | to this end one simply replaces the given random variables by | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> L.N. Bol'shev, N.V. Smirnov, "Tables of mathematical statistics" , ''Libr. math. tables'' , '''46''' , Nauka (1983) (In Russian) (Processed by L.S. Bark and E.S. Kedrova)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> E.L. Lehmann, "Testing statistical hypotheses" , Wiley (1986)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> B.L. van der Waerden, "Mathematische Statistik" , Springer (1957)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> N.V. Smirnov, I.V. Dunin-Barkovskii, "Mathematische Statistik in der Technik" , Deutsch. Verlag Wissenschaft. (1969) (Translated from Russian)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> L.N. Bol'shev, N.V. Smirnov, "Tables of mathematical statistics" , ''Libr. math. tables'' , '''46''' , Nauka (1983) (In Russian) (Processed by L.S. Bark and E.S. Kedrova)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> E.L. Lehmann, "Testing statistical hypotheses" , Wiley (1986)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> B.L. van der Waerden, "Mathematische Statistik" , Springer (1957)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> N.V. Smirnov, I.V. Dunin-Barkovskii, "Mathematische Statistik in der Technik" , Deutsch. Verlag Wissenschaft. (1969) (Translated from Russian)</TD></TR></table> | ||
Revision as of 14:53, 7 June 2020
A non-parametric test for a hypothesis 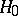 , according to which a random variable
, according to which a random variable 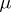 has a binomial distribution with parameters
has a binomial distribution with parameters 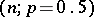 . If the hypothesis
. If the hypothesis 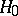 is true, then
is true, then
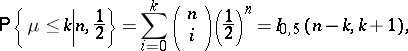 |
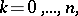 |
where
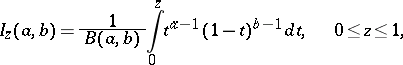 |
and 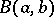 is the beta-function. According to the sign test with significance level
is the beta-function. According to the sign test with significance level 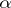 ,
, 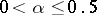 , the hypothesis
, the hypothesis 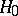 is rejected if
is rejected if
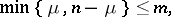 |
where 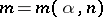 , the critical value of the test, is the integer solution of the inequalities
, the critical value of the test, is the integer solution of the inequalities
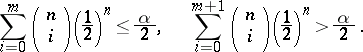 |
The sign test can be used to test a hypothesis 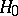 according to which the unknown continuous distribution of independent identically-distributed random variables
according to which the unknown continuous distribution of independent identically-distributed random variables 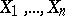 is symmetric about zero, i.e. for any real
is symmetric about zero, i.e. for any real  ,
,
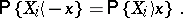 |
In this case the sign test is based on the statistic
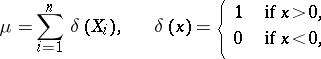 |
which is governed by a binomial law with parameters 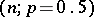 if the hypothesis
if the hypothesis 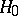 is true.
is true.
Similarly, the sign test is used to test a hypothesis 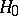 according to which the median of an unknown continuous distribution to which independent random variables
according to which the median of an unknown continuous distribution to which independent random variables 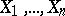 are subject is
are subject is 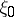 ; to this end one simply replaces the given random variables by
; to this end one simply replaces the given random variables by 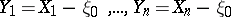 .
.
References
| [1] | L.N. Bol'shev, N.V. Smirnov, "Tables of mathematical statistics" , Libr. math. tables , 46 , Nauka (1983) (In Russian) (Processed by L.S. Bark and E.S. Kedrova) |
| [2] | E.L. Lehmann, "Testing statistical hypotheses" , Wiley (1986) |
| [3] | B.L. van der Waerden, "Mathematische Statistik" , Springer (1957) |
| [4] | N.V. Smirnov, I.V. Dunin-Barkovskii, "Mathematische Statistik in der Technik" , Deutsch. Verlag Wissenschaft. (1969) (Translated from Russian) |
Sign test. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Sign_test&oldid=48694