Difference between revisions of "Schur theorems"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
Ulf Rehmann (talk | contribs) m (Undo revision 48627 by Ulf Rehmann (talk)) Tag: Undo |
||
| Line 1: | Line 1: | ||
| − | < | + | Theorems for finding a solution to the [[Coefficient problem|coefficient problem]] for bounded analytic functions. They were obtained by I. Schur [[#References|[1]]]. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083480/s0834801.png" /> be the class of regular functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083480/s0834802.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083480/s0834803.png" /> satisfying in it the condition <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083480/s0834804.png" />. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083480/s0834805.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083480/s0834806.png" />, be the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083480/s0834807.png" />-dimensional complex Euclidean space, its points are <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083480/s0834808.png" />-tuples of complex numbers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083480/s0834809.png" />; let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083480/s08348010.png" /> be a set of points <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083480/s08348011.png" /> such that the numbers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083480/s08348012.png" /> are the first <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083480/s08348013.png" /> coefficients of some function from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083480/s08348014.png" />. The sets <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083480/s08348015.png" /> are closed, bounded and convex in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083480/s08348016.png" />. Then the following theorems hold. |
| − | s0834801.png | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | --> | ||
| − | + | Schur's first theorem: To the points <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083480/s08348017.png" /> on the boundary of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083480/s08348018.png" /> there correspond in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083480/s08348019.png" /> only rational functions of the form | |
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083480/s08348020.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | Schur's | + | Schur's second theorem: A necessary and sufficient condition for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083480/s08348021.png" /> to be an interior point of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083480/s08348022.png" /> is that the following inequalities hold for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083480/s08348023.png" />: |
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083480/s08348024.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Schur's second theorem provides the complete solution to the coefficient problem for bounded functions in the case of interior points of the coefficients region. | Schur's second theorem provides the complete solution to the coefficient problem for bounded functions in the case of interior points of the coefficients region. | ||
| Line 51: | Line 13: | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> I. Schur, "Ueber Potentzreihen, die im Innern des Einheitkreises berchränkt sind" ''J. Reine Angew. Math.'' , '''147''' (1917) pp. 205–232</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> L. Bieberbach, "Lehrbuch der Funktionentheorie" , '''2''' , Teubner (1931)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> G.M. Goluzin, "Geometric theory of functions of a complex variable" , ''Transl. Math. Monogr.'' , '''26''' , Amer. Math. Soc. (1969) (Translated from Russian)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> I. Schur, "Ueber Potentzreihen, die im Innern des Einheitkreises berchränkt sind" ''J. Reine Angew. Math.'' , '''147''' (1917) pp. 205–232</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> L. Bieberbach, "Lehrbuch der Funktionentheorie" , '''2''' , Teubner (1931)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> G.M. Goluzin, "Geometric theory of functions of a complex variable" , ''Transl. Math. Monogr.'' , '''26''' , Amer. Math. Soc. (1969) (Translated from Russian)</TD></TR></table> | ||
| + | |||
| + | |||
====Comments==== | ====Comments==== | ||
| + | |||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> P.L. Duren, "Univalent functions" , Springer (1983) pp. Sect. 10.11</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> J.B. Garnett, "Bounded analytic functions" , Acad. Press (1981) pp. 40</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> P.L. Duren, "Univalent functions" , Springer (1983) pp. Sect. 10.11</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> J.B. Garnett, "Bounded analytic functions" , Acad. Press (1981) pp. 40</TD></TR></table> | ||
Revision as of 14:53, 7 June 2020
Theorems for finding a solution to the coefficient problem for bounded analytic functions. They were obtained by I. Schur [1]. Let 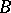 be the class of regular functions
be the class of regular functions  in
in 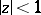 satisfying in it the condition
satisfying in it the condition 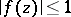 . Let
. Let 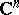 ,
, 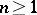 , be the
, be the  -dimensional complex Euclidean space, its points are
-dimensional complex Euclidean space, its points are  -tuples of complex numbers
-tuples of complex numbers  ; let
; let  be a set of points
be a set of points 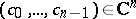 such that the numbers
such that the numbers  are the first
are the first  coefficients of some function from
coefficients of some function from 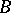 . The sets
. The sets  are closed, bounded and convex in
are closed, bounded and convex in 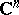 . Then the following theorems hold.
. Then the following theorems hold.
Schur's first theorem: To the points  on the boundary of
on the boundary of 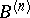 there correspond in
there correspond in 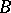 only rational functions of the form
only rational functions of the form
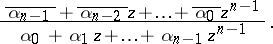 |
Schur's second theorem: A necessary and sufficient condition for 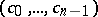 to be an interior point of
to be an interior point of  is that the following inequalities hold for
is that the following inequalities hold for 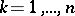 :
:
 |
Schur's second theorem provides the complete solution to the coefficient problem for bounded functions in the case of interior points of the coefficients region.
References
| [1] | I. Schur, "Ueber Potentzreihen, die im Innern des Einheitkreises berchränkt sind" J. Reine Angew. Math. , 147 (1917) pp. 205–232 |
| [2] | L. Bieberbach, "Lehrbuch der Funktionentheorie" , 2 , Teubner (1931) |
| [3] | G.M. Goluzin, "Geometric theory of functions of a complex variable" , Transl. Math. Monogr. , 26 , Amer. Math. Soc. (1969) (Translated from Russian) |
Comments
References
| [a1] | P.L. Duren, "Univalent functions" , Springer (1983) pp. Sect. 10.11 |
| [a2] | J.B. Garnett, "Bounded analytic functions" , Acad. Press (1981) pp. 40 |
Schur theorems. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Schur_theorems&oldid=48627