Namespaces
Variants
Actions

Difference between revisions of "Recursive predicate"

From Encyclopedia of Mathematics
Jump to: navigation, search
m (tex encoded by computer)
m (Undo revision 48459 by Ulf Rehmann (talk))
Tag: Undo
Line 1: Line 1:
−
<!--
+
A [[Predicate|predicate]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080300/r0803001.png" /> defined on the natural numbers, such that the function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080300/r0803002.png" /> defined on the natural numbers by the condition
−
r0803001.png
 
−
$#A+1 = 3 n = 0
 
−
$#C+1 = 3 : ~/encyclopedia/old_files/data/R080/R.0800300 Recursive predicate
 
−
Automatically converted into TeX, above some diagnostics.
 
−
Please remove this comment and the {{TEX|auto}} line below,
 
−
if TeX found to be correct.
 
−
-->
 
  
−
{{TEX|auto}}
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080300/r0803003.png" /></td> </tr></table>
−
{{TEX|done}}
 
−
 
 
−
A [[Predicate|predicate]]  $  P( x _ {1} \dots x _ {n} ) $
 
−
defined on the natural numbers, such that the function  $  f $
 
−
defined on the natural numbers by the condition
 
−
 
 
−
$$
 
−
f( x _ {1} \dots x _ {n} )  = \left \{
 
  
 
is a [[Recursive function|recursive function]].
 
is a [[Recursive function|recursive function]].

Revision as of 14:53, 7 June 2020

A predicate 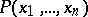defined on the natural numbers, such that the function 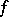defined on the natural numbers by the condition

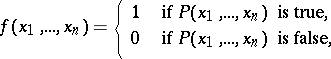is a recursive function.

How to Cite This Entry:
Recursive predicate. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Recursive_predicate&oldid=48459
This article was adapted from an original article by V.E. Plisko (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article
Retrieved from "https://encyclopediaofmath.org/index.php?title=Recursive_predicate&oldid=49395"