Difference between revisions of "Pauli matrices"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
Ulf Rehmann (talk | contribs) m (Undo revision 48144 by Ulf Rehmann (talk)) Tag: Undo |
||
| Line 1: | Line 1: | ||
| − | < | + | Certain special constant Hermitian <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071860/p0718601.png" />-matrices with complex entries. They were introduced by W. Pauli (1927) to describe spin (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071860/p0718602.png" />) and magnetic moment <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071860/p0718603.png" /> of an electron. His equation describes correctly in the non-relativistic case particles of spin 1/2 (in units <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071860/p0718604.png" />) and can be obtained from the [[Dirac equation|Dirac equation]] for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071860/p0718605.png" />. In explicit form the Pauli matrices are: |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071860/p0718606.png" /></td> </tr></table> | |
| − | |||
| − | + | Their eigen values are <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071860/p0718607.png" />. The Pauli matrices satisfy the following algebraic relations: | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071860/p0718608.png" /></td> </tr></table> | |
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071860/p0718609.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Together with the unit matrix | Together with the unit matrix | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071860/p07186010.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | the Pauli matrices form a complete system of second-order matrices by which an arbitrary linear operator (matrix) of dimension 2 can be expanded. They act on two-component spin functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071860/p07186011.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071860/p07186012.png" />, and are transformed under a rotation of the coordinate system by a linear two-valued representation of the rotation group. Under a rotation by an infinitesimal angle <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071860/p07186013.png" /> around an axis with a directed unit vector <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071860/p07186014.png" />, a spinor <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071860/p07186015.png" /> is transformed according to the formula | |
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071860/p07186016.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071860/p07186017.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | From the Pauli matrices one can form the [[Dirac matrices|Dirac matrices]] | + | From the Pauli matrices one can form the [[Dirac matrices|Dirac matrices]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071860/p07186018.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071860/p07186019.png" />: |
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071860/p07186020.png" /></td> </tr></table> | |
| − | |||
| − | The real linear combinations of | + | The real linear combinations of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071860/p07186021.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071860/p07186022.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071860/p07186023.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071860/p07186024.png" /> form a four-dimensional subalgebra of the algebra of complex <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071860/p07186025.png" />-matrices (under matrix multiplication) that is isomorphic to the simplest system of hypercomplex numbers, the quaternions, cf. [[Quaternion|Quaternion]]. They are used whenever an elementary particle has a discrete parameter taking only two values, for example, to describe an isospin nucleon (a proton-neutron). Quite generally, the Pauli matrices are used not only to describe isotopic space, but also in the formalism of the group of inner symmetries <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071860/p07186026.png" />. In this case they are generators of a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071860/p07186027.png" />-dimensional representation of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071860/p07186028.png" /> and are denoted by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071860/p07186029.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071860/p07186030.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071860/p07186031.png" />. Sometimes it is convenient to use the linear combinations |
| − | |||
| − | |||
| − | |||
| − | form a four-dimensional subalgebra of the algebra of complex | ||
| − | matrices (under matrix multiplication) that is isomorphic to the simplest system of hypercomplex numbers, the quaternions, cf. [[Quaternion|Quaternion]]. They are used whenever an elementary particle has a discrete parameter taking only two values, for example, to describe an isospin nucleon (a proton-neutron). Quite generally, the Pauli matrices are used not only to describe isotopic space, but also in the formalism of the group of inner symmetries | ||
| − | In this case they are generators of a | ||
| − | dimensional representation of | ||
| − | and are denoted by | ||
| − | |||
| − | and | ||
| − | Sometimes it is convenient to use the linear combinations | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071860/p07186032.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | In certain cases one introduces for a relativistically covariant description of two-component spinor functions instead of the Pauli matrices, matrices | + | In certain cases one introduces for a relativistically covariant description of two-component spinor functions instead of the Pauli matrices, matrices <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071860/p07186033.png" /> related by means of the following identities: |
| − | related by means of the following identities: | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071860/p07186034.png" /></td> <td valign="top" style="width:5%;text-align:right;">(1)</td></tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | where the symbol | + | where the symbol <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071860/p07186035.png" /> denotes complex conjugation. The matrices <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071860/p07186036.png" /> satisfy the commutator relations |
| − | denotes complex conjugation. The matrices | ||
| − | satisfy the commutator relations | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071860/p07186037.png" /></td> <td valign="top" style="width:5%;text-align:right;">(2)</td></tr></table> | |
| − | |||
| − | |||
| − | where | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071860/p07186038.png" /> are the components of the metric tensor of the Minkowski space of signature <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071860/p07186039.png" />. The formulas (1) and (2) make it possible to generalize the Pauli matrices covariantly to an arbitrary curved space: |
| − | are the components of the metric tensor of the Minkowski space of signature | ||
| − | The formulas (1) and (2) make it possible to generalize the Pauli matrices covariantly to an arbitrary curved space: | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071860/p07186040.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | where | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071860/p07186041.png" /> are the components of the metric tensor of the curved space. |
| − | are the components of the metric tensor of the curved space. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> W. Pauli, , ''Works on quantum theory'' , '''1–2''' , Moscow (1975–1977) (In Russian; translated from German)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> N.F. Nelina, "Physics of elementary particles" , Moscow (1977) (In Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> D. Bril, J.A. Wheeler, , ''The latest problems on gravitation'' , Moscow (1961) pp. 381–427 (In Russian)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> W. Pauli, , ''Works on quantum theory'' , '''1–2''' , Moscow (1975–1977) (In Russian; translated from German)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> N.F. Nelina, "Physics of elementary particles" , Moscow (1977) (In Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> D. Bril, J.A. Wheeler, , ''The latest problems on gravitation'' , Moscow (1961) pp. 381–427 (In Russian)</TD></TR></table> | ||
| + | |||
| + | |||
====Comments==== | ====Comments==== | ||
| + | |||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> W. Pauli, "Zur Quantenmechanik des magnetischen Elektrons" ''Z. Phys.'' , '''43''' : 601</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> W. Pauli (ed.) , ''Handbuch der Physik'' , '''24''' , Springer (1933)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> R.M. Wald, "General relativity" , Univ. Chicago Press (1984) pp. Chapt. 4</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> Y. Choquet-Bruhat, C. DeWitt-Morette, M. Dillard-Bleick, "Analysis, manifolds and physics" , North-Holland (1982) (Translated from French)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> W. Pauli, "Zur Quantenmechanik des magnetischen Elektrons" ''Z. Phys.'' , '''43''' : 601</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> W. Pauli (ed.) , ''Handbuch der Physik'' , '''24''' , Springer (1933)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> R.M. Wald, "General relativity" , Univ. Chicago Press (1984) pp. Chapt. 4</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> Y. Choquet-Bruhat, C. DeWitt-Morette, M. Dillard-Bleick, "Analysis, manifolds and physics" , North-Holland (1982) (Translated from French)</TD></TR></table> | ||
Revision as of 14:52, 7 June 2020
Certain special constant Hermitian 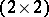 -matrices with complex entries. They were introduced by W. Pauli (1927) to describe spin (
-matrices with complex entries. They were introduced by W. Pauli (1927) to describe spin ( ) and magnetic moment
) and magnetic moment  of an electron. His equation describes correctly in the non-relativistic case particles of spin 1/2 (in units
of an electron. His equation describes correctly in the non-relativistic case particles of spin 1/2 (in units  ) and can be obtained from the Dirac equation for
) and can be obtained from the Dirac equation for 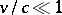 . In explicit form the Pauli matrices are:
. In explicit form the Pauli matrices are:
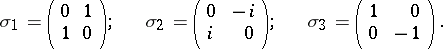 |
Their eigen values are 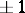 . The Pauli matrices satisfy the following algebraic relations:
. The Pauli matrices satisfy the following algebraic relations:
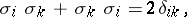 |
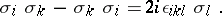 |
Together with the unit matrix
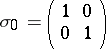 |
the Pauli matrices form a complete system of second-order matrices by which an arbitrary linear operator (matrix) of dimension 2 can be expanded. They act on two-component spin functions 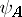 ,
, 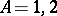 , and are transformed under a rotation of the coordinate system by a linear two-valued representation of the rotation group. Under a rotation by an infinitesimal angle
, and are transformed under a rotation of the coordinate system by a linear two-valued representation of the rotation group. Under a rotation by an infinitesimal angle 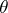 around an axis with a directed unit vector
around an axis with a directed unit vector 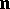 , a spinor
, a spinor 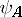 is transformed according to the formula
is transformed according to the formula
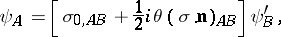 |
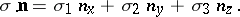 |
From the Pauli matrices one can form the Dirac matrices 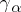 ,
, 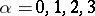 :
:
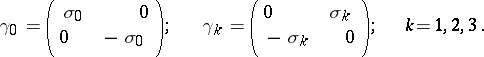 |
The real linear combinations of 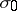 ,
,  ,
, 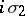 ,
, 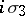 form a four-dimensional subalgebra of the algebra of complex
form a four-dimensional subalgebra of the algebra of complex 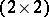 -matrices (under matrix multiplication) that is isomorphic to the simplest system of hypercomplex numbers, the quaternions, cf. Quaternion. They are used whenever an elementary particle has a discrete parameter taking only two values, for example, to describe an isospin nucleon (a proton-neutron). Quite generally, the Pauli matrices are used not only to describe isotopic space, but also in the formalism of the group of inner symmetries
-matrices (under matrix multiplication) that is isomorphic to the simplest system of hypercomplex numbers, the quaternions, cf. Quaternion. They are used whenever an elementary particle has a discrete parameter taking only two values, for example, to describe an isospin nucleon (a proton-neutron). Quite generally, the Pauli matrices are used not only to describe isotopic space, but also in the formalism of the group of inner symmetries 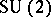 . In this case they are generators of a
. In this case they are generators of a  -dimensional representation of
-dimensional representation of  and are denoted by
and are denoted by 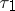 ,
,  and
and 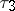 . Sometimes it is convenient to use the linear combinations
. Sometimes it is convenient to use the linear combinations
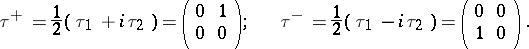 |
In certain cases one introduces for a relativistically covariant description of two-component spinor functions instead of the Pauli matrices, matrices 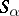 related by means of the following identities:
related by means of the following identities:
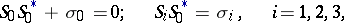 | (1) |
where the symbol  denotes complex conjugation. The matrices
denotes complex conjugation. The matrices 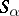 satisfy the commutator relations
satisfy the commutator relations
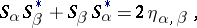 | (2) |
where 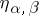 are the components of the metric tensor of the Minkowski space of signature
are the components of the metric tensor of the Minkowski space of signature 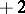 . The formulas (1) and (2) make it possible to generalize the Pauli matrices covariantly to an arbitrary curved space:
. The formulas (1) and (2) make it possible to generalize the Pauli matrices covariantly to an arbitrary curved space:
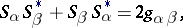 |
where 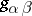 are the components of the metric tensor of the curved space.
are the components of the metric tensor of the curved space.
References
| [1] | W. Pauli, , Works on quantum theory , 1–2 , Moscow (1975–1977) (In Russian; translated from German) |
| [2] | N.F. Nelina, "Physics of elementary particles" , Moscow (1977) (In Russian) |
| [3] | D. Bril, J.A. Wheeler, , The latest problems on gravitation , Moscow (1961) pp. 381–427 (In Russian) |
Comments
References
| [a1] | W. Pauli, "Zur Quantenmechanik des magnetischen Elektrons" Z. Phys. , 43 : 601 |
| [a2] | W. Pauli (ed.) , Handbuch der Physik , 24 , Springer (1933) |
| [a3] | R.M. Wald, "General relativity" , Univ. Chicago Press (1984) pp. Chapt. 4 |
| [a4] | Y. Choquet-Bruhat, C. DeWitt-Morette, M. Dillard-Bleick, "Analysis, manifolds and physics" , North-Holland (1982) (Translated from French) |
Pauli matrices. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Pauli_matrices&oldid=48144