Namespaces
Variants
Actions

Difference between revisions of "Non-ideal relay"

From Encyclopedia of Mathematics
Jump to: navigation, search
m (tex encoded by computer)
m (Undo revision 47988 by Ulf Rehmann (talk))
Tag: Undo
Line 1: Line 1:
−
<!--
+
The [[Hysteresis|hysteresis]] non-linearity denoted by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110060/n1100601.png" />, with thresholds <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110060/n1100602.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110060/n1100603.png" />, and defined for a continuous input <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110060/n1100604.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110060/n1100605.png" />, and an initial state <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110060/n1100606.png" /> by the formulas (see Fig.a1.)
−
n1100601.png
 
−
$#A+1 = 19 n = 0
 
−
$#C+1 = 19 : ~/encyclopedia/old_files/data/N110/N.1100060 Non\AAhideal relay
 
−
Automatically converted into TeX, above some diagnostics.
 
−
Please remove this comment and the {{TEX|auto}} line below,
 
−
if TeX found to be correct.
 
−
-->
 
  
−
{{TEX|auto}}
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110060/n1100607.png" /></td> </tr></table>
−
{{TEX|done}}
 
  
−
The [[Hysteresis|hysteresis]] non-linearity denoted by  $  {\mathcal R} ( \alpha, \beta ) $,
+
where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110060/n1100608.png" />, that is, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110060/n1100609.png" /> denotes the last switching moment. The input–output operators <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110060/n11006010.png" /> are discontinuous in the usual function spaces. These operators are monotone in a natural sense, which allows one to use the powerful methods of the theory of semi-ordered spaces in the analysis of systems with non-ideal relays.
−
with thresholds  $  \alpha $
 
−
and  $  \beta $,
 
−
and defined for a continuous input  $  u ( t ) $,
 
−
$  t \geq  t _ {0} $,
 
−
and an initial state  $  r _ {0} \in \{ 0,1 \} $
 
−
by the formulas (see Fig.a1.)
 
−
 
 
−
$$
 
−
{\mathcal R} ( r _ {0} ; \alpha, \beta ) u ( t ) = \left \{
 
−
 
 
−
where $  \tau = \sup  \{ s : {s \leq  t, u ( s ) = \beta  \textrm{ or  }  u ( s ) = \alpha } \} $,  
 
−
that is, $  \tau $
 
−
denotes the last switching moment. The input–output operators $  {\mathcal R} ( r _ {0} ; \alpha, \beta ) $
 
−
are discontinuous in the usual function spaces. These operators are monotone in a natural sense, which allows one to use the powerful methods of the theory of semi-ordered spaces in the analysis of systems with non-ideal relays.
 
  
 
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/n110060a.gif" />
 
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/n110060a.gif" />
Line 33: Line 11:
 
Non-ideal relay
 
Non-ideal relay
  
−
The Preisach–Giltay model of ferromagnetic hysteresis is described as the spectral decomposition in a continual system of non-ideal relays in the following way. Let $  \mu ( \alpha, \beta ) $
+
The Preisach–Giltay model of ferromagnetic hysteresis is described as the spectral decomposition in a continual system of non-ideal relays in the following way. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110060/n11006011.png" /> be a finite [[Borel measure|Borel measure]] in the half-plane <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110060/n11006012.png" />. The input–output operators of the Preisach–Giltay hysteresis non-linearity at a given continuous input <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110060/n11006013.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110060/n11006014.png" />, and initial state <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110060/n11006015.png" /> is defined by the formula
−
be a finite [[Borel measure|Borel measure]] in the half-plane $  \Pi = \{ {( \alpha, \beta ) } : {\alpha > \beta } \} $.  
 
−
The input–output operators of the Preisach–Giltay hysteresis non-linearity at a given continuous input $  u ( t ) $,  
 
−
$  t \geq  t _ {0} $,  
 
−
and initial state $  S ( t _ {0} ) $
 
−
is defined by the formula
 
  
−
$$
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110060/n11006016.png" /></td> </tr></table>
−
x ( t ) = \int\limits { {\mathcal R} ( r _ {0} ( \alpha, \beta ) ; \alpha, \beta ) u ( t ) }  {d \mu ( \alpha, \beta ) } ,
 
−
$$
 
  
−
where the measurable function $  r _ {0} ( \alpha, \beta ) $
+
where the measurable function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110060/n11006017.png" /> describes the internal state of the non-linearity at the initial moment <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110060/n11006018.png" />. In contrast to the individual non-ideal relay, the operators of a Preisach–Giltay non-linearity are continuous in the space of continuous functions, provided that the measure <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110060/n11006019.png" /> is absolutely continuous with respect to the [[Lebesgue measure|Lebesgue measure]] (cf. [[Absolute continuity|Absolute continuity]]). For detailed properties of Preisach–Giltay hysteresis and further generalizations see [[#References|[a1]]], [[#References|[a2]]] and the references therein.
−
describes the internal state of the non-linearity at the initial moment $  t = t _ {0} $.  
 
−
In contrast to the individual non-ideal relay, the operators of a Preisach–Giltay non-linearity are continuous in the space of continuous functions, provided that the measure $  \mu ( \alpha, \beta ) $
 
−
is absolutely continuous with respect to the [[Lebesgue measure|Lebesgue measure]] (cf. [[Absolute continuity|Absolute continuity]]). For detailed properties of Preisach–Giltay hysteresis and further generalizations see [[#References|[a1]]], [[#References|[a2]]] and the references therein.
 
  
 
See also [[Hysteresis|Hysteresis]].
 
See also [[Hysteresis|Hysteresis]].

Revision as of 14:52, 7 June 2020

The hysteresis non-linearity denoted by , with thresholds and , and defined for a continuous input , , and an initial state by the formulas (see Fig.a1.)

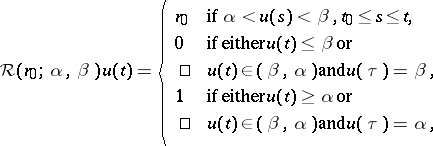where , that is, denotes the last switching moment. The input–output operators 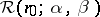are discontinuous in the usual function spaces. These operators are monotone in a natural sense, which allows one to use the powerful methods of the theory of semi-ordered spaces in the analysis of systems with non-ideal relays.

Figure: n110060a

Non-ideal relay

The Preisach–Giltay model of ferromagnetic hysteresis is described as the spectral decomposition in a continual system of non-ideal relays in the following way. Let be a finite Borel measure in the half-plane . The input–output operators of the Preisach–Giltay hysteresis non-linearity at a given continuous input , , and initial state is defined by the formula

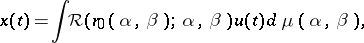where the measurable function describes the internal state of the non-linearity at the initial moment . In contrast to the individual non-ideal relay, the operators of a Preisach–Giltay non-linearity are continuous in the space of continuous functions, provided that the measure is absolutely continuous with respect to the Lebesgue measure (cf. Absolute continuity). For detailed properties of Preisach–Giltay hysteresis and further generalizations see [a1], [a2] and the references therein.

See also Hysteresis.

References

[a1] M.A. Krasnosel'skii, A.V. Pokrovskii, "Systems with hysteresis" , Springer (1989) (In Russian)
[a2] I.D. Mayergoyz, "Mathematical models of hysteresis" , Springer (1991)
How to Cite This Entry:
Non-ideal relay. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Non-ideal_relay&oldid=47988
This article was adapted from an original article by A.M. Krasnosel'skiiM.A. Krasnosel'skiiA.V. Pokrovskii (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article
Retrieved from "https://encyclopediaofmath.org/index.php?title=Non-ideal_relay&oldid=49331"