Difference between revisions of "Network"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
Ulf Rehmann (talk | contribs) m (Undo revision 47958 by Ulf Rehmann (talk)) Tag: Undo |
||
| Line 1: | Line 1: | ||
| − | + | A generalization of the idea of a [[Graph|graph]]. A network is defined by a pair <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n0663701.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n0663702.png" /> is a certain set and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n0663703.png" /> is a family of collection of elements from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n0663704.png" />. The elements in the sets <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n0663705.png" /> can, in general, be repeated. The elements of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n0663706.png" /> are called the vertices of the network, those of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n0663707.png" /> its poles and the collections <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n0663708.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n0663709.png" /> its edges. When the sets of poles is empty and each <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n06637010.png" /> is a set, a network is a [[Hypergraph|hypergraph]]. If each of the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n06637011.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n06637012.png" /> contains exactly two elements, the network is a graph with distinguished poles. Often, a network is regarded as a graph (with or without poles) to the elements of which are ascribed symbols from a certain set. For example, a graph with poles and such that to its edges are ascribed non-negative numbers, called channel capacities, is a transport network. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | A generalization of the idea of a [[Graph|graph]]. A network is defined by a pair | ||
| − | where | ||
| − | is a certain set and | ||
| − | is a family of collection of elements from | ||
| − | The elements in the sets | ||
| − | can, in general, be repeated. The elements of | ||
| − | are called the vertices of the network, those of | ||
| − | its poles and the collections | ||
| − | |||
| − | its edges. When the sets of poles is empty and each | ||
| − | is a set, a network is a [[Hypergraph|hypergraph]]. If each of the | ||
| − | |||
| − | contains exactly two elements, the network is a graph with distinguished poles. Often, a network is regarded as a graph (with or without poles) to the elements of which are ascribed symbols from a certain set. For example, a graph with poles and such that to its edges are ascribed non-negative numbers, called channel capacities, is a transport network. | ||
The concept of a network is used in the definition and description of a [[Control system|control system]] and of special classes of control systems (contact schemes, diagrams or functional elements), of transition diagrams of automata, communication networks, etc. | The concept of a network is used in the definition and description of a [[Control system|control system]] and of special classes of control systems (contact schemes, diagrams or functional elements), of transition diagrams of automata, communication networks, etc. | ||
| Line 29: | Line 5: | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> S.V. Yablonskii, "Fundamental concepts of cybernetics" ''Probl. Kibernet.'' , '''2''' (1959) pp. 7–38 (In Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> L.R. Ford, D.R. Fulkerson, "Flows in networks" , Princeton Univ. Press (1962)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> J. Kuntzmann, "Théorie des réseaux (graphes)" , Dunod (1972)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> S.V. Yablonskii, "Fundamental concepts of cybernetics" ''Probl. Kibernet.'' , '''2''' (1959) pp. 7–38 (In Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> L.R. Ford, D.R. Fulkerson, "Flows in networks" , Princeton Univ. Press (1962)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> J. Kuntzmann, "Théorie des réseaux (graphes)" , Dunod (1972)</TD></TR></table> | ||
| + | |||
| + | |||
====Comments==== | ====Comments==== | ||
For network in topology see [[Net (of sets in a topological space)|Net (of sets in a topological space)]]. | For network in topology see [[Net (of sets in a topological space)|Net (of sets in a topological space)]]. | ||
| − | Most often, a network is simply defined as a [[Graph|graph]] | + | Most often, a network is simply defined as a [[Graph|graph]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n06637013.png" /> such that for each <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n06637014.png" /> there is specified a (positive) number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n06637015.png" />, called the capacity of the edge <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n06637016.png" />. A directed network is a directed graph with for each <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n06637017.png" /> a specified capacity <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n06637018.png" />. Often <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n06637019.png" /> is thought of as the maximal amount of something that can be transported over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n06637020.png" />. But other interpretations are possible and occur. For example, a network of roads with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n06637021.png" /> length of road <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n06637022.png" /> for each <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n06637023.png" />. |
| − | such that for each | ||
| − | there is specified a (positive) number | ||
| − | called the capacity of the edge | ||
| − | A directed network is a directed graph with for each | ||
| − | a specified capacity | ||
| − | Often | ||
| − | is thought of as the maximal amount of something that can be transported over | ||
| − | But other interpretations are possible and occur. For example, a network of roads with | ||
| − | length of road | ||
| − | for each | ||
| − | A transportation network is a directed network with a specified vertex | + | A transportation network is a directed network with a specified vertex <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n06637024.png" />, the source, and a second specified vertex <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n06637025.png" />, the sink. Usually it is also assumed that there are no incoming arcs at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n06637026.png" /> and no outgoing arcs at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n06637027.png" />. For all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n06637028.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n06637029.png" />, let |
| − | the source, and a second specified vertex | ||
| − | the sink. Usually it is also assumed that there are no incoming arcs at | ||
| − | and no outgoing arcs at | ||
| − | For all | ||
| − | |||
| − | let | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n06637030.png" /></td> </tr></table> | |
| − | n | ||
| − | A flow in a transportation network is a function | + | A flow in a transportation network is a function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n06637031.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n06637032.png" /> and such that for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n06637033.png" /> the following Kirchhoff law holds: |
| − | such that | ||
| − | and such that for all | ||
| − | the following Kirchhoff law holds: | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n06637034.png" /></td> <td valign="top" style="width:5%;text-align:right;">(a1)</td></tr></table> | |
| − | |||
| − | |||
| − | Sometimes an artificial arc, the return arc, going from | + | Sometimes an artificial arc, the return arc, going from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n06637035.png" /> to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n06637036.png" />, is added with capacity <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n06637037.png" />. By defining <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n06637038.png" />, a flow is defined such that the Kirchhoff law holds for all vertices. This is the sole function of the return arc. |
| − | to | ||
| − | is added with capacity | ||
| − | By defining | ||
| − | a flow is defined such that the Kirchhoff law holds for all vertices. This is the sole function of the return arc. | ||
| − | The network flow problem addresses the problem of calculating those flows for which | + | The network flow problem addresses the problem of calculating those flows for which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n06637039.png" /> is maximal. |
| − | is maximal. | ||
| − | In [[Network planning|network planning]] one encounters "transportation networks" in which the edges correspond to tasks which can be performed and where the numbers | + | In [[Network planning|network planning]] one encounters "transportation networks" in which the edges correspond to tasks which can be performed and where the numbers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n06637040.png" /> represent, for example, the time needed to perform task <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n06637041.png" />. Here, finding a "shortest path" can be important. |
| − | represent, for example, the time needed to perform task | ||
| − | Here, finding a "shortest path" can be important. | ||
| − | An electrical network is a directed graph with for each | + | An electrical network is a directed graph with for each <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n06637042.png" /> two real numbers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n06637043.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n06637044.png" /> specified (which are thought of as current and voltage, respectively). More generally, the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n06637045.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n06637046.png" /> may well be functions of time or variables. |
| − | two real numbers | ||
| − | and | ||
| − | specified (which are thought of as current and voltage, respectively). More generally, the | ||
| − | and | ||
| − | may well be functions of time or variables. | ||
| − | The currents | + | The currents <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n06637047.png" /> are required to satisfy the Kirchhoff current law |
| − | are required to satisfy the Kirchhoff current law | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n06637048.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | and the voltages | + | and the voltages <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n06637049.png" /> are required to satisfy the Kirchhoff voltage law, which says that there are numbers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n06637050.png" />, the potential at node <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n06637051.png" />, such that |
| − | are required to satisfy the Kirchhoff voltage law, which says that there are numbers | ||
| − | the potential at node | ||
| − | such that | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n06637052.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | A branch (edge) of a network in which the current is given as an (input) function of time is called a current source, and a branch over which there is given an voltage is called a voltage source. A branch which is either a voltage or a current source is called a source branch. An electrical network with | + | A branch (edge) of a network in which the current is given as an (input) function of time is called a current source, and a branch over which there is given an voltage is called a voltage source. A branch which is either a voltage or a current source is called a source branch. An electrical network with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n06637053.png" /> specified source branches is called an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n06637055.png" />-port. |
| − | specified source branches is called an | ||
| − | port. | ||
If the currents in and the voltages across the (non-source) branches are related by | If the currents in and the voltages across the (non-source) branches are related by | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n06637056.png" /></td> </tr></table> | |
| − | |||
| − | |||
or | or | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n06637057.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | where the | + | where the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n06637058.png" /> or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n06637059.png" /> are linear integro-differential operators, one speaks of a linear electrical network. It is called reciprocal if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n06637060.png" /> or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n06637061.png" />. The network is called passive if |
| − | or | ||
| − | are linear integro-differential operators, one speaks of a linear electrical network. It is called reciprocal if | ||
| − | or | ||
| − | The network is called passive if | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n06637062.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | for all choices of the current sources and voltage sources for which the current/voltage relations are satisfied. Here | + | for all choices of the current sources and voltage sources for which the current/voltage relations are satisfied. Here <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n06637063.png" /> denotes the set of source branches. |
| − | denotes the set of source branches. | ||
Under certain non-singularity conditions for the currents in and voltages across the source branches one has the relations | Under certain non-singularity conditions for the currents in and voltages across the source branches one has the relations | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n06637064.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n06637065.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | The matrices | + | The matrices <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n06637066.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n06637067.png" /> are, respectively, called the port-impedance matrix and the port-admittance matrix of the network. |
| − | and | ||
| − | are, respectively, called the port-impedance matrix and the port-admittance matrix of the network. | ||
| − | Synthesis of electrical networks, or realizability theory, refers to the problem of finding an electrical network with (partly) given port-impedance and port-admittance matrices. Every passive linear one-port network can be realized using as branches positive resistors | + | Synthesis of electrical networks, or realizability theory, refers to the problem of finding an electrical network with (partly) given port-impedance and port-admittance matrices. Every passive linear one-port network can be realized using as branches positive resistors <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n06637068.png" />, positive capacitators <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n06637069.png" /> and positive inductors <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n06637070.png" />. Every linear passive <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n06637071.png" />-port with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n06637072.png" /> can be synthesized using in addition ideal transformers (a pair of branches <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n06637073.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n06637074.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n06637075.png" />) and ideal gyrators (a pair of branches <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n06637076.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n06637077.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066370/n06637078.png" />). |
| − | positive capacitators | ||
| − | and positive inductors | ||
| − | Every linear passive | ||
| − | port with | ||
| − | can be synthesized using in addition ideal transformers (a pair of branches | ||
| − | such that | ||
| − | |||
| − | and ideal gyrators (a pair of branches | ||
| − | such that | ||
| − | |||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> L. Weinberg, "Network analysis and synthesis" , McGraw-Hill (1962)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> O. Brune, "Synthesis of a finite two-terminal network whose driving-point impedance is a prescribed function of frequency" ''J. Math. Phys.'' , '''10''' (1931) pp. 191–236</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> C.H. Papadimitriou, K. Steiglitz, "Combinatorial optimization. Algorithms and complexity" , Prentice-Hall (1982)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> D.R. Fulkerson, "Flow networks and combinatorial operations research" D.R. Fulkerson (ed.) , ''Studies in graph theory'' , '''I''' , Math. Assoc. Amer. (1975) pp. 139–171</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> C. Berge, "Graphs" , North-Holland (1985) pp. Chapt. 5</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> G.I. Atebekov, "Linear network theory" , Pergamon (1965)</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> P. Slepian, "Foundations of network analysis" , Springer (1968)</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> N.K. Bose, "Applied multidimensional system theory" , v. Nostrand-Reinhold (1982) pp. Chapt. 5</TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> A. Budak, "Circuit theory. Fundamentals and applications" , Prentice-Hall (1978)</TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> M. Gondran, M. Minoux, "Graphs and algorithms" , Wiley (1986) pp. Chapt. 5 (Translated from French)</TD></TR><TR><TD valign="top">[a11]</TD> <TD valign="top"> S.A. Burr (ed.) , ''The mathematics of networks'' , Amer. Math. Soc. (1982)</TD></TR><TR><TD valign="top">[a12]</TD> <TD valign="top"> C.W. Cox, "Circuits, signals and networks" , Macmillan (1969)</TD></TR><TR><TD valign="top">[a13]</TD> <TD valign="top"> B. Carré, "Graphs and networks" , Clarendon Press (1979)</TD></TR><TR><TD valign="top">[a14]</TD> <TD valign="top"> R.G. Busacker, T.L. Saaty, "Finite graphs and networks" , McGraw-Hill (1965)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> L. Weinberg, "Network analysis and synthesis" , McGraw-Hill (1962)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> O. Brune, "Synthesis of a finite two-terminal network whose driving-point impedance is a prescribed function of frequency" ''J. Math. Phys.'' , '''10''' (1931) pp. 191–236</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> C.H. Papadimitriou, K. Steiglitz, "Combinatorial optimization. Algorithms and complexity" , Prentice-Hall (1982)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> D.R. Fulkerson, "Flow networks and combinatorial operations research" D.R. Fulkerson (ed.) , ''Studies in graph theory'' , '''I''' , Math. Assoc. Amer. (1975) pp. 139–171</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> C. Berge, "Graphs" , North-Holland (1985) pp. Chapt. 5</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> G.I. Atebekov, "Linear network theory" , Pergamon (1965)</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> P. Slepian, "Foundations of network analysis" , Springer (1968)</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> N.K. Bose, "Applied multidimensional system theory" , v. Nostrand-Reinhold (1982) pp. Chapt. 5</TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> A. Budak, "Circuit theory. Fundamentals and applications" , Prentice-Hall (1978)</TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> M. Gondran, M. Minoux, "Graphs and algorithms" , Wiley (1986) pp. Chapt. 5 (Translated from French)</TD></TR><TR><TD valign="top">[a11]</TD> <TD valign="top"> S.A. Burr (ed.) , ''The mathematics of networks'' , Amer. Math. Soc. (1982)</TD></TR><TR><TD valign="top">[a12]</TD> <TD valign="top"> C.W. Cox, "Circuits, signals and networks" , Macmillan (1969)</TD></TR><TR><TD valign="top">[a13]</TD> <TD valign="top"> B. Carré, "Graphs and networks" , Clarendon Press (1979)</TD></TR><TR><TD valign="top">[a14]</TD> <TD valign="top"> R.G. Busacker, T.L. Saaty, "Finite graphs and networks" , McGraw-Hill (1965)</TD></TR></table> | ||
Revision as of 14:32, 7 June 2020
A generalization of the idea of a graph. A network is defined by a pair  , where
, where  is a certain set and
is a certain set and  is a family of collection of elements from
is a family of collection of elements from  . The elements in the sets
. The elements in the sets  can, in general, be repeated. The elements of
can, in general, be repeated. The elements of  are called the vertices of the network, those of
are called the vertices of the network, those of  its poles and the collections
its poles and the collections  ,
,  its edges. When the sets of poles is empty and each
its edges. When the sets of poles is empty and each  is a set, a network is a hypergraph. If each of the
is a set, a network is a hypergraph. If each of the 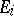 ,
,  contains exactly two elements, the network is a graph with distinguished poles. Often, a network is regarded as a graph (with or without poles) to the elements of which are ascribed symbols from a certain set. For example, a graph with poles and such that to its edges are ascribed non-negative numbers, called channel capacities, is a transport network.
contains exactly two elements, the network is a graph with distinguished poles. Often, a network is regarded as a graph (with or without poles) to the elements of which are ascribed symbols from a certain set. For example, a graph with poles and such that to its edges are ascribed non-negative numbers, called channel capacities, is a transport network.
The concept of a network is used in the definition and description of a control system and of special classes of control systems (contact schemes, diagrams or functional elements), of transition diagrams of automata, communication networks, etc.
References
| [1] | S.V. Yablonskii, "Fundamental concepts of cybernetics" Probl. Kibernet. , 2 (1959) pp. 7–38 (In Russian) |
| [2] | L.R. Ford, D.R. Fulkerson, "Flows in networks" , Princeton Univ. Press (1962) |
| [3] | J. Kuntzmann, "Théorie des réseaux (graphes)" , Dunod (1972) |
Comments
For network in topology see Net (of sets in a topological space).
Most often, a network is simply defined as a graph 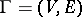 such that for each
such that for each 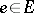 there is specified a (positive) number
there is specified a (positive) number 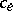 , called the capacity of the edge
, called the capacity of the edge  . A directed network is a directed graph with for each
. A directed network is a directed graph with for each 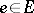 a specified capacity
a specified capacity  . Often
. Often 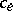 is thought of as the maximal amount of something that can be transported over
is thought of as the maximal amount of something that can be transported over  . But other interpretations are possible and occur. For example, a network of roads with
. But other interpretations are possible and occur. For example, a network of roads with 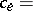 length of road
length of road  for each
for each  .
.
A transportation network is a directed network with a specified vertex 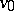 , the source, and a second specified vertex
, the source, and a second specified vertex 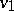 , the sink. Usually it is also assumed that there are no incoming arcs at
, the sink. Usually it is also assumed that there are no incoming arcs at  and no outgoing arcs at
and no outgoing arcs at 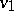 . For all
. For all 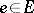 ,
, 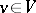 , let
, let
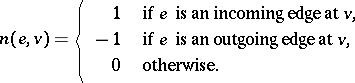 |
A flow in a transportation network is a function  such that
such that 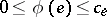 and such that for all
and such that for all 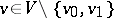 the following Kirchhoff law holds:
the following Kirchhoff law holds:
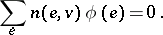 | (a1) |
Sometimes an artificial arc, the return arc, going from 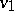 to
to 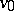 , is added with capacity
, is added with capacity 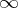 . By defining
. By defining 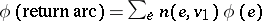 , a flow is defined such that the Kirchhoff law holds for all vertices. This is the sole function of the return arc.
, a flow is defined such that the Kirchhoff law holds for all vertices. This is the sole function of the return arc.
The network flow problem addresses the problem of calculating those flows for which  is maximal.
is maximal.
In network planning one encounters "transportation networks" in which the edges correspond to tasks which can be performed and where the numbers 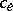 represent, for example, the time needed to perform task
represent, for example, the time needed to perform task  . Here, finding a "shortest path" can be important.
. Here, finding a "shortest path" can be important.
An electrical network is a directed graph with for each 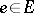 two real numbers
two real numbers 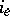 and
and 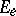 specified (which are thought of as current and voltage, respectively). More generally, the
specified (which are thought of as current and voltage, respectively). More generally, the 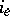 and
and 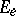 may well be functions of time or variables.
may well be functions of time or variables.
The currents 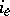 are required to satisfy the Kirchhoff current law
are required to satisfy the Kirchhoff current law
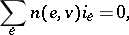 |
and the voltages 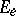 are required to satisfy the Kirchhoff voltage law, which says that there are numbers
are required to satisfy the Kirchhoff voltage law, which says that there are numbers 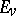 , the potential at node
, the potential at node  , such that
, such that
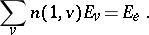 |
A branch (edge) of a network in which the current is given as an (input) function of time is called a current source, and a branch over which there is given an voltage is called a voltage source. A branch which is either a voltage or a current source is called a source branch. An electrical network with  specified source branches is called an
specified source branches is called an  -port.
-port.
If the currents in and the voltages across the (non-source) branches are related by
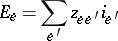 |
or
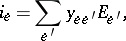 |
where the 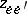 or
or  are linear integro-differential operators, one speaks of a linear electrical network. It is called reciprocal if
are linear integro-differential operators, one speaks of a linear electrical network. It is called reciprocal if 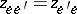 or
or  . The network is called passive if
. The network is called passive if
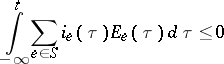 |
for all choices of the current sources and voltage sources for which the current/voltage relations are satisfied. Here 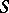 denotes the set of source branches.
denotes the set of source branches.
Under certain non-singularity conditions for the currents in and voltages across the source branches one has the relations
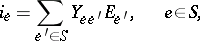 |
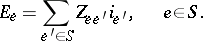 |
The matrices 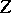 and
and 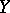 are, respectively, called the port-impedance matrix and the port-admittance matrix of the network.
are, respectively, called the port-impedance matrix and the port-admittance matrix of the network.
Synthesis of electrical networks, or realizability theory, refers to the problem of finding an electrical network with (partly) given port-impedance and port-admittance matrices. Every passive linear one-port network can be realized using as branches positive resistors  , positive capacitators
, positive capacitators  and positive inductors
and positive inductors 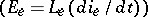 . Every linear passive
. Every linear passive  -port with
-port with 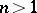 can be synthesized using in addition ideal transformers (a pair of branches
can be synthesized using in addition ideal transformers (a pair of branches 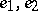 such that
such that 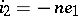 ,
,  ) and ideal gyrators (a pair of branches
) and ideal gyrators (a pair of branches 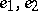 such that
such that  ,
,  ).
).
References
| [a1] | L. Weinberg, "Network analysis and synthesis" , McGraw-Hill (1962) |
| [a2] | O. Brune, "Synthesis of a finite two-terminal network whose driving-point impedance is a prescribed function of frequency" J. Math. Phys. , 10 (1931) pp. 191–236 |
| [a3] | C.H. Papadimitriou, K. Steiglitz, "Combinatorial optimization. Algorithms and complexity" , Prentice-Hall (1982) |
| [a4] | D.R. Fulkerson, "Flow networks and combinatorial operations research" D.R. Fulkerson (ed.) , Studies in graph theory , I , Math. Assoc. Amer. (1975) pp. 139–171 |
| [a5] | C. Berge, "Graphs" , North-Holland (1985) pp. Chapt. 5 |
| [a6] | G.I. Atebekov, "Linear network theory" , Pergamon (1965) |
| [a7] | P. Slepian, "Foundations of network analysis" , Springer (1968) |
| [a8] | N.K. Bose, "Applied multidimensional system theory" , v. Nostrand-Reinhold (1982) pp. Chapt. 5 |
| [a9] | A. Budak, "Circuit theory. Fundamentals and applications" , Prentice-Hall (1978) |
| [a10] | M. Gondran, M. Minoux, "Graphs and algorithms" , Wiley (1986) pp. Chapt. 5 (Translated from French) |
| [a11] | S.A. Burr (ed.) , The mathematics of networks , Amer. Math. Soc. (1982) |
| [a12] | C.W. Cox, "Circuits, signals and networks" , Macmillan (1969) |
| [a13] | B. Carré, "Graphs and networks" , Clarendon Press (1979) |
| [a14] | R.G. Busacker, T.L. Saaty, "Finite graphs and networks" , McGraw-Hill (1965) |
Network. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Network&oldid=47958