Difference between revisions of "Method of extensions and restrictions"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
Ulf Rehmann (talk | contribs) m (Undo revision 47826 by Ulf Rehmann (talk)) Tag: Undo |
||
| Line 1: | Line 1: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
''method of prolongations and restrictions'' | ''method of prolongations and restrictions'' | ||
A method for studying various differential-geometric structures (cf. [[Differential-geometric structure|Differential-geometric structure]]) on smooth manifolds and their submanifolds. At the basis of this method there lies a differential-algebraic criterion for an operation that allows one to associate in an invariant (coordinate-free) way to a given structure structures intrinsically related to it, among them their differential invariants (cf. [[Differential invariant|Differential invariant]]). Historically this method arose as a consequence of the [[Moving-frame method|moving-frame method]] as an invariant method for studying submanifolds of homogeneous spaces or of spaces with a connection. Subsequently the method of prolongations and restrictions was extended to the geometry of arbitrary fibre spaces (cf. [[Fibre space|Fibre space]]). In distinction from the aim of the moving-frame method — to construct a canonical field of frames and differential invariants of the unknown structure by means of subsequent restriction of corresponding principal fibre spaces — the method of prolongations and restrictions has as its aim the construction of invariants and invariantly associated structures without restricting the principal fibres of frames. The process of canonization of a frame is included in the method of prolongations and restrictions. | A method for studying various differential-geometric structures (cf. [[Differential-geometric structure|Differential-geometric structure]]) on smooth manifolds and their submanifolds. At the basis of this method there lies a differential-algebraic criterion for an operation that allows one to associate in an invariant (coordinate-free) way to a given structure structures intrinsically related to it, among them their differential invariants (cf. [[Differential invariant|Differential invariant]]). Historically this method arose as a consequence of the [[Moving-frame method|moving-frame method]] as an invariant method for studying submanifolds of homogeneous spaces or of spaces with a connection. Subsequently the method of prolongations and restrictions was extended to the geometry of arbitrary fibre spaces (cf. [[Fibre space|Fibre space]]). In distinction from the aim of the moving-frame method — to construct a canonical field of frames and differential invariants of the unknown structure by means of subsequent restriction of corresponding principal fibre spaces — the method of prolongations and restrictions has as its aim the construction of invariants and invariantly associated structures without restricting the principal fibres of frames. The process of canonization of a frame is included in the method of prolongations and restrictions. | ||
| − | Let | + | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m0635901.png" /> be a [[Lie group|Lie group]] and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m0635902.png" /> be the class of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m0635903.png" />-spaces with a left action of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m0635904.png" /> as transformation group on them. A <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m0635906.png" />-restriction is a smooth surjective mapping |
| − | be a [[Lie group|Lie group]] and let | ||
| − | be the class of | ||
| − | spaces with a left action of | ||
| − | as transformation group on them. A | ||
| − | restriction is a smooth surjective mapping | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m0635907.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | such that for any | + | such that for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m0635908.png" /> the following diagram is commutative: |
| − | the following diagram is commutative: | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m0635909.png" /></td> </tr></table> | |
| − | Here | + | Here <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359010.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359011.png" /> are the transformations of the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359012.png" />-spaces <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359013.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359014.png" />, respectively, determined by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359015.png" />. In this case one says that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359016.png" /> is a restriction of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359018.png" /> by means of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359019.png" />, or that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359020.png" /> is a prolongation of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359022.png" />. The class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359023.png" /> becomes a category with the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359024.png" />-restrictions as morphisms. |
| − | and | ||
| − | are the transformations of the | ||
| − | spaces | ||
| − | and | ||
| − | respectively, determined by | ||
| − | In this case one says that | ||
| − | is a restriction of | ||
| − | by means of | ||
| − | or that | ||
| − | is a prolongation of | ||
| − | The class | ||
| − | becomes a category with the | ||
| − | restrictions as morphisms. | ||
| − | Examples of | + | Examples of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359026.png" />-restrictions. |
| − | restrictions. | ||
| − | 1) Let | + | 1) Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359027.png" /> be the space of tensors of type <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359028.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359029.png" />. The contraction mapping |
| − | be the space of tensors of type | ||
| − | |||
| − | The contraction mapping | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359030.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | is a restriction. The complete contraction of tensors of | + | is a restriction. The complete contraction of tensors of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359031.png" />, |
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359032.png" /></td> </tr></table> | |
| − | |||
| − | |||
is an example of a restriction invariant. | is an example of a restriction invariant. | ||
| − | 2) If | + | 2) If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359033.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359034.png" /> restricts by means of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359035.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359036.png" />, respectively, to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359037.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359038.png" />. In other words, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359039.png" /> is a prolongation of both <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359040.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359041.png" />. |
| − | then | ||
| − | restricts by means of | ||
| − | and | ||
| − | respectively, to | ||
| − | and | ||
| − | In other words, | ||
| − | is a prolongation of both | ||
| − | and | ||
| − | The concept of a restriction can be naturally generalized to classes of fibre spaces associated with principal fibre bundles. Let | + | The concept of a restriction can be naturally generalized to classes of fibre spaces associated with principal fibre bundles. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359042.png" /> be a principal fibre bundle with structure group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359043.png" />, acting on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359044.png" /> from the right, and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359045.png" /> be a left <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359046.png" />-space. Fibre spaces associated with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359047.png" /> by objects from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359048.png" /> are spaces of the type |
| − | be a principal fibre bundle with structure group | ||
| − | acting on | ||
| − | from the right, and let | ||
| − | be a left | ||
| − | space. Fibre spaces associated with | ||
| − | by objects from | ||
| − | are spaces of the type | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359049.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | where factorization is by the following right action of | + | where factorization is by the following right action of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359050.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359051.png" />: |
| − | on | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359052.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | The space | + | The space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359053.png" /> is a fibre bundle over the base <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359054.png" /> with typical fibre <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359055.png" />. The element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359056.png" /> determined by a pair <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359057.png" /> is written as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359058.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359059.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359060.png" /> is an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359061.png" />-restriction mapping, then, by construction, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359062.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359063.png" /> induce a fibre-wise surjective mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359064.png" />, called a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359066.png" />-restriction. The <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359067.png" />-restriction <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359068.png" /> is defined by |
| − | is a fibre bundle over the base | ||
| − | with typical fibre | ||
| − | The element | ||
| − | determined by a pair | ||
| − | is written as | ||
| − | If | ||
| − | and | ||
| − | is an | ||
| − | restriction mapping, then, by construction, | ||
| − | and | ||
| − | induce a fibre-wise surjective mapping | ||
| − | called a | ||
| − | restriction. The | ||
| − | restriction | ||
| − | is defined by | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359069.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | Thus, the class | + | Thus, the class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359070.png" /> of fibre bundles associated with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359071.png" /> is a category with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359072.png" />-restrictions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359073.png" /> as morphisms. The correspondence <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359074.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359075.png" /> is a bijective functor from the category <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359076.png" /> to the category <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359077.png" />. Hence it is sufficient to study the restriction operation in the category of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359078.png" />-spaces. |
| − | of fibre bundles associated with | ||
| − | is a category with | ||
| − | restrictions | ||
| − | as morphisms. The correspondence | ||
| − | |||
| − | is a bijective functor from the category | ||
| − | to the category | ||
| − | Hence it is sufficient to study the restriction operation in the category of | ||
| − | spaces. | ||
| − | If | + | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359079.png" /> is a section of a fibre bundle <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359080.png" /> (a field of geometric objects of type <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359081.png" />), then the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359082.png" />-restriction <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359083.png" /> associates the section <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359084.png" /> of the restricted fibre bundle <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359085.png" /> to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359086.png" />. In other words, the field of geometric objects <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359087.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359088.png" />, restricts the field of geometric objects <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359089.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359090.png" /> is the structure object of a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359091.png" />-structure, then the study of the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063590/m06359092.png" />-structures and its invariants reduces largely to the search for restricting geometric objects. In the latter process, an important role is played by differential criteria for restrictions, formulated in terms of structure differential forms of fibre spaces forming the base of the method of restrictions and prolongations. |
| − | is a section of a fibre bundle | ||
| − | a field of geometric objects of type | ||
| − | then the | ||
| − | restriction | ||
| − | associates the section | ||
| − | of the restricted fibre bundle | ||
| − | to | ||
| − | In other words, the field of geometric objects | ||
| − | |||
| − | restricts the field of geometric objects | ||
| − | If | ||
| − | is the structure object of a | ||
| − | structure, then the study of the | ||
| − | structures and its invariants reduces largely to the search for restricting geometric objects. In the latter process, an important role is played by differential criteria for restrictions, formulated in terms of structure differential forms of fibre spaces forming the base of the method of restrictions and prolongations. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> G.F. Laptev, "Differential geometry of imbedded manifolds. Group-theoretical method of differential-geometric investigation" ''Trudy Moskov. Mat. Obshch.'' , '''2''' (1953) pp. 275–382 (In Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> G.F. Laptev, , ''Proc. 3-rd All-Union Mat. Congress (Moscow, 1956)'' , '''3''' , Moscow (1958) pp. 409–418</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> G.F. Laptev, "Differential geometry of imbedded manifolds. Group-theoretical method of differential-geometric investigation" ''Trudy Moskov. Mat. Obshch.'' , '''2''' (1953) pp. 275–382 (In Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> G.F. Laptev, , ''Proc. 3-rd All-Union Mat. Congress (Moscow, 1956)'' , '''3''' , Moscow (1958) pp. 409–418</TD></TR></table> | ||
| + | |||
| + | |||
====Comments==== | ====Comments==== | ||
| + | |||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> G. Jensen, "Higher order contact of submanifolds of homogeneous spaces" , ''Lect. notes in math.'' , '''610''' , Springer (1977)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> S. Kobayashi, K. Nomizu, "Foundations of differential geometry" , '''1–2''' , Interscience (1979)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> G. Jensen, "Higher order contact of submanifolds of homogeneous spaces" , ''Lect. notes in math.'' , '''610''' , Springer (1977)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> S. Kobayashi, K. Nomizu, "Foundations of differential geometry" , '''1–2''' , Interscience (1979)</TD></TR></table> | ||
Revision as of 10:26, 7 June 2020
method of prolongations and restrictions
A method for studying various differential-geometric structures (cf. Differential-geometric structure) on smooth manifolds and their submanifolds. At the basis of this method there lies a differential-algebraic criterion for an operation that allows one to associate in an invariant (coordinate-free) way to a given structure structures intrinsically related to it, among them their differential invariants (cf. Differential invariant). Historically this method arose as a consequence of the moving-frame method as an invariant method for studying submanifolds of homogeneous spaces or of spaces with a connection. Subsequently the method of prolongations and restrictions was extended to the geometry of arbitrary fibre spaces (cf. Fibre space). In distinction from the aim of the moving-frame method — to construct a canonical field of frames and differential invariants of the unknown structure by means of subsequent restriction of corresponding principal fibre spaces — the method of prolongations and restrictions has as its aim the construction of invariants and invariantly associated structures without restricting the principal fibres of frames. The process of canonization of a frame is included in the method of prolongations and restrictions.
Let 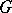 be a Lie group and let
be a Lie group and let 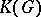 be the class of
be the class of 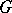 -spaces with a left action of
-spaces with a left action of  as transformation group on them. A
as transformation group on them. A 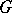 -restriction is a smooth surjective mapping
-restriction is a smooth surjective mapping
 |
such that for any 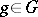 the following diagram is commutative:
the following diagram is commutative:
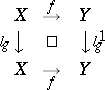 |
Here 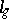 and
and 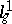 are the transformations of the
are the transformations of the 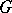 -spaces
-spaces 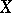 and
and 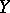 , respectively, determined by
, respectively, determined by 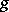 . In this case one says that
. In this case one says that 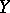 is a restriction of
is a restriction of 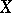 by means of
by means of 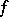 , or that
, or that 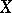 is a prolongation of
is a prolongation of 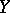 . The class
. The class 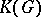 becomes a category with the
becomes a category with the 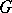 -restrictions as morphisms.
-restrictions as morphisms.
Examples of 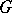 -restrictions.
-restrictions.
1) Let  be the space of tensors of type
be the space of tensors of type 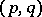 ,
,  . The contraction mapping
. The contraction mapping
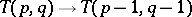 |
is a restriction. The complete contraction of tensors of  ,
,
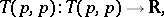 |
is an example of a restriction invariant.
2) If 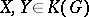 , then
, then 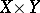 restricts by means of
restricts by means of 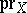 and
and 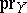 , respectively, to
, respectively, to 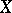 and
and 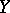 . In other words,
. In other words, 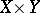 is a prolongation of both
is a prolongation of both 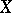 and
and 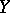 .
.
The concept of a restriction can be naturally generalized to classes of fibre spaces associated with principal fibre bundles. Let 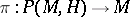 be a principal fibre bundle with structure group
be a principal fibre bundle with structure group 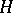 , acting on
, acting on 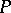 from the right, and let
from the right, and let 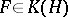 be a left
be a left 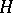 -space. Fibre spaces associated with
-space. Fibre spaces associated with 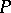 by objects from
by objects from 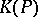 are spaces of the type
are spaces of the type
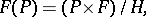 |
where factorization is by the following right action of 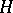 on
on 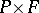 :
:
 |
The space 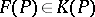 is a fibre bundle over the base
is a fibre bundle over the base 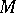 with typical fibre
with typical fibre 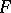 . The element
. The element 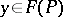 determined by a pair
determined by a pair 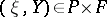 is written as
is written as 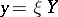 . If
. If 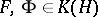 and
and 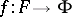 is an
is an 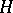 -restriction mapping, then, by construction,
-restriction mapping, then, by construction, 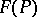 and
and 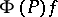 induce a fibre-wise surjective mapping
induce a fibre-wise surjective mapping  , called a
, called a 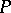 -restriction. The
-restriction. The 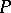 -restriction
-restriction 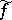 is defined by
is defined by
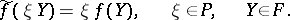 |
Thus, the class 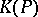 of fibre bundles associated with
of fibre bundles associated with 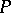 is a category with
is a category with 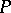 -restrictions
-restrictions 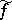 as morphisms. The correspondence
as morphisms. The correspondence 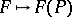 ,
, 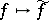 is a bijective functor from the category
is a bijective functor from the category 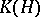 to the category
to the category 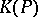 . Hence it is sufficient to study the restriction operation in the category of
. Hence it is sufficient to study the restriction operation in the category of 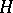 -spaces.
-spaces.
If 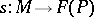 is a section of a fibre bundle
is a section of a fibre bundle 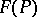 (a field of geometric objects of type
(a field of geometric objects of type 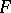 ), then the
), then the  -restriction
-restriction 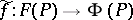 associates the section
associates the section 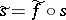 of the restricted fibre bundle
of the restricted fibre bundle 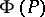 to
to  . In other words, the field of geometric objects
. In other words, the field of geometric objects 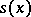 ,
, 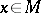 , restricts the field of geometric objects
, restricts the field of geometric objects 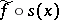 . If
. If 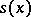 is the structure object of a
is the structure object of a 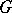 -structure, then the study of the
-structure, then the study of the 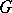 -structures and its invariants reduces largely to the search for restricting geometric objects. In the latter process, an important role is played by differential criteria for restrictions, formulated in terms of structure differential forms of fibre spaces forming the base of the method of restrictions and prolongations.
-structures and its invariants reduces largely to the search for restricting geometric objects. In the latter process, an important role is played by differential criteria for restrictions, formulated in terms of structure differential forms of fibre spaces forming the base of the method of restrictions and prolongations.
References
| [1] | G.F. Laptev, "Differential geometry of imbedded manifolds. Group-theoretical method of differential-geometric investigation" Trudy Moskov. Mat. Obshch. , 2 (1953) pp. 275–382 (In Russian) |
| [2] | G.F. Laptev, , Proc. 3-rd All-Union Mat. Congress (Moscow, 1956) , 3 , Moscow (1958) pp. 409–418 |
Comments
References
| [a1] | G. Jensen, "Higher order contact of submanifolds of homogeneous spaces" , Lect. notes in math. , 610 , Springer (1977) |
| [a2] | S. Kobayashi, K. Nomizu, "Foundations of differential geometry" , 1–2 , Interscience (1979) |
Method of extensions and restrictions. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Method_of_extensions_and_restrictions&oldid=47826