Namespaces
Variants
Actions

Difference between revisions of "User:Maximilian Janisch/latexlist/latex/NoNroff/77"

From Encyclopedia of Mathematics
Jump to: navigation, search
 
(3 intermediate revisions by 2 users not shown)
Line 1: Line 1:
 
== List ==
 
== List ==
−
1. https://www.encyclopediaofmath.org/legacyimages/c/c130/c130110/c13011012.png ; $f ^ { \circ } ( x ; v ) : = \operatorname { liminf } _ { y \rightarrow x , t \downarrow 0 }  \frac { f ( y + t v ) - f ( y ) } { t }$ ; confidence 0.055
+
1. https://www.encyclopediaofmath.org/legacyimages/c/c130/c130110/c13011012.png ; $f ^ { \circ } ( x ; v ) : = \liminf _ { y \rightarrow x , t \downarrow 0 }  \frac { f ( y + t v ) - f ( y ) } { t }$ ; confidence 0.055
  
−
2. https://www.encyclopediaofmath.org/legacyimages/a/a120/a120160/a120160110.png ; $y _ { i } = e ^ { i z } \prod _ { j = 1 } ^ { p _ { t } } x _ { i j } ^ { b j } \prod _ { j ^ { \prime } = p _ { t + 1 } } ^ { p } ( 1 + x _ { i j ^ { \prime } } ) ^ { b j ^ { \prime } } e ^ { \mu i },$ ; confidence 0.054
+
2. https://www.encyclopediaofmath.org/legacyimages/a/a120/a120160/a120160110.png ; $y _ { i } = e ^ { a} \prod _ { j = 1 } ^ { p _ { t } } x _ { i j } ^ { b j } \prod _ { j ^ { \prime } = p _ { t + 1 } } ^ { p } ( 1 + x _ { i j ^ { \prime } } ) ^ { b j ^ { \prime } } e ^ { \mu i },$ ; confidence 0.054
  
 
3. https://www.encyclopediaofmath.org/legacyimages/b/b120/b120210/b12021090.png ; $\sigma _ { \alpha }$ ; confidence 0.054
 
3. https://www.encyclopediaofmath.org/legacyimages/b/b120/b120210/b12021090.png ; $\sigma _ { \alpha }$ ; confidence 0.054
  
−
4. https://www.encyclopediaofmath.org/legacyimages/c/c120/c120300/c12030095.png ; $\omega \{ K _ { i } \} ( S _ { i_1 } \ldots S _ { i_r } S _ { j S } ^ { * } \ldots S _ { j 1 } ^ { * } ) = \prod _ { k = 1 } ^ { r } \{ S _ { j _ { h } } , K _ { h } S _ { i_h } \} \delta _ { r , s }.$ ; confidence 0.054
+
4. https://www.encyclopediaofmath.org/legacyimages/c/c120/c120300/c12030095.png ; $\omega \{ K _ { i } \} ( S _ { i_1 } \ldots S _ { i_r } S _ { j_{s} } ^ { * } \ldots S _ { j_{ 1} } ^ { * } ) = \prod _ { h = 1 } ^ { r } \{ S _ { j _ { h } } , K _ { h } S _ { i_h } \} \delta _ { r , s }.$ ; confidence 0.054
  
 
5. https://www.encyclopediaofmath.org/legacyimages/s/s120/s120280/s12028042.png ; $| r g _ { 1 } | = [ g_{2} ]$ ; confidence 0.053
 
5. https://www.encyclopediaofmath.org/legacyimages/s/s120/s120280/s12028042.png ; $| r g _ { 1 } | = [ g_{2} ]$ ; confidence 0.053
  
−
6. https://www.encyclopediaofmath.org/legacyimages/b/b120/b120050/b12005061.png ; $\mathcal{M} ( \mathcal{H} _ { b } ( \mathfrak { c } _ { 0 } ) ) = \{ \tilde { \delta _ { z } } : z \in l _ { \infty } \}$ ; confidence 0.053
+
6. https://www.encyclopediaofmath.org/legacyimages/b/b120/b120050/b12005061.png ; $\mathcal{M} ( \mathcal{H} _ { b } ( c _ { 0 } ) ) = \{ \widetilde { \delta _ { z } } : z \in \operatorname{l} _ { \infty } \}$ ; confidence 0.053
  
 
7. https://www.encyclopediaofmath.org/legacyimages/g/g120/g120040/g12004080.png ; $S _ { 1,0 } ^ { m }$ ; confidence 0.053
 
7. https://www.encyclopediaofmath.org/legacyimages/g/g120/g120040/g12004080.png ; $S _ { 1,0 } ^ { m }$ ; confidence 0.053
Line 18: Line 18:
 
9. https://www.encyclopediaofmath.org/legacyimages/c/c120/c120040/c12004058.png ; $\phi _ { k } = \frac { 1 } { \langle \rho ^ { \prime } , \zeta \rangle ^ { n } } \left\langle \frac { \rho ^ { \prime } ( \zeta ) } { \langle \rho ^ { \prime } ( \zeta ) , \zeta \rangle } , z \right\rangle ^ { k } \sigma,$ ; confidence 0.053
 
9. https://www.encyclopediaofmath.org/legacyimages/c/c120/c120040/c12004058.png ; $\phi _ { k } = \frac { 1 } { \langle \rho ^ { \prime } , \zeta \rangle ^ { n } } \left\langle \frac { \rho ^ { \prime } ( \zeta ) } { \langle \rho ^ { \prime } ( \zeta ) , \zeta \rangle } , z \right\rangle ^ { k } \sigma,$ ; confidence 0.053
  
−
10. https://www.encyclopediaofmath.org/legacyimages/k/k130/k130070/k1300702.png ; $h _ { t } + h _ { X XXX } + h _ { X X } + \frac { 1 } { 2 } h _ { X } ^ { 2 } = 0,$ ; confidence 0.053
+
10. https://www.encyclopediaofmath.org/legacyimages/k/k130/k130070/k1300702.png ; $h _ { t } + h _ { xxxx } + h _ {xx } + \frac { 1 } { 2 } h _ { x } ^ { 2 } = 0,$ ; confidence 0.053
  
 
11. https://www.encyclopediaofmath.org/legacyimages/h/h130/h130070/h13007051.png ; $R _ { n - 1} : = k [ X _ { 1 } , \dots , X _ { n-1 }  ]$ ; confidence 0.053
 
11. https://www.encyclopediaofmath.org/legacyimages/h/h130/h130070/h13007051.png ; $R _ { n - 1} : = k [ X _ { 1 } , \dots , X _ { n-1 }  ]$ ; confidence 0.053
  
−
12. https://www.encyclopediaofmath.org/legacyimages/p/p130/p130070/p13007040.png ; $\left\{ \begin{array} { c } { M ( u ) = \phi \quad \text { on } D , } \\ { u |_{ \partial D = f.} } \end{array} \right.$ ; confidence 0.053
+
12. https://www.encyclopediaofmath.org/legacyimages/p/p130/p130070/p13007040.png ; $\left\{ \begin{array} { c } { M ( u ) = \phi } & {\text { on } D , } \\ { u |_{ \partial D = f.} } \end{array} \right.$ ; confidence 0.053
  
−
13. https://www.encyclopediaofmath.org/legacyimages/b/b120/b120130/b12013061.png ; $L _ { \alpha } ^ { q }$ ; confidence 0.052
+
13. https://www.encyclopediaofmath.org/legacyimages/b/b120/b120130/b12013061.png ; $L _ { a } ^ { q }$ ; confidence 0.052
  
−
14. https://www.encyclopediaofmath.org/legacyimages/c/c120/c120180/c120180493.png ; $+ 2 r d t \otimes d t + t d t \otimes d r + t d r \otimes d t$ ; confidence 0.052
+
14. https://www.encyclopediaofmath.org/legacyimages/c/c120/c120180/c120180493.png ; $+ 2 r d t \bigotimes d t + t d t \bigotimes d r + t d r \bigotimes d t$ ; confidence 0.052
  
 
15. https://www.encyclopediaofmath.org/legacyimages/a/a130/a130050/a130050148.png ; $= 1 + \sum | p _ { 1 } | ^ { - r _ { 1 } z } \ldots | p _ {m } | ^ { - r _ { m } z } =$ ; confidence 0.052
 
15. https://www.encyclopediaofmath.org/legacyimages/a/a130/a130050/a130050148.png ; $= 1 + \sum | p _ { 1 } | ^ { - r _ { 1 } z } \ldots | p _ {m } | ^ { - r _ { m } z } =$ ; confidence 0.052
Line 42: Line 42:
 
21. https://www.encyclopediaofmath.org/legacyimages/s/s120/s120200/s12020069.png ; $S ^ { \lambda } = \operatorname { span } \{ e _ { t } : t a  \lambda \square \text { tableau } \}$ ; confidence 0.051
 
21. https://www.encyclopediaofmath.org/legacyimages/s/s120/s120200/s12020069.png ; $S ^ { \lambda } = \operatorname { span } \{ e _ { t } : t a  \lambda \square \text { tableau } \}$ ; confidence 0.051
  
−
22. https://www.encyclopediaofmath.org/legacyimages/s/s120/s120200/s120200104.png ; $G L _ { n }$ ; confidence 0.051
+
22. https://www.encyclopediaofmath.org/legacyimages/s/s120/s120200/s120200104.png ; $\operatorname { GL} _ { n }$ ; confidence 0.051
  
−
23. https://www.encyclopediaofmath.org/legacyimages/m/m130/m130260/m13026072.png ; $\tilde { A } _ { s \alpha }$ ; confidence 0.051
+
23. https://www.encyclopediaofmath.org/legacyimages/m/m130/m130260/m13026072.png ; $\widetilde { A } _ { s a }$ ; confidence 0.051
  
−
24. https://www.encyclopediaofmath.org/legacyimages/e/e130/e130030/e13003033.png ; $\mathcal{C} _ { \infty } ( \Gamma \backslash G ( \mathbf{R} ) \otimes M _ { C } ) \not \subset L ^ { 2 } ( \Gamma \backslash G ( \mathbf{R} ) \otimes M _ { C } )$ ; confidence 0.051
+
24. https://www.encyclopediaofmath.org/legacyimages/e/e130/e130030/e13003033.png ; $\mathcal{C} _ { \infty } ( \Gamma \backslash G ( \mathbf{R} ) \otimes \mathcal{M} _ { \mathbf{C} } ) \not \subset L ^ { 2 } ( \Gamma \backslash G ( \mathbf{R} ) \otimes \mathcal{M} _ { \mathbf{C} } )$ ; confidence 0.051
  
 
25. https://www.encyclopediaofmath.org/legacyimages/b/b130/b130220/b130220106.png ; $Q_m u$ ; confidence 0.051
 
25. https://www.encyclopediaofmath.org/legacyimages/b/b130/b130220/b130220106.png ; $Q_m u$ ; confidence 0.051
Line 52: Line 52:
 
26. https://www.encyclopediaofmath.org/legacyimages/r/r130/r130040/r13004036.png ; $u^*$ ; confidence 0.051
 
26. https://www.encyclopediaofmath.org/legacyimages/r/r130/r130040/r13004036.png ; $u^*$ ; confidence 0.051
  
−
27. https://www.encyclopediaofmath.org/legacyimages/a/a130/a130240/a130240278.png ; $P ( \hat { \psi } - S \hat { \sigma } _ { \hat { \psi } } \leq \psi \leq \hat { \psi } + S \hat { \sigma } _ { \hat { \psi } } , \forall \psi \in L ) = 1 - \alpha,$ ; confidence 0.051
+
27. https://www.encyclopediaofmath.org/legacyimages/a/a130/a130240/a130240278.png ; $\mathsf{P} ( \widehat { \psi } - S \widehat { \sigma } _ { \widehat { \psi } } \leq \psi \leq \widehat { \psi } + S \widehat { \sigma } _ { \widehat { \psi } } , \forall \psi \in L ) = 1 - \alpha,$ ; confidence 0.051
  
 
28. https://www.encyclopediaofmath.org/legacyimages/s/s120/s120160/s1201607.png ; $I _ { d }$ ; confidence 0.051
 
28. https://www.encyclopediaofmath.org/legacyimages/s/s120/s120160/s1201607.png ; $I _ { d }$ ; confidence 0.051
Line 58: Line 58:
 
29. https://www.encyclopediaofmath.org/legacyimages/b/b120/b120320/b12032091.png ; $\frac { k } { k + 1 } \frac { \operatorname { log } a _ { \mathfrak { m } } } { \operatorname { log } m } \leq \frac { \operatorname { log } a _ { \mathfrak { n } } } { \operatorname { log } n } \leq \frac { k + 1 } { k } \frac { \operatorname { log } a _ { \mathfrak { m } } } { \operatorname { log } m }.$ ; confidence 0.050
 
29. https://www.encyclopediaofmath.org/legacyimages/b/b120/b120320/b12032091.png ; $\frac { k } { k + 1 } \frac { \operatorname { log } a _ { \mathfrak { m } } } { \operatorname { log } m } \leq \frac { \operatorname { log } a _ { \mathfrak { n } } } { \operatorname { log } n } \leq \frac { k + 1 } { k } \frac { \operatorname { log } a _ { \mathfrak { m } } } { \operatorname { log } m }.$ ; confidence 0.050
  
−
30. https://www.encyclopediaofmath.org/legacyimages/a/a120/a120080/a1200801.png ; $\begin{cases}  { \frac { \partial ^ { 2 } u } { \partial t ^ { 2 } } = \sum _ { i , j = 1 } ^ { m } \frac { \partial } { \partial x _ { i } } \{ \alpha _ { j } , ( x ) \frac { \partial u } { \partial x _ { j } } \} + c ( x ) u + f ( x , t ) },
+
30. https://www.encyclopediaofmath.org/legacyimages/a/a120/a120080/a1200801.png ; $\begin{cases}  { \frac { \partial ^ { 2 } u } { \partial t ^ { 2 } } = \sum _ { i , j = 1 } ^ { m } \frac { \partial } { \partial x _ { i } } \left\{ a _ {i, j } ( x ) \frac { \partial u } { \partial x _ { j } } \right\} + c ( x ) u + f ( x , t ) },
 
\\{ ( x , t ) \in \Omega \times [ 0 , T ] },
 
\\{ ( x , t ) \in \Omega \times [ 0 , T ] },
 
\\{ u ( x , 0 ) = u _ { 0 } ( x ) , \frac { \partial u } { \partial t } ( x , 0 ) = u _ { 1 } ( x ) , x \in \Omega } ,\end{cases}$ ; confidence 0.050
 
\\{ u ( x , 0 ) = u _ { 0 } ( x ) , \frac { \partial u } { \partial t } ( x , 0 ) = u _ { 1 } ( x ) , x \in \Omega } ,\end{cases}$ ; confidence 0.050
  
−
31. https://www.encyclopediaofmath.org/legacyimages/l/l057/l057020/l05702010.png ; $F _ { R } + 1 \rightarrow F _ { N } + 1 / l ^ { n } F _ { N } + 1$ ; confidence 0.050
+
31. https://www.encyclopediaofmath.org/legacyimages/l/l057/l057020/l05702010.png ; $F _ { n+1 }  \rightarrow F _ { n+1 } / l ^ { n } F _ { n+1 } $ ; confidence 0.050
  
−
32. https://www.encyclopediaofmath.org/legacyimages/b/b130/b130060/b13006011.png ; $\| A \| = \operatorname { max } _ { x \neq 0 } \| A x \| / \| x \| = \operatorname { max } _ { | x | } \| = 1 \| A x \|$ ; confidence 0.050
+
32. https://www.encyclopediaofmath.org/legacyimages/b/b130/b130060/b13006011.png ; $\| A \| = \operatorname { max } _ { x \neq 0 } \| A x \| / \| x \| = \operatorname { max } _ { \| x \| =1 }  \| A x \|$ ; confidence 0.050
  
−
33. https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009061.png ; $\Gamma / \Gamma ^ { p m } \rightarrow \Gamma / \Gamma ^ { p , R }$ ; confidence 0.050
+
33. https://www.encyclopediaofmath.org/legacyimages/i/i130/i130090/i13009061.png ; $\Gamma / \Gamma ^ { p^m } \rightarrow \Gamma / \Gamma ^ { p ^n }$ ; confidence 0.050

Latest revision as of 12:04, 11 May 2020

List

1. 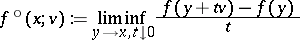c13011012.png ; $f ^ { \circ } ( x ; v ) : = \liminf _ { y \rightarrow x , t \downarrow 0 } \frac { f ( y + t v ) - f ( y ) } { t }$ ; confidence 0.055

2. 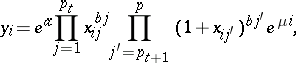a120160110.png ; $y _ { i } = e ^ { a} \prod _ { j = 1 } ^ { p _ { t } } x _ { i j } ^ { b j } \prod _ { j ^ { \prime } = p _ { t + 1 } } ^ { p } ( 1 + x _ { i j ^ { \prime } } ) ^ { b j ^ { \prime } } e ^ { \mu i },$ ; confidence 0.054

3. 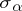b12021090.png ; $\sigma _ { \alpha }$ ; confidence 0.054

4. 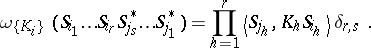c12030095.png ; $\omega \{ K _ { i } \} ( S _ { i_1 } \ldots S _ { i_r } S _ { j_{s} } ^ { * } \ldots S _ { j_{ 1} } ^ { * } ) = \prod _ { h = 1 } ^ { r } \{ S _ { j _ { h } } , K _ { h } S _ { i_h } \} \delta _ { r , s }.$ ; confidence 0.054

5. 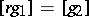s12028042.png ; $| r g _ { 1 } | = [ g_{2} ]$ ; confidence 0.053

6. 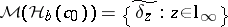b12005061.png ; $\mathcal{M} ( \mathcal{H} _ { b } ( c _ { 0 } ) ) = \{ \widetilde { \delta _ { z } } : z \in \operatorname{l} _ { \infty } \}$ ; confidence 0.053

7. 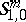g12004080.png ; $S _ { 1,0 } ^ { m }$ ; confidence 0.053

8. b13006010.png ; $\|AB \| \leq \| A \| \| B \|$ ; Picture is maybe incomplete?

9. 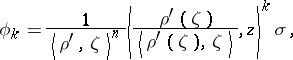c12004058.png ; $\phi _ { k } = \frac { 1 } { \langle \rho ^ { \prime } , \zeta \rangle ^ { n } } \left\langle \frac { \rho ^ { \prime } ( \zeta ) } { \langle \rho ^ { \prime } ( \zeta ) , \zeta \rangle } , z \right\rangle ^ { k } \sigma,$ ; confidence 0.053

10. k1300702.png ; $h _ { t } + h _ { xxxx } + h _ {xx } + \frac { 1 } { 2 } h _ { x } ^ { 2 } = 0,$ ; confidence 0.053

11. 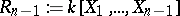h13007051.png ; $R _ { n - 1} : = k [ X _ { 1 } , \dots , X _ { n-1 } ]$ ; confidence 0.053

12. p13007040.png ; $\left\{ \begin{array} { c } { M ( u ) = \phi } & {\text { on } D , } \\ { u |_{ \partial D = f.} } \end{array} \right.$ ; confidence 0.053

13. 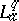b12013061.png ; $L _ { a } ^ { q }$ ; confidence 0.052

14. 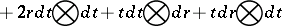c120180493.png ; $+ 2 r d t \bigotimes d t + t d t \bigotimes d r + t d r \bigotimes d t$ ; confidence 0.052

15. 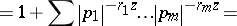a130050148.png ; $= 1 + \sum | p _ { 1 } | ^ { - r _ { 1 } z } \ldots | p _ {m } | ^ { - r _ { m } z } =$ ; confidence 0.052

16. 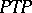v09690036.png ; $PTP$ ; confidence 0.052

17. 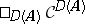y120010110.png ; $\square _ { D(A) } \mathcal{C}^{D ( A )}$ ; confidence 0.052

18. 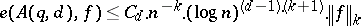s12016031.png ; $e ( A ( q , d ) , f ) \leq C _ { d }. n ^ { - k } .( \operatorname { log } n ) ^ { ( d - 1 ) . ( k + 1 ) }. \| f \| _ { k }$ ; confidence 0.052

19. 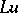a01293016.png ; $Lu$ ; confidence 0.051

20. 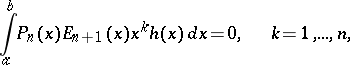s1202502.png ; $\int _ { a } ^ { b } P _ { n } ( x ) E _ { n + 1 } ( x ) x ^ { k } h ( x ) d x = 0 , \quad k = 1 , \dots , n,$ ; confidence 0.051

21. 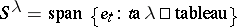s12020069.png ; $S ^ { \lambda } = \operatorname { span } \{ e _ { t } : t a \lambda \square \text { tableau } \}$ ; confidence 0.051

22. 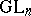s120200104.png ; $\operatorname { GL} _ { n }$ ; confidence 0.051

23. 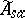m13026072.png ; $\widetilde { A } _ { s a }$ ; confidence 0.051

24. 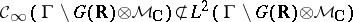e13003033.png ; $\mathcal{C} _ { \infty } ( \Gamma \backslash G ( \mathbf{R} ) \otimes \mathcal{M} _ { \mathbf{C} } ) \not \subset L ^ { 2 } ( \Gamma \backslash G ( \mathbf{R} ) \otimes \mathcal{M} _ { \mathbf{C} } )$ ; confidence 0.051

25. 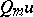b130220106.png ; $Q_m u$ ; confidence 0.051

26. 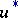r13004036.png ; $u^*$ ; confidence 0.051

27. 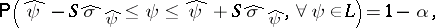a130240278.png ; $\mathsf{P} ( \widehat { \psi } - S \widehat { \sigma } _ { \widehat { \psi } } \leq \psi \leq \widehat { \psi } + S \widehat { \sigma } _ { \widehat { \psi } } , \forall \psi \in L ) = 1 - \alpha,$ ; confidence 0.051

28. s1201607.png ; $I _ { d }$ ; confidence 0.051

29. 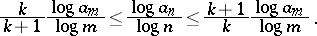b12032091.png ; $\frac { k } { k + 1 } \frac { \operatorname { log } a _ { \mathfrak { m } } } { \operatorname { log } m } \leq \frac { \operatorname { log } a _ { \mathfrak { n } } } { \operatorname { log } n } \leq \frac { k + 1 } { k } \frac { \operatorname { log } a _ { \mathfrak { m } } } { \operatorname { log } m }.$ ; confidence 0.050

30. 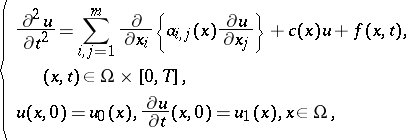a1200801.png ; $\begin{cases} { \frac { \partial ^ { 2 } u } { \partial t ^ { 2 } } = \sum _ { i , j = 1 } ^ { m } \frac { \partial } { \partial x _ { i } } \left\{ a _ {i, j } ( x ) \frac { \partial u } { \partial x _ { j } } \right\} + c ( x ) u + f ( x , t ) }, \\{ ( x , t ) \in \Omega \times [ 0 , T ] }, \\{ u ( x , 0 ) = u _ { 0 } ( x ) , \frac { \partial u } { \partial t } ( x , 0 ) = u _ { 1 } ( x ) , x \in \Omega } ,\end{cases}$ ; confidence 0.050

31. 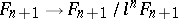l05702010.png ; $F _ { n+1 } \rightarrow F _ { n+1 } / l ^ { n } F _ { n+1 } $ ; confidence 0.050

32. 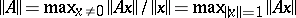b13006011.png ; $\| A \| = \operatorname { max } _ { x \neq 0 } \| A x \| / \| x \| = \operatorname { max } _ { \| x \| =1 } \| A x \|$ ; confidence 0.050

33. 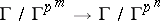i13009061.png ; $\Gamma / \Gamma ^ { p^m } \rightarrow \Gamma / \Gamma ^ { p ^n }$ ; confidence 0.050

How to Cite This Entry:
Maximilian Janisch/latexlist/latex/NoNroff/77. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Maximilian_Janisch/latexlist/latex/NoNroff/77&oldid=45646
Retrieved from "https://encyclopediaofmath.org/index.php?title=User:Maximilian_Janisch/latexlist/latex/NoNroff/77&oldid=45872"