Difference between revisions of "User:Maximilian Janisch/Sandbox"
(AUTOMATIC EDIT (Latexlist): Replaced 18.2% images by TEX code) |
(test) |
||
| (8 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | {{TEX|partial}} | + | {{TEX|partial}}<div class="Vorlage_Achtung" style="border: 0.18em solid #FF6666; border-left:1em solid #FF6666; margin:0.5em 0em; overflow:hidden; padding:0.5em; text-align: left;"> |
| + | This page is a copy of the article [[Bayesian approach]] in order to test [[User:Maximilian_Janisch/latexlist|automatic LaTeXification]]. This article is not my work. | ||
| + | </div> | ||
| + | Test | ||
| + | ''to statistical problems'' | ||
| − | + | An approach based on the assumption that to any parameter in a statistical problem there can be assigned a definite probability distribution. Any general statistical decision problem is determined by the following elements: by a space $( X , B X )$ of (potential) samples $\pi$, by a space $( \Theta , B _ { \Theta } )$ of values of the unknown parameter $6$, by a family of probability distributions $\{ P _ { \theta } : \theta \in \Theta \}$ on $( X , B X )$, by a space of decisions $( D , B _ { D } )$ and by a function $L ( \theta , d )$, which characterizes the losses caused by accepting the decision $a$ when the true value of the parameter is $6$. The objective of decision making is to find in a certain sense an optimal rule (decision function) $\delta = \delta ( x )$, assigning to each result of an observation $X \in X$ the decision $\delta ( x ) \in D$. In the Bayesian approach, when it is assumed that the unknown parameter $6$ is a random variable with a given (a priori) distribution $\pi = \pi ( d \theta )$ on $( \Theta , B _ { \Theta } )$ the best decision function ([[Bayesian decision function|Bayesian decision function]]) $\delta ^ { * } = \delta ^ { * } ( x )$ is defined as the function for which the minimum expected loss $\delta \rho ( \pi , \delta )$, where | |
| − | \begin{equation} | + | \begin{equation} \rho ( \pi , \delta ) = \int _ { \Theta } \rho ( \theta , \delta ) \pi ( d \theta ) \end{equation} |
| − | + | and | |
| − | \begin{equation} \ | + | \begin{equation} \rho ( \theta , \delta ) = \int _ { Y } L ( \theta , \delta ( x ) ) P _ { \theta } ( d x ) \end{equation} |
| − | + | is attained. Thus, | |
| − | + | \begin{equation} \rho ( \pi , \delta ^ { * } ) = \operatorname { inf } _ { \delta } \int _ { \Theta } \int _ { X } L ( \theta , \delta ( x ) ) P _ { \theta } ( d x ) \pi ( d \theta ) \end{equation} | |
| − | + | In searching for the Bayesian decision function $\delta ^ { * } = \delta ^ { * } ( x )$, the following remark is useful. Let $P _ { \theta } ( d x ) = p ( x | \theta ) d \mu ( x )$, $\pi ( d \theta ) = \pi ( \theta ) d \nu ( \theta )$, where $\mu$ and $2$ are certain $\Omega$-finite measures. One then finds, assuming that the order of integration may be changed, | |
| − | + | \begin{equation} \int \int _ { \Theta } L ( \theta , \delta ( x ) ) P _ { \theta } ( d x ) \pi ( d \theta ) = \end{equation} | |
| − | + | \begin{equation} = \int \int _ { \Theta } L ( \theta , \delta ( x ) ) p ( x | \theta ) \pi ( \theta ) d \mu ( x ) d \nu ( \theta ) = \end{equation} | |
| − | + | \begin{equation} = \int _ { X } d \mu ( x ) [ \int _ { \Theta } L ( \theta , \delta ( x ) ) p ( x | \theta ) \pi ( \theta ) d \nu ( \theta ) ] \end{equation} | |
| − | \ | + | It is seen from the above that for a given $x \in X , \delta ^ { * } ( x )$ is that value of $d ^ { x }$ for which |
| − | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015390/b01539033.png"/></td> </tr></table> | |
| − | + | is attained, or, what is equivalent, for which | |
| − | ( | + | \begin{equation} \operatorname { inf } _ { d } \int _ { \Theta } L ( \theta , d ) \frac { p ( x | \theta ) \pi ( \theta ) } { p ( x ) } d \nu ( \theta ) \end{equation} |
| − | + | is attained, where | |
| − | + | \begin{equation} p ( x ) = \int _ { \Theta } p ( x | \theta ) \pi ( \theta ) d \nu ( \theta ) \end{equation} | |
| − | + | But, according to the [[Bayes formula|Bayes formula]] | |
| − | + | \begin{equation} \int _ { \Theta } L ( \theta , d ) \frac { p ( x | \theta ) \pi ( \theta ) } { p ( x ) } d \nu ( \theta ) = E [ L ( \theta , d ) | x ] \end{equation} | |
| − | + | Thus, for a given $\pi$, $\delta ^ { * } ( x )$ is that value of $d ^ { x }$ for which the conditional average loss $E [ L ( \theta , d ) | x ]$ attains a minimum. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Example. (The Bayesian approach applied to the case of distinguishing between two simple hypotheses.) Let $= \{ \theta _ { 1 } , \theta _ { 2 } \}$, $D = \{ d _ { 1 } , d _ { 2 } \}$, $L _ { i j } = L = ( \theta _ { i } , d _ { j } )$, $i , j = 1,2$; $\pi ( \theta _ { 1 } ) = \pi _ { 1 }$, $\pi ( \theta _ { 2 } ) = \pi _ { 2 }$, $\pi _ { 1 } + \pi _ { 2 } = 1$. If the solution $a$ is identified with the acceptance of the hypothesis $H _ { \hat { j } }$: $\theta = \theta _ { i }$, it is natural to assume that $L _ { 11 } < L _ { 12 }$, $L _ { 22 } < L _ { 21 }$. Then | |
| − | + | \begin{equation} \rho ( \pi , \delta ) = \int _ { X } [ \pi _ { 1 } p ( x | \theta _ { 1 } ) L ( \theta _ { 1 } , \delta ( x ) ) + \end{equation} | |
| − | + | \begin{equation} + \pi _ { 2 } p ( x | \theta _ { 2 } ) L ( \theta _ { 2 } , \delta ( x ) ) ] d \mu ( x ) \end{equation} | |
| − | + | implies that $\delta \rho ( \pi , \delta )$ is attained for the function | |
| − | + | \begin{equation} \delta ^ { * } ( x ) = \left\{ \begin{array} { l l } { d _ { 1 } , } & { \text { if } \frac { p ( x | \theta _ { 2 } ) } { p ( x | \theta _ { 1 } ) } \leq \frac { \pi _ { 1 } } { \pi _ { 2 } } \frac { L _ { 12 } - L _ { 11 } } { L _ { 21 } - L _ { 22 } } } \\ { d _ { 2 } , } & { \text { if } \frac { p ( x | \theta _ { 2 } ) } { p ( x | \theta _ { 1 } ) } \geq \frac { \pi _ { 1 } } { \pi _ { 2 } } \frac { L _ { 12 } - L _ { 11 } } { L _ { 21 } - L _ { 22 } } } \end{array} \right. \end{equation} | |
| − | + | The advantage of the Bayesian approach consists in the fact that, unlike the losses $\rho ( \theta , \delta )$, the expected losses $\rho ( \pi , \delta )$ are numbers which are dependent on the unknown parameter $6$, and, consequently, it is known that solutions $\delta _ { \epsilon } ^ { * }$ for which | |
| − | + | \begin{equation} \rho ( \pi , \delta _ { \epsilon } ^ { * } ) \leq \operatorname { inf } _ { \delta } \rho ( \pi , \delta ) + \epsilon \end{equation} | |
| − | + | and which are, if not optimal, at least <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015390/b01539062.png"/>-optimal $( \epsilon > 0 )$, are certain to exist. The disadvantage of the Bayesian approach is the necessity of postulating both the existence of an a priori distribution of the unknown parameter and its precise form (the latter disadvantage may be overcome to a certain extent by adopting an empirical Bayesian approach, cf. [[Bayesian approach, empirical|Bayesian approach, empirical]]). | |
====References==== | ====References==== | ||
| − | <table>< | + | <table><tr><td valign="top">[1]</td> <td valign="top"> A. Wald, "Statistical decision functions" , Wiley (1950)</td></tr><tr><td valign="top">[2]</td> <td valign="top"> M.H. de Groot, "Optimal statistical decisions" , McGraw-Hill (1970)</td></tr></table> |
Latest revision as of 13:45, 17 October 2019
Test to statistical problems
An approach based on the assumption that to any parameter in a statistical problem there can be assigned a definite probability distribution. Any general statistical decision problem is determined by the following elements: by a space $( X , B X )$ of (potential) samples $\pi$, by a space $( \Theta , B _ { \Theta } )$ of values of the unknown parameter $6$, by a family of probability distributions $\{ P _ { \theta } : \theta \in \Theta \}$ on $( X , B X )$, by a space of decisions $( D , B _ { D } )$ and by a function $L ( \theta , d )$, which characterizes the losses caused by accepting the decision $a$ when the true value of the parameter is $6$. The objective of decision making is to find in a certain sense an optimal rule (decision function) $\delta = \delta ( x )$, assigning to each result of an observation $X \in X$ the decision $\delta ( x ) \in D$. In the Bayesian approach, when it is assumed that the unknown parameter $6$ is a random variable with a given (a priori) distribution $\pi = \pi ( d \theta )$ on $( \Theta , B _ { \Theta } )$ the best decision function (Bayesian decision function) $\delta ^ { * } = \delta ^ { * } ( x )$ is defined as the function for which the minimum expected loss $\delta \rho ( \pi , \delta )$, where
\begin{equation} \rho ( \pi , \delta ) = \int _ { \Theta } \rho ( \theta , \delta ) \pi ( d \theta ) \end{equation}
and
\begin{equation} \rho ( \theta , \delta ) = \int _ { Y } L ( \theta , \delta ( x ) ) P _ { \theta } ( d x ) \end{equation}
is attained. Thus,
\begin{equation} \rho ( \pi , \delta ^ { * } ) = \operatorname { inf } _ { \delta } \int _ { \Theta } \int _ { X } L ( \theta , \delta ( x ) ) P _ { \theta } ( d x ) \pi ( d \theta ) \end{equation}
In searching for the Bayesian decision function $\delta ^ { * } = \delta ^ { * } ( x )$, the following remark is useful. Let $P _ { \theta } ( d x ) = p ( x | \theta ) d \mu ( x )$, $\pi ( d \theta ) = \pi ( \theta ) d \nu ( \theta )$, where $\mu$ and $2$ are certain $\Omega$-finite measures. One then finds, assuming that the order of integration may be changed,
\begin{equation} \int \int _ { \Theta } L ( \theta , \delta ( x ) ) P _ { \theta } ( d x ) \pi ( d \theta ) = \end{equation}
\begin{equation} = \int \int _ { \Theta } L ( \theta , \delta ( x ) ) p ( x | \theta ) \pi ( \theta ) d \mu ( x ) d \nu ( \theta ) = \end{equation}
\begin{equation} = \int _ { X } d \mu ( x ) [ \int _ { \Theta } L ( \theta , \delta ( x ) ) p ( x | \theta ) \pi ( \theta ) d \nu ( \theta ) ] \end{equation}
It is seen from the above that for a given $x \in X , \delta ^ { * } ( x )$ is that value of $d ^ { x }$ for which
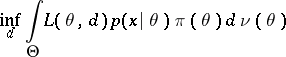 |
is attained, or, what is equivalent, for which
\begin{equation} \operatorname { inf } _ { d } \int _ { \Theta } L ( \theta , d ) \frac { p ( x | \theta ) \pi ( \theta ) } { p ( x ) } d \nu ( \theta ) \end{equation}
is attained, where
\begin{equation} p ( x ) = \int _ { \Theta } p ( x | \theta ) \pi ( \theta ) d \nu ( \theta ) \end{equation}
But, according to the Bayes formula
\begin{equation} \int _ { \Theta } L ( \theta , d ) \frac { p ( x | \theta ) \pi ( \theta ) } { p ( x ) } d \nu ( \theta ) = E [ L ( \theta , d ) | x ] \end{equation}
Thus, for a given $\pi$, $\delta ^ { * } ( x )$ is that value of $d ^ { x }$ for which the conditional average loss $E [ L ( \theta , d ) | x ]$ attains a minimum.
Example. (The Bayesian approach applied to the case of distinguishing between two simple hypotheses.) Let $= \{ \theta _ { 1 } , \theta _ { 2 } \}$, $D = \{ d _ { 1 } , d _ { 2 } \}$, $L _ { i j } = L = ( \theta _ { i } , d _ { j } )$, $i , j = 1,2$; $\pi ( \theta _ { 1 } ) = \pi _ { 1 }$, $\pi ( \theta _ { 2 } ) = \pi _ { 2 }$, $\pi _ { 1 } + \pi _ { 2 } = 1$. If the solution $a$ is identified with the acceptance of the hypothesis $H _ { \hat { j } }$: $\theta = \theta _ { i }$, it is natural to assume that $L _ { 11 } < L _ { 12 }$, $L _ { 22 } < L _ { 21 }$. Then
\begin{equation} \rho ( \pi , \delta ) = \int _ { X } [ \pi _ { 1 } p ( x | \theta _ { 1 } ) L ( \theta _ { 1 } , \delta ( x ) ) + \end{equation}
\begin{equation} + \pi _ { 2 } p ( x | \theta _ { 2 } ) L ( \theta _ { 2 } , \delta ( x ) ) ] d \mu ( x ) \end{equation}
implies that $\delta \rho ( \pi , \delta )$ is attained for the function
\begin{equation} \delta ^ { * } ( x ) = \left\{ \begin{array} { l l } { d _ { 1 } , } & { \text { if } \frac { p ( x | \theta _ { 2 } ) } { p ( x | \theta _ { 1 } ) } \leq \frac { \pi _ { 1 } } { \pi _ { 2 } } \frac { L _ { 12 } - L _ { 11 } } { L _ { 21 } - L _ { 22 } } } \\ { d _ { 2 } , } & { \text { if } \frac { p ( x | \theta _ { 2 } ) } { p ( x | \theta _ { 1 } ) } \geq \frac { \pi _ { 1 } } { \pi _ { 2 } } \frac { L _ { 12 } - L _ { 11 } } { L _ { 21 } - L _ { 22 } } } \end{array} \right. \end{equation}
The advantage of the Bayesian approach consists in the fact that, unlike the losses $\rho ( \theta , \delta )$, the expected losses $\rho ( \pi , \delta )$ are numbers which are dependent on the unknown parameter $6$, and, consequently, it is known that solutions $\delta _ { \epsilon } ^ { * }$ for which
\begin{equation} \rho ( \pi , \delta _ { \epsilon } ^ { * } ) \leq \operatorname { inf } _ { \delta } \rho ( \pi , \delta ) + \epsilon \end{equation}
and which are, if not optimal, at least  -optimal $( \epsilon > 0 )$, are certain to exist. The disadvantage of the Bayesian approach is the necessity of postulating both the existence of an a priori distribution of the unknown parameter and its precise form (the latter disadvantage may be overcome to a certain extent by adopting an empirical Bayesian approach, cf. Bayesian approach, empirical).
-optimal $( \epsilon > 0 )$, are certain to exist. The disadvantage of the Bayesian approach is the necessity of postulating both the existence of an a priori distribution of the unknown parameter and its precise form (the latter disadvantage may be overcome to a certain extent by adopting an empirical Bayesian approach, cf. Bayesian approach, empirical).
References
| [1] | A. Wald, "Statistical decision functions" , Wiley (1950) |
| [2] | M.H. de Groot, "Optimal statistical decisions" , McGraw-Hill (1970) |
Maximilian Janisch/Sandbox. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Maximilian_Janisch/Sandbox&oldid=43662