Difference between revisions of "User:Maximilian Janisch/latexlist"
(AUTOMATIC EDIT: Updated image/latex database (currently 125 images indexed; order by confidence, reverse: True.) |
(AUTOMATIC EDIT: Updated image/latex database (currently 200 images indexed; order by confidence, reverse: True.) |
||
| Line 3: | Line 3: | ||
== List == | == List == | ||
<img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010129.png" /> : $15$ | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010129.png" /> : $15$ | ||
| + | (confidence 1.00) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010143.png" /> : $15$ | ||
(confidence 1.00) | (confidence 1.00) | ||
| Line 12: | Line 15: | ||
<img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010151.png" /> : $4 n + 3$ | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010151.png" /> : $4 n + 3$ | ||
| + | (confidence 1.00) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010118.png" /> : $4 n + 3$ | ||
(confidence 1.00) | (confidence 1.00) | ||
| Line 18: | Line 24: | ||
<img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010115.png" /> : $11$ | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010115.png" /> : $11$ | ||
| + | (confidence 1.00) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010142.png" /> : $11$ | ||
(confidence 1.00) | (confidence 1.00) | ||
| Line 27: | Line 36: | ||
<img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010146.png" /> : $7$ | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010146.png" /> : $7$ | ||
| + | (confidence 1.00) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010141.png" /> : $7$ | ||
| + | (confidence 1.00) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010156.png" /> : $7$ | ||
(confidence 1.00) | (confidence 1.00) | ||
| Line 36: | Line 51: | ||
<img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t12001077.png" /> : $\xi ( \tau )$ | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t12001077.png" /> : $\xi ( \tau )$ | ||
| + | (confidence 1.00) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/a/a010/a010020/a01002013.png" /> : $\sigma \delta$ | ||
| + | (confidence 1.00) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010130.png" /> : $b _ { 2 } \neq b _ { 6 }$ | ||
(confidence 1.00) | (confidence 1.00) | ||
| Line 48: | Line 69: | ||
<img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t12001049.png" /> : $\{ \xi ^ { 1 } , \xi ^ { 2 } , \xi ^ { 3 } \}$ | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t12001049.png" /> : $\{ \xi ^ { 1 } , \xi ^ { 2 } , \xi ^ { 3 } \}$ | ||
| + | (confidence 1.00) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t12001053.png" /> : $\{ \xi ^ { 1 } , \xi ^ { 2 } , \xi ^ { 3 } \}$ | ||
| + | (confidence 1.00) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t12001031.png" /> : $\{ \xi ^ { 1 } , \xi ^ { 2 } , \xi ^ { 3 } \}$ | ||
| + | (confidence 1.00) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t12001037.png" /> : $\{ \xi ^ { 1 } , \xi ^ { 2 } , \xi ^ { 3 } \}$ | ||
(confidence 1.00) | (confidence 1.00) | ||
<img src ="https://www.encyclopediaofmath.org/legacyimages/a/a130/a130010/a1300105.png" /> : $A$ | <img src ="https://www.encyclopediaofmath.org/legacyimages/a/a130/a130010/a1300105.png" /> : $A$ | ||
| + | (confidence 1.00) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/a/a010/a010080/a0100804.png" /> : $A$ | ||
| + | (confidence 1.00) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/a/a010/a010080/a01008025.png" /> : $A$ | ||
| + | (confidence 1.00) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/a/a010/a010080/a01008013.png" /> : $A$ | ||
| + | (confidence 1.00) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/a/a010/a010080/a0100809.png" /> : $A$ | ||
| + | (confidence 1.00) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/a/a010/a010080/a01008014.png" /> : $A$ | ||
| + | (confidence 1.00) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/a/a010/a010080/a01008011.png" /> : $A$ | ||
| + | (confidence 1.00) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/a/a010/a010080/a01008035.png" /> : $A$ | ||
| + | (confidence 1.00) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010128.png" /> : $b _ { 2 } \neq b _ { 4 }$ | ||
(confidence 1.00) | (confidence 1.00) | ||
<img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010107.png" /> : $n \geq 0$ | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010107.png" /> : $n \geq 0$ | ||
(confidence 1.00) | (confidence 1.00) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010117.png" /> : $8$ | ||
| + | (confidence 0.99) | ||
<img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t12001058.png" /> : $F _ { 3 }$ | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t12001058.png" /> : $F _ { 3 }$ | ||
| Line 133: | Line 190: | ||
<img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010152.png" /> : $3$ | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010152.png" /> : $3$ | ||
(confidence 0.99) | (confidence 0.99) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010150.png" /> : $3$ | ||
| + | (confidence 0.99) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010157.png" /> : $3$ | ||
| + | (confidence 0.99) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010119.png" /> : $3$ | ||
| + | (confidence 0.99) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010153.png" /> : $3$ | ||
| + | (confidence 0.99) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t12001018.png" /> : $3$ | ||
| + | (confidence 0.99) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010127.png" /> : $3$ | ||
| + | (confidence 0.99) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t12001091.png" /> : $z$ | ||
| + | (confidence 0.99) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t12001083.png" /> : $z$ | ||
| + | (confidence 0.99) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t12001072.png" /> : $\xi ( \tau ) = \tau _ { 1 } \xi ^ { 1 } + \tau _ { 2 } \xi ^ { 2 } + \tau _ { 3 } \xi ^ { 3 }$ | ||
| + | (confidence 0.98) | ||
<img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010125.png" /> : $i < n$ | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010125.png" /> : $i < n$ | ||
| Line 150: | Line 234: | ||
<img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010123.png" /> : $\sum _ { k = 1 } ^ { n } k ( n + 1 - k ) ( n + 1 - 2 k ) b _ { 2 k } = 0$ | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010123.png" /> : $\sum _ { k = 1 } ^ { n } k ( n + 1 - k ) ( n + 1 - 2 k ) b _ { 2 k } = 0$ | ||
| + | (confidence 0.96) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010110.png" /> : $k > 7$ | ||
(confidence 0.96) | (confidence 0.96) | ||
| Line 186: | Line 273: | ||
<img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t12001080.png" /> : $S$ | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t12001080.png" /> : $S$ | ||
| + | (confidence 0.95) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t12001087.png" /> : $S$ | ||
| + | (confidence 0.95) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t12001030.png" /> : $S$ | ||
| + | (confidence 0.95) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t12001015.png" /> : $S$ | ||
| + | (confidence 0.95) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t12001076.png" /> : $S$ | ||
(confidence 0.95) | (confidence 0.95) | ||
| Line 201: | Line 300: | ||
<img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t12001064.png" /> : $5 ^ { 3 }$ | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t12001064.png" /> : $5 ^ { 3 }$ | ||
| + | (confidence 0.94) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t1200106.png" /> : $U ( ( m + 1 ) / 2 )$ | ||
(confidence 0.94) | (confidence 0.94) | ||
| Line 213: | Line 315: | ||
<img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t12001086.png" /> : $0$ | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t12001086.png" /> : $0$ | ||
| + | (confidence 0.93) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t12001069.png" /> : $0$ | ||
| + | (confidence 0.93) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t12001057.png" /> : $0$ | ||
(confidence 0.93) | (confidence 0.93) | ||
<img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t12001061.png" /> : $\Gamma \subset \operatorname { SU } ( 2 )$ | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t12001061.png" /> : $\Gamma \subset \operatorname { SU } ( 2 )$ | ||
| + | (confidence 0.92) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/a/a010/a010080/a01008024.png" /> : $M$ | ||
| + | (confidence 0.92) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010103.png" /> : $G$ | ||
| + | (confidence 0.92) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t12001098.png" /> : $G$ | ||
(confidence 0.92) | (confidence 0.92) | ||
| Line 225: | Line 342: | ||
<img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t12001010.png" /> : $C ( S )$ | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t12001010.png" /> : $C ( S )$ | ||
| + | (confidence 0.90) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t12001025.png" /> : $C ( S )$ | ||
(confidence 0.90) | (confidence 0.90) | ||
| Line 261: | Line 381: | ||
<img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t12001075.png" /> : $5 ^ { 2 }$ | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t12001075.png" /> : $5 ^ { 2 }$ | ||
| + | (confidence 0.80) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010104.png" /> : $\operatorname { Sp } ( n + 1 ) / \operatorname { Sp } ( n ) , \quad \operatorname { Sp } ( n + 1 ) / \operatorname { Sp } ( n ) \times Z _ { 2 }$ | ||
(confidence 0.80) | (confidence 0.80) | ||
| Line 276: | Line 399: | ||
<img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t12001099.png" /> : $\triangle ( G / K )$ | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t12001099.png" /> : $\triangle ( G / K )$ | ||
| + | (confidence 0.77) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t1200109.png" /> : $1$ | ||
(confidence 0.77) | (confidence 0.77) | ||
| Line 286: | Line 412: | ||
<img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t12001040.png" /> : $\alpha = 1,2,3$ | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t12001040.png" /> : $\alpha = 1,2,3$ | ||
(confidence 0.74) | (confidence 0.74) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t12001027.png" /> : $\alpha = 1,2,3$ | ||
| + | (confidence 0.74) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t12001095.png" /> : $\operatorname { dim } ( S ) = 4 n + 3$ | ||
| + | (confidence 0.73) | ||
<img src ="https://www.encyclopediaofmath.org/legacyimages/a/a130/a130010/a13001014.png" /> : $R e l$ | <img src ="https://www.encyclopediaofmath.org/legacyimages/a/a130/a130010/a13001014.png" /> : $R e l$ | ||
(confidence 0.69) | (confidence 0.69) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t12001026.png" /> : $\xi ^ { \alpha } = I ^ { \alpha } ( \partial _ { r } )$ | ||
| + | (confidence 0.67) | ||
<img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010138.png" /> : $p$ | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010138.png" /> : $p$ | ||
(confidence 0.64) | (confidence 0.64) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t1200107.png" /> : $m = 2 l + 1$ | ||
| + | (confidence 0.61) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010136.png" /> : $p = ( p _ { 1 } , \dots , p _ { n } + 2 )$ | ||
| + | (confidence 0.61) | ||
<img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010100.png" /> : $O = G / Sp ( 1 ) . K$ | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010100.png" /> : $O = G / Sp ( 1 ) . K$ | ||
(confidence 0.57) | (confidence 0.57) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010114.png" /> : $\operatorname { lim } ( S ) = 7$ | ||
| + | (confidence 0.53) | ||
<img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010135.png" /> : $S ( p )$ | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010135.png" /> : $S ( p )$ | ||
| Line 301: | Line 445: | ||
<img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010137.png" /> : $S ( p )$ | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010137.png" /> : $S ( p )$ | ||
(confidence 0.52) | (confidence 0.52) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/a/a010/a010080/a0100803.png" /> : $X$ | ||
| + | (confidence 0.51) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t1200104.png" /> : $m$ | ||
| + | (confidence 0.50) | ||
<img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t12001097.png" /> : $SO ( 4 n + 3 )$ | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t12001097.png" /> : $SO ( 4 n + 3 )$ | ||
| Line 307: | Line 457: | ||
<img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010120.png" /> : $b _ { 2 } ( S ) \leq 1$ | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010120.png" /> : $b _ { 2 } ( S ) \leq 1$ | ||
(confidence 0.48) | (confidence 0.48) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t12001033.png" /> : $[ \xi ^ { \alpha } , \xi ^ { b } ] = 2 \epsilon _ { \alpha b c } \xi ^ { c }$ | ||
| + | (confidence 0.47) | ||
<img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010108.png" /> : $sp ( 0 )$ | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010108.png" /> : $sp ( 0 )$ | ||
| Line 351: | Line 504: | ||
<img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t12001048.png" /> : $( S , g )$ | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t12001048.png" /> : $( S , g )$ | ||
| + | (confidence 0.31) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/a/a010/a010020/a0100204.png" /> : $\{ E _ { n _ { 1 } \ldots n _ { k } } \}$ | ||
| + | (confidence 0.31) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/a/a010/a010020/a0100207.png" /> : $\{ E _ { n _ { 1 } \ldots n _ { k } } \}$ | ||
(confidence 0.31) | (confidence 0.31) | ||
<img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t12001019.png" /> : $( C ( s ) , g )$ | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t12001019.png" /> : $( C ( s ) , g )$ | ||
(confidence 0.28) | (confidence 0.28) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t1200105.png" /> : $( C ( S ) , \overline { g } ) = ( R _ { + } \times S , d r ^ { 2 } + r ^ { 2 } g )$ | ||
| + | (confidence 0.27) | ||
<img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010106.png" /> : $G _ { 2 } / \operatorname { Sp } ( 1 ) , \quad F _ { 4 } / \operatorname { Sp } ( 3 ) , E _ { 6 } / \operatorname { SU } ( 6 ) , \quad E _ { 7 } / \operatorname { Spin } ( 12 ) , \quad E _ { 8 } / E _ { 7 }$ | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010106.png" /> : $G _ { 2 } / \operatorname { Sp } ( 1 ) , \quad F _ { 4 } / \operatorname { Sp } ( 3 ) , E _ { 6 } / \operatorname { SU } ( 6 ) , \quad E _ { 7 } / \operatorname { Spin } ( 12 ) , \quad E _ { 8 } / E _ { 7 }$ | ||
| Line 361: | Line 523: | ||
<img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t12001028.png" /> : $\{ I ^ { 1 } , P ^ { 2 } , \hat { P } \}$ | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t12001028.png" /> : $\{ I ^ { 1 } , P ^ { 2 } , \hat { P } \}$ | ||
(confidence 0.26) | (confidence 0.26) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/a/a010/a010080/a0100805.png" /> : $\{ A _ { n _ { 1 } } \ldots n _ { k } \}$ | ||
| + | (confidence 0.24) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t12001032.png" /> : $g ( \xi ^ { d } , \xi ^ { b } ) = \delta _ { c t b }$ | ||
| + | (confidence 0.22) | ||
<img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t12001088.png" /> : $\triangle ( S )$ | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t12001088.png" /> : $\triangle ( S )$ | ||
(confidence 0.20) | (confidence 0.20) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010105.png" /> : $SU ( m ) / S ( U ( m - 2 ) \times U ( 1 ) ) , SO ( k ) / SO ( k - 4 ) \times Sp ( 1 )$ | ||
| + | (confidence 0.19) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/a/a010/a010020/a01002010.png" /> : $m$ | ||
| + | (confidence 0.18) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/a/a010/a010020/a0100203.png" /> : $m$ | ||
| + | (confidence 0.18) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/a/a010/a010020/a01002019.png" /> : $m$ | ||
| + | (confidence 0.18) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/a/a010/a010020/a0100208.png" /> : $m$ | ||
| + | (confidence 0.18) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/a/a010/a010020/a01002011.png" /> : $m$ | ||
| + | (confidence 0.18) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/a/a010/a010020/a0100209.png" /> : $m$ | ||
| + | (confidence 0.18) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/a/a010/a010020/a01002012.png" /> : $m$ | ||
| + | (confidence 0.18) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/a/a010/a010020/a01002014.png" /> : $m$ | ||
| + | (confidence 0.18) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/a/a010/a010020/a01002016.png" /> : $m$ | ||
| + | (confidence 0.18) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/a/a010/a010020/a0100206.png" /> : $m$ | ||
| + | (confidence 0.18) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/a/a010/a010020/a01002018.png" /> : $m$ | ||
| + | (confidence 0.18) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/a/a010/a010080/a01008036.png" /> : $m$ | ||
| + | (confidence 0.18) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/a/a010/a010080/a01008016.png" /> : $m$ | ||
| + | (confidence 0.18) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/a/a010/a010080/a01008032.png" /> : $m$ | ||
| + | (confidence 0.18) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/a/a010/a010020/a0100205.png" /> : $P = \cup _ { n _ { 1 } , \ldots , n _ { k } , \ldots } \cap _ { k = 1 } ^ { \infty } E _ { x _ { 1 } \square \ldots n _ { k } }$ | ||
| + | (confidence 0.16) | ||
<img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t12001039.png" /> : $\Phi ^ { \mathscr { C } } ( Y ) = \nabla _ { Y } \xi ^ { \alpha }$ | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t12001039.png" /> : $\Phi ^ { \mathscr { C } } ( Y ) = \nabla _ { Y } \xi ^ { \alpha }$ | ||
| Line 369: | Line 585: | ||
<img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t12001038.png" /> : $\eta ^ { \mathscr { C } } ( Y ) = g ( \xi ^ { \alpha } , Y )$ | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t12001038.png" /> : $\eta ^ { \mathscr { C } } ( Y ) = g ( \xi ^ { \alpha } , Y )$ | ||
| + | (confidence 0.06) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/a/a010/a010080/a0100808.png" /> : $_ { 1 } , \ldots , A _ { k _ { 1 } } \ldots n _ { k } , \dots ,$ | ||
(confidence 0.06) | (confidence 0.06) | ||
| Line 375: | Line 594: | ||
<img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t12001041.png" /> : $ $ | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t12001041.png" /> : $ $ | ||
| + | (confidence 0.00) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t12001089.png" /> : $ $ | ||
| + | (confidence 0.00) | ||
| + | |||
| + | <img src ="https://www.encyclopediaofmath.org/legacyimages/a/a010/a010080/a0100807.png" /> : $ $ | ||
(confidence 0.00) | (confidence 0.00) | ||
Revision as of 23:10, 6 April 2019
This is a list of automatically classified LaTeX files. You can manually edit this list, your changes will currently not be considered and only overwritten though.
List
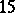 : $15$
(confidence 1.00)
: $15$
(confidence 1.00)
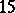 : $15$
(confidence 1.00)
: $15$
(confidence 1.00)
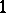 : $1$
(confidence 1.00)
: $1$
(confidence 1.00)
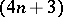 : $( 4 n + 3 )$
(confidence 1.00)
: $( 4 n + 3 )$
(confidence 1.00)
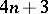 : $4 n + 3$
(confidence 1.00)
: $4 n + 3$
(confidence 1.00)
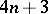 : $4 n + 3$
(confidence 1.00)
: $4 n + 3$
(confidence 1.00)
 : $11$
(confidence 1.00)
: $11$
(confidence 1.00)
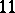 : $11$
(confidence 1.00)
: $11$
(confidence 1.00)
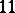 : $11$
(confidence 1.00)
: $11$
(confidence 1.00)
 : $2$
(confidence 1.00)
: $2$
(confidence 1.00)
 : $2$
(confidence 1.00)
: $2$
(confidence 1.00)
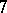 : $7$
(confidence 1.00)
: $7$
(confidence 1.00)
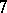 : $7$
(confidence 1.00)
: $7$
(confidence 1.00)
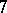 : $7$
(confidence 1.00)
: $7$
(confidence 1.00)
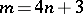 : $m = 4 n + 3$
(confidence 1.00)
: $m = 4 n + 3$
(confidence 1.00)
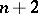 : $n + 2$
(confidence 1.00)
: $n + 2$
(confidence 1.00)
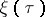 : $\xi ( \tau )$
(confidence 1.00)
: $\xi ( \tau )$
(confidence 1.00)
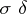 : $\sigma \delta$
(confidence 1.00)
: $\sigma \delta$
(confidence 1.00)
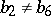 : $b _ { 2 } \neq b _ { 6 }$
(confidence 1.00)
: $b _ { 2 } \neq b _ { 6 }$
(confidence 1.00)
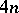 : $4 n$
(confidence 1.00)
: $4 n$
(confidence 1.00)
 : $\tau = ( \tau _ { 1 } , \tau _ { 2 } , \tau _ { 3 } ) \in R ^ { 3 }$
(confidence 1.00)
: $\tau = ( \tau _ { 1 } , \tau _ { 2 } , \tau _ { 3 } ) \in R ^ { 3 }$
(confidence 1.00)
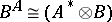 : $B ^ { A } \cong ( A ^ { * } \otimes B )$
(confidence 1.00)
: $B ^ { A } \cong ( A ^ { * } \otimes B )$
(confidence 1.00)
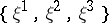 : $\{ \xi ^ { 1 } , \xi ^ { 2 } , \xi ^ { 3 } \}$
(confidence 1.00)
: $\{ \xi ^ { 1 } , \xi ^ { 2 } , \xi ^ { 3 } \}$
(confidence 1.00)
 : $\{ \xi ^ { 1 } , \xi ^ { 2 } , \xi ^ { 3 } \}$
(confidence 1.00)
: $\{ \xi ^ { 1 } , \xi ^ { 2 } , \xi ^ { 3 } \}$
(confidence 1.00)
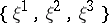 : $\{ \xi ^ { 1 } , \xi ^ { 2 } , \xi ^ { 3 } \}$
(confidence 1.00)
: $\{ \xi ^ { 1 } , \xi ^ { 2 } , \xi ^ { 3 } \}$
(confidence 1.00)
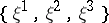 : $\{ \xi ^ { 1 } , \xi ^ { 2 } , \xi ^ { 3 } \}$
(confidence 1.00)
: $\{ \xi ^ { 1 } , \xi ^ { 2 } , \xi ^ { 3 } \}$
(confidence 1.00)
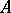 : $A$
(confidence 1.00)
: $A$
(confidence 1.00)
 : $A$
(confidence 1.00)
: $A$
(confidence 1.00)
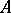 : $A$
(confidence 1.00)
: $A$
(confidence 1.00)
 : $A$
(confidence 1.00)
: $A$
(confidence 1.00)
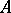 : $A$
(confidence 1.00)
: $A$
(confidence 1.00)
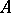 : $A$
(confidence 1.00)
: $A$
(confidence 1.00)
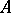 : $A$
(confidence 1.00)
: $A$
(confidence 1.00)
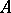 : $A$
(confidence 1.00)
: $A$
(confidence 1.00)
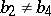 : $b _ { 2 } \neq b _ { 4 }$
(confidence 1.00)
: $b _ { 2 } \neq b _ { 4 }$
(confidence 1.00)
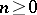 : $n \geq 0$
(confidence 1.00)
: $n \geq 0$
(confidence 1.00)
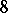 : $8$
(confidence 0.99)
: $8$
(confidence 0.99)
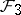 : $F _ { 3 }$
(confidence 0.99)
: $F _ { 3 }$
(confidence 0.99)
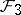 : $F _ { 3 }$
(confidence 0.99)
: $F _ { 3 }$
(confidence 0.99)
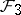 : $F _ { 3 }$
(confidence 0.99)
: $F _ { 3 }$
(confidence 0.99)
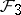 : $F _ { 3 }$
(confidence 0.99)
: $F _ { 3 }$
(confidence 0.99)
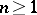 : $n \geq 1$
(confidence 0.99)
: $n \geq 1$
(confidence 0.99)
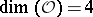 : $\operatorname { dim } ( O ) = 4$
(confidence 0.99)
: $\operatorname { dim } ( O ) = 4$
(confidence 0.99)
 : $3$
(confidence 0.99)
: $3$
(confidence 0.99)
 : $3$
(confidence 0.99)
: $3$
(confidence 0.99)
 : $3$
(confidence 0.99)
: $3$
(confidence 0.99)
 : $3$
(confidence 0.99)
: $3$
(confidence 0.99)
 : $3$
(confidence 0.99)
: $3$
(confidence 0.99)
 : $3$
(confidence 0.99)
: $3$
(confidence 0.99)
 : $3$
(confidence 0.99)
: $3$
(confidence 0.99)
 : $3$
(confidence 0.99)
: $3$
(confidence 0.99)
 : $3$
(confidence 0.99)
: $3$
(confidence 0.99)
 : $3$
(confidence 0.99)
: $3$
(confidence 0.99)
 : $3$
(confidence 0.99)
: $3$
(confidence 0.99)
 : $3$
(confidence 0.99)
: $3$
(confidence 0.99)
 : $3$
(confidence 0.99)
: $3$
(confidence 0.99)
 : $3$
(confidence 0.99)
: $3$
(confidence 0.99)
 : $3$
(confidence 0.99)
: $3$
(confidence 0.99)
 : $3$
(confidence 0.99)
: $3$
(confidence 0.99)
 : $3$
(confidence 0.99)
: $3$
(confidence 0.99)
 : $3$
(confidence 0.99)
: $3$
(confidence 0.99)
 : $3$
(confidence 0.99)
: $3$
(confidence 0.99)
 : $3$
(confidence 0.99)
: $3$
(confidence 0.99)
 : $3$
(confidence 0.99)
: $3$
(confidence 0.99)
 : $3$
(confidence 0.99)
: $3$
(confidence 0.99)
 : $3$
(confidence 0.99)
: $3$
(confidence 0.99)
 : $3$
(confidence 0.99)
: $3$
(confidence 0.99)
 : $3$
(confidence 0.99)
: $3$
(confidence 0.99)
 : $3$
(confidence 0.99)
: $3$
(confidence 0.99)
 : $z$
(confidence 0.99)
: $z$
(confidence 0.99)
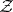 : $z$
(confidence 0.99)
: $z$
(confidence 0.99)
 : $\xi ( \tau ) = \tau _ { 1 } \xi ^ { 1 } + \tau _ { 2 } \xi ^ { 2 } + \tau _ { 3 } \xi ^ { 3 }$
(confidence 0.98)
: $\xi ( \tau ) = \tau _ { 1 } \xi ^ { 1 } + \tau _ { 2 } \xi ^ { 2 } + \tau _ { 3 } \xi ^ { 3 }$
(confidence 0.98)
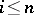 : $i < n$
(confidence 0.98)
: $i < n$
(confidence 0.98)
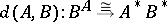 : $d ( A , B ) : B ^ { A } \cong A ^ { * } B ^ { * }$
(confidence 0.98)
: $d ( A , B ) : B ^ { A } \cong A ^ { * } B ^ { * }$
(confidence 0.98)
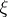 : $\xi$
(confidence 0.98)
: $\xi$
(confidence 0.98)
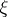 : $\xi$
(confidence 0.98)
: $\xi$
(confidence 0.98)
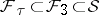 : $F _ { \tau } \subset F _ { 3 } \subset S$
(confidence 0.97)
: $F _ { \tau } \subset F _ { 3 } \subset S$
(confidence 0.97)
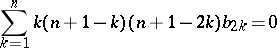 : $\sum _ { k = 1 } ^ { n } k ( n + 1 - k ) ( n + 1 - 2 k ) b _ { 2 k } = 0$
(confidence 0.96)
: $\sum _ { k = 1 } ^ { n } k ( n + 1 - k ) ( n + 1 - 2 k ) b _ { 2 k } = 0$
(confidence 0.96)
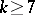 : $k > 7$
(confidence 0.96)
: $k > 7$
(confidence 0.96)
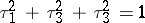 : $\tau _ { 1 } ^ { 2 } + \tau _ { 3 } ^ { 2 } + \tau _ { 3 } ^ { 2 } = 1$
(confidence 0.96)
: $\tau _ { 1 } ^ { 2 } + \tau _ { 3 } ^ { 2 } + \tau _ { 3 } ^ { 2 } = 1$
(confidence 0.96)
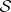 : $S$
(confidence 0.95)
: $S$
(confidence 0.95)
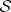 : $S$
(confidence 0.95)
: $S$
(confidence 0.95)
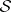 : $S$
(confidence 0.95)
: $S$
(confidence 0.95)
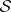 : $S$
(confidence 0.95)
: $S$
(confidence 0.95)
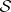 : $S$
(confidence 0.95)
: $S$
(confidence 0.95)
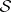 : $S$
(confidence 0.95)
: $S$
(confidence 0.95)
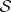 : $S$
(confidence 0.95)
: $S$
(confidence 0.95)
 : $S$
(confidence 0.95)
: $S$
(confidence 0.95)
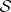 : $S$
(confidence 0.95)
: $S$
(confidence 0.95)
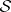 : $S$
(confidence 0.95)
: $S$
(confidence 0.95)
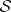 : $S$
(confidence 0.95)
: $S$
(confidence 0.95)
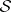 : $S$
(confidence 0.95)
: $S$
(confidence 0.95)
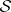 : $S$
(confidence 0.95)
: $S$
(confidence 0.95)
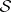 : $S$
(confidence 0.95)
: $S$
(confidence 0.95)
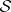 : $S$
(confidence 0.95)
: $S$
(confidence 0.95)
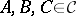 : $A , B , C \in C$
(confidence 0.95)
: $A , B , C \in C$
(confidence 0.95)
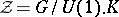 : $Z = G / U ( 1 ) . K$
(confidence 0.95)
: $Z = G / U ( 1 ) . K$
(confidence 0.95)
 : $> 7$
(confidence 0.95)
: $> 7$
(confidence 0.95)
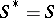 : $S ^ { * } = S$
(confidence 0.95)
: $S ^ { * } = S$
(confidence 0.95)
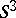 : $5 ^ { 3 }$
(confidence 0.94)
: $5 ^ { 3 }$
(confidence 0.94)
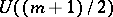 : $U ( ( m + 1 ) / 2 )$
(confidence 0.94)
: $U ( ( m + 1 ) / 2 )$
(confidence 0.94)
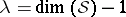 : $\lambda = \operatorname { dim } ( S ) - 1$
(confidence 0.94)
: $\lambda = \operatorname { dim } ( S ) - 1$
(confidence 0.94)
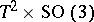 : $T ^ { 2 } \times SO ( 3 )$
(confidence 0.94)
: $T ^ { 2 } \times SO ( 3 )$
(confidence 0.94)
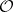 : $0$
(confidence 0.93)
: $0$
(confidence 0.93)
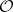 : $0$
(confidence 0.93)
: $0$
(confidence 0.93)
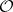 : $0$
(confidence 0.93)
: $0$
(confidence 0.93)
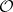 : $0$
(confidence 0.93)
: $0$
(confidence 0.93)
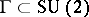 : $\Gamma \subset \operatorname { SU } ( 2 )$
(confidence 0.92)
: $\Gamma \subset \operatorname { SU } ( 2 )$
(confidence 0.92)
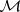 : $M$
(confidence 0.92)
: $M$
(confidence 0.92)
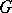 : $G$
(confidence 0.92)
: $G$
(confidence 0.92)
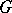 : $G$
(confidence 0.92)
: $G$
(confidence 0.92)
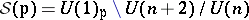 : $S ( p ) = U ( 1 ) _ { p } \backslash U ( n + 2 ) / U ( n )$
(confidence 0.92)
: $S ( p ) = U ( 1 ) _ { p } \backslash U ( n + 2 ) / U ( n )$
(confidence 0.92)
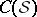 : $C ( S )$
(confidence 0.90)
: $C ( S )$
(confidence 0.90)
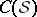 : $C ( S )$
(confidence 0.90)
: $C ( S )$
(confidence 0.90)
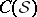 : $C ( S )$
(confidence 0.90)
: $C ( S )$
(confidence 0.90)
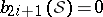 : $b _ { 2 i + 1 } ( S ) = 0$
(confidence 0.90)
: $b _ { 2 i + 1 } ( S ) = 0$
(confidence 0.90)
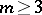 : $m > 3$
(confidence 0.89)
: $m > 3$
(confidence 0.89)
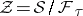 : $Z = S / F _ { \tau }$
(confidence 0.89)
: $Z = S / F _ { \tau }$
(confidence 0.89)
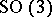 : $SO ( 3 )$
(confidence 0.88)
: $SO ( 3 )$
(confidence 0.88)
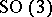 : $SO ( 3 )$
(confidence 0.88)
: $SO ( 3 )$
(confidence 0.88)
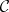 : $C$
(confidence 0.87)
: $C$
(confidence 0.87)
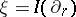 : $\xi = I ( \partial _ { r } )$
(confidence 0.87)
: $\xi = I ( \partial _ { r } )$
(confidence 0.87)
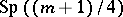 : $\operatorname { sp } ( ( m + 1 ) / 4 )$
(confidence 0.86)
: $\operatorname { sp } ( ( m + 1 ) / 4 )$
(confidence 0.86)
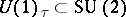 : $U ( 1 ) _ { \tau } \subset SU ( 2 )$
(confidence 0.82)
: $U ( 1 ) _ { \tau } \subset SU ( 2 )$
(confidence 0.82)
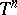 : $T ^ { n }$
(confidence 0.82)
: $T ^ { n }$
(confidence 0.82)
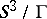 : $S ^ { 3 } / \Gamma$
(confidence 0.82)
: $S ^ { 3 } / \Gamma$
(confidence 0.82)
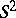 : $5 ^ { 2 }$
(confidence 0.80)
: $5 ^ { 2 }$
(confidence 0.80)
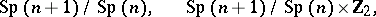 : $\operatorname { Sp } ( n + 1 ) / \operatorname { Sp } ( n ) , \quad \operatorname { Sp } ( n + 1 ) / \operatorname { Sp } ( n ) \times Z _ { 2 }$
(confidence 0.80)
: $\operatorname { Sp } ( n + 1 ) / \operatorname { Sp } ( n ) , \quad \operatorname { Sp } ( n + 1 ) / \operatorname { Sp } ( n ) \times Z _ { 2 }$
(confidence 0.80)
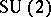 : $SU ( 2 )$
(confidence 0.79)
: $SU ( 2 )$
(confidence 0.79)
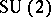 : $SU ( 2 )$
(confidence 0.79)
: $SU ( 2 )$
(confidence 0.79)
 : $T ^ { 2 } \times Sp ( 1 )$
(confidence 0.79)
: $T ^ { 2 } \times Sp ( 1 )$
(confidence 0.79)
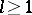 : $l > 1$
(confidence 0.77)
: $l > 1$
(confidence 0.77)
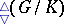 : $\triangle ( G / K )$
(confidence 0.77)
: $\triangle ( G / K )$
(confidence 0.77)
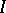 : $1$
(confidence 0.77)
: $1$
(confidence 0.77)
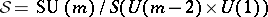 : $S = SU ( m ) / S ( U ( m - 2 ) \times U ( 1 ) )$
(confidence 0.75)
: $S = SU ( m ) / S ( U ( m - 2 ) \times U ( 1 ) )$
(confidence 0.75)
 : $5$
(confidence 0.74)
: $5$
(confidence 0.74)
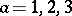 : $\alpha = 1,2,3$
(confidence 0.74)
: $\alpha = 1,2,3$
(confidence 0.74)
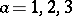 : $\alpha = 1,2,3$
(confidence 0.74)
: $\alpha = 1,2,3$
(confidence 0.74)
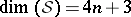 : $\operatorname { dim } ( S ) = 4 n + 3$
(confidence 0.73)
: $\operatorname { dim } ( S ) = 4 n + 3$
(confidence 0.73)
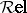 : $R e l$
(confidence 0.69)
: $R e l$
(confidence 0.69)
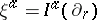 : $\xi ^ { \alpha } = I ^ { \alpha } ( \partial _ { r } )$
(confidence 0.67)
: $\xi ^ { \alpha } = I ^ { \alpha } ( \partial _ { r } )$
(confidence 0.67)
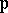 : $p$
(confidence 0.64)
: $p$
(confidence 0.64)
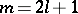 : $m = 2 l + 1$
(confidence 0.61)
: $m = 2 l + 1$
(confidence 0.61)
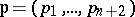 : $p = ( p _ { 1 } , \dots , p _ { n } + 2 )$
(confidence 0.61)
: $p = ( p _ { 1 } , \dots , p _ { n } + 2 )$
(confidence 0.61)
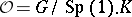 : $O = G / Sp ( 1 ) . K$
(confidence 0.57)
: $O = G / Sp ( 1 ) . K$
(confidence 0.57)
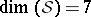 : $\operatorname { lim } ( S ) = 7$
(confidence 0.53)
: $\operatorname { lim } ( S ) = 7$
(confidence 0.53)
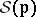 : $S ( p )$
(confidence 0.52)
: $S ( p )$
(confidence 0.52)
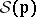 : $S ( p )$
(confidence 0.52)
: $S ( p )$
(confidence 0.52)
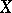 : $X$
(confidence 0.51)
: $X$
(confidence 0.51)
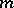 : $m$
(confidence 0.50)
: $m$
(confidence 0.50)
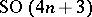 : $SO ( 4 n + 3 )$
(confidence 0.49)
: $SO ( 4 n + 3 )$
(confidence 0.49)
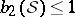 : $b _ { 2 } ( S ) \leq 1$
(confidence 0.48)
: $b _ { 2 } ( S ) \leq 1$
(confidence 0.48)
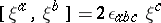 : $[ \xi ^ { \alpha } , \xi ^ { b } ] = 2 \epsilon _ { \alpha b c } \xi ^ { c }$
(confidence 0.47)
: $[ \xi ^ { \alpha } , \xi ^ { b } ] = 2 \epsilon _ { \alpha b c } \xi ^ { c }$
(confidence 0.47)
 : $sp ( 0 )$
(confidence 0.44)
: $sp ( 0 )$
(confidence 0.44)
 : $35$
(confidence 0.42)
: $35$
(confidence 0.42)
 : $35$
(confidence 0.42)
: $35$
(confidence 0.42)
 : $35$
(confidence 0.42)
: $35$
(confidence 0.42)
 : $35$
(confidence 0.42)
: $35$
(confidence 0.42)
 : $35$
(confidence 0.42)
: $35$
(confidence 0.42)
 : $35$
(confidence 0.42)
: $35$
(confidence 0.42)
 : $35$
(confidence 0.42)
: $35$
(confidence 0.42)
 : $( - ) ^ { * } : C ^ { 0 p } \rightarrow C$
(confidence 0.39)
: $( - ) ^ { * } : C ^ { 0 p } \rightarrow C$
(confidence 0.39)
 : $s = s ( ( A ^ { * } ) ^ { ( B ^ { * } ) } , ( B ^ { * } ) ^ { ( C ^ { * } ) } )$
(confidence 0.37)
: $s = s ( ( A ^ { * } ) ^ { ( B ^ { * } ) } , ( B ^ { * } ) ^ { ( C ^ { * } ) } )$
(confidence 0.37)
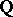 : $5$
(confidence 0.36)
: $5$
(confidence 0.36)
 : $( S , g )$
(confidence 0.31)
: $( S , g )$
(confidence 0.31)
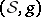 : $( S , g )$
(confidence 0.31)
: $( S , g )$
(confidence 0.31)
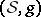 : $( S , g )$
(confidence 0.31)
: $( S , g )$
(confidence 0.31)
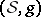 : $( S , g )$
(confidence 0.31)
: $( S , g )$
(confidence 0.31)
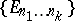 : $\{ E _ { n _ { 1 } \ldots n _ { k } } \}$
(confidence 0.31)
: $\{ E _ { n _ { 1 } \ldots n _ { k } } \}$
(confidence 0.31)
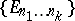 : $\{ E _ { n _ { 1 } \ldots n _ { k } } \}$
(confidence 0.31)
: $\{ E _ { n _ { 1 } \ldots n _ { k } } \}$
(confidence 0.31)
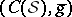 : $( C ( s ) , g )$
(confidence 0.28)
: $( C ( s ) , g )$
(confidence 0.28)
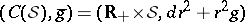 : $( C ( S ) , \overline { g } ) = ( R _ { + } \times S , d r ^ { 2 } + r ^ { 2 } g )$
(confidence 0.27)
: $( C ( S ) , \overline { g } ) = ( R _ { + } \times S , d r ^ { 2 } + r ^ { 2 } g )$
(confidence 0.27)
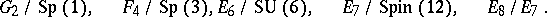 : $G _ { 2 } / \operatorname { Sp } ( 1 ) , \quad F _ { 4 } / \operatorname { Sp } ( 3 ) , E _ { 6 } / \operatorname { SU } ( 6 ) , \quad E _ { 7 } / \operatorname { Spin } ( 12 ) , \quad E _ { 8 } / E _ { 7 }$
(confidence 0.27)
: $G _ { 2 } / \operatorname { Sp } ( 1 ) , \quad F _ { 4 } / \operatorname { Sp } ( 3 ) , E _ { 6 } / \operatorname { SU } ( 6 ) , \quad E _ { 7 } / \operatorname { Spin } ( 12 ) , \quad E _ { 8 } / E _ { 7 }$
(confidence 0.27)
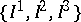 : $\{ I ^ { 1 } , P ^ { 2 } , \hat { P } \}$
(confidence 0.26)
: $\{ I ^ { 1 } , P ^ { 2 } , \hat { P } \}$
(confidence 0.26)
 : $\{ A _ { n _ { 1 } } \ldots n _ { k } \}$
(confidence 0.24)
: $\{ A _ { n _ { 1 } } \ldots n _ { k } \}$
(confidence 0.24)
 : $g ( \xi ^ { d } , \xi ^ { b } ) = \delta _ { c t b }$
(confidence 0.22)
: $g ( \xi ^ { d } , \xi ^ { b } ) = \delta _ { c t b }$
(confidence 0.22)
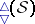 : $\triangle ( S )$
(confidence 0.20)
: $\triangle ( S )$
(confidence 0.20)
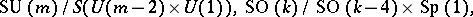 : $SU ( m ) / S ( U ( m - 2 ) \times U ( 1 ) ) , SO ( k ) / SO ( k - 4 ) \times Sp ( 1 )$
(confidence 0.19)
: $SU ( m ) / S ( U ( m - 2 ) \times U ( 1 ) ) , SO ( k ) / SO ( k - 4 ) \times Sp ( 1 )$
(confidence 0.19)
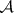 : $m$
(confidence 0.18)
: $m$
(confidence 0.18)
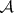 : $m$
(confidence 0.18)
: $m$
(confidence 0.18)
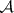 : $m$
(confidence 0.18)
: $m$
(confidence 0.18)
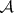 : $m$
(confidence 0.18)
: $m$
(confidence 0.18)
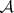 : $m$
(confidence 0.18)
: $m$
(confidence 0.18)
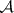 : $m$
(confidence 0.18)
: $m$
(confidence 0.18)
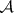 : $m$
(confidence 0.18)
: $m$
(confidence 0.18)
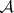 : $m$
(confidence 0.18)
: $m$
(confidence 0.18)
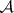 : $m$
(confidence 0.18)
: $m$
(confidence 0.18)
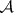 : $m$
(confidence 0.18)
: $m$
(confidence 0.18)
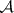 : $m$
(confidence 0.18)
: $m$
(confidence 0.18)
 : $m$
(confidence 0.18)
: $m$
(confidence 0.18)
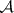 : $m$
(confidence 0.18)
: $m$
(confidence 0.18)
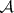 : $m$
(confidence 0.18)
: $m$
(confidence 0.18)
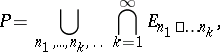 : $P = \cup _ { n _ { 1 } , \ldots , n _ { k } , \ldots } \cap _ { k = 1 } ^ { \infty } E _ { x _ { 1 } \square \ldots n _ { k } }$
(confidence 0.16)
: $P = \cup _ { n _ { 1 } , \ldots , n _ { k } , \ldots } \cap _ { k = 1 } ^ { \infty } E _ { x _ { 1 } \square \ldots n _ { k } }$
(confidence 0.16)
 : $\Phi ^ { \mathscr { C } } ( Y ) = \nabla _ { Y } \xi ^ { \alpha }$
(confidence 0.14)
: $\Phi ^ { \mathscr { C } } ( Y ) = \nabla _ { Y } \xi ^ { \alpha }$
(confidence 0.14)
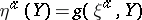 : $\eta ^ { \mathscr { C } } ( Y ) = g ( \xi ^ { \alpha } , Y )$
(confidence 0.06)
: $\eta ^ { \mathscr { C } } ( Y ) = g ( \xi ^ { \alpha } , Y )$
(confidence 0.06)
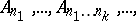 : $_ { 1 } , \ldots , A _ { k _ { 1 } } \ldots n _ { k } , \dots ,$
(confidence 0.06)
: $_ { 1 } , \ldots , A _ { k _ { 1 } } \ldots n _ { k } , \dots ,$
(confidence 0.06)
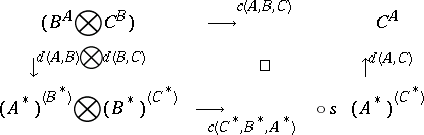 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
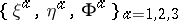 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
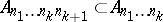 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
Maximilian Janisch/latexlist. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Maximilian_Janisch/latexlist&oldid=43674