User:Maximilian Janisch/latexlist

This is a list of automatically classified LaTeX files. You can manually edit this list, your changes will currently not be considered and only overwritten though.

List

 : $ $ (confidence 0)

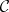 : $ $ (confidence 0)

 : $ $ (confidence 0)

 : $ $ (confidence 0)

 : $ $ (confidence 0)

 : $( - ) ^ { * } : C ^ { 0 p } \rightarrow C$ (confidence 0.2558360957702055)

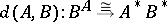 : $d ( A , B ) : B ^ { A } \cong A ^ { * } B ^ { * }$ (confidence 0.7513806030787462)

 : $ $ (confidence 0.11977224303966238)

 : $ $ (confidence 0)

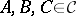 : $A , B , C \in C$ (confidence 0.9874941305418984)

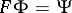 : $F \Phi = \Psi$ (confidence 0.4805759882593679)

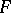 : $r$ (confidence 0.12389555304878641)

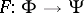 : $\Phi \rightarrow \Psi$ (confidence 0.7790935007842552)

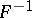 : $F ^ { \prime }$ (confidence 0.11142785371739461)

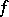 : $t$ (confidence 0.5074253082275391)

 : $ $ (confidence 0)

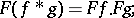 : $F ( f ^ { * } g ) = F f . F g$ (confidence 0.6819218234974772)

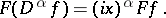 : $F ( D ^ { \alpha } f ) = ( i x ) ^ { \alpha } F f$ (confidence 0.7705838634334625)

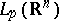 : $L _ { p } ( R ^ { n } )$ (confidence 0.8757486845276239)

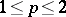 : $\leq p \leq 2$ (confidence 0.27530124031725317)

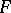 : $r$ (confidence 0.12389555304878641)

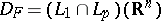 : $D _ { F } = ( L _ { 1 } \cap L _ { p } ) ( R ^ { n } )$ (confidence 0.26241861040115294)

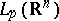 : $L _ { p } ( R ^ { n } )$ (confidence 0.8757486845276239)

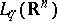 : $L _ { \varphi } ( R ^ { n } )$ (confidence 0.2310629780771597)

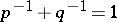 : $p ^ { - 1 } + q ^ { - 1 } = 1$ (confidence 0.9973485092235681)

 : $r$ (confidence 0.12389555304878641)

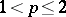 : $1 < p \leq 2$ (confidence 0.9964472555859636)

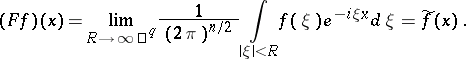 : $ $ (confidence 0)

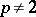 : $p \neq 2$ (confidence 0.9978736607221192)

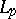 : $x$ (confidence 0.12837346605452638)

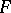 : $r$ (confidence 0.12389555304878641)

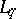 : $x$ (confidence 0.33397466109307317)

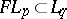 : $F L _ { p } \subset l _ { q }$ (confidence 0.4314001351435635)

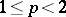 : $\leq p < 2$ (confidence 0.3140245219383027)

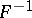 : $F ^ { \prime }$ (confidence 0.11142785371739461)

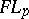 : $F L y$ (confidence 0.9421360432265639)

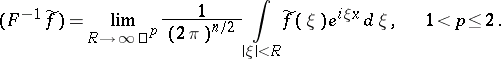 : $( F ^ { - 1 } \tilde { f } ) = \operatorname { lim } _ { R \rightarrow \infty } \frac { 1 } { ( 2 \pi ) ^ { n / 2 } } \int _ { | \xi | < R } \tilde { f } ( \xi ) e ^ { i \xi x } d \xi , \quad 1 < p \leq 2$ (confidence 0.16566260709655076)

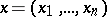 : $x = ( x _ { 1 } , \ldots , x _ { n } )$ (confidence 0.08374742170778082)

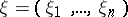 : $\xi = ( \xi _ { 1 } , \ldots , \xi _ { n } )$ (confidence 0.529109226067534)

 : $x$ (confidence 0.6640530313855136)

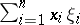 : $\sum _ { i = 1 } ^ { 8 } x _ { i } \xi$ (confidence 0.11581139252073573)

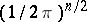 : $( 1 / 2 \pi ) ^ { n / 2 }$ (confidence 0.9994450835812325)

 : $ $ (confidence 0)

 : $ $ (confidence 0)

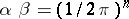 : $\beta = ( 1 / 2 \pi ) ^ { x }$ (confidence 0.9130163734938249)

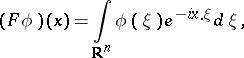 : $( F \phi ) ( x ) = \int _ { R ^ { n } } \phi ( \xi ) e ^ { - i x \cdot \xi } d \xi$ (confidence 0.3057988248146818)

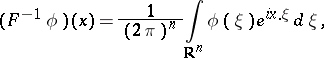 : $( F ^ { - 1 } \phi ) ( x ) = \frac { 1 } { ( 2 \pi ) ^ { n } } \int _ { R ^ { n } } \phi ( \xi ) e ^ { i x . \xi } d \xi$ (confidence 0.5024619621936454)

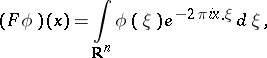 : $( F \phi ) ( x ) = \int _ { R ^ { n } } \phi ( \xi ) e ^ { - 2 \pi i x . \xi } d \xi$ (confidence 0.15634412476601953)

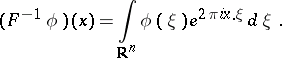 : $( F ^ { - 1 } \phi ) ( x ) = \int _ { R ^ { n } } \phi ( \xi ) e ^ { 2 \pi i x . \xi } d \xi$ (confidence 0.08016216799456224)

 : $L _ { 2 } ( R ^ { * } )$ (confidence 0.3347255664604998)