Difference between revisions of "Tangent vector"
(TeX (partially done)) |
|||
| Line 1: | Line 1: | ||
| − | Let | + | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t0922001.png" /> be a [[Differentiable manifold|differentiable manifold]], and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t0922002.png" /> be the algebra of smooth real-valued functions on it. A tangent vector to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t0922003.png" /> at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t0922004.png" /> is an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t0922005.png" />-linear mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t0922006.png" /> such that |
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t0922007.png" /></td> <td valign="top" style="width:5%;text-align:right;">(a1)</td></tr></table> | |
| − | |||
| − | |||
| − | For this definition one can equally well (in fact, better) use the ring of germs of smooth functions | + | For this definition one can equally well (in fact, better) use the ring of germs of smooth functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t0922008.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t0922009.png" /> at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220010.png" />. |
| − | The tangent vectors to | + | The tangent vectors to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220011.png" /> at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220012.png" /> form a vector space over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220013.png" /> of dimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220014.png" />. It is denoted by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220015.png" />. |
| − | Let | + | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220016.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220017.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220018.png" /> is a system of coordinates on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220019.png" /> near <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220020.png" />. The <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220021.png" />-th partial derivative at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220022.png" /> with respect to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220023.png" /> is the tangent vector |
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220024.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | where the right hand-side is the usual partial derivative of the function | + | where the right hand-side is the usual partial derivative of the function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220025.png" /> in the variables <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220026.png" />, at the point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220027.png" />. One has <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220028.png" /> (the Kronecker delta) and the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220029.png" /> form a basis for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220030.png" />. |
| − | This basis for | + | This basis for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220031.png" /> determined by the coordinate system <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220032.png" /> is often denoted by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220033.png" />. |
| − | A cotangent vector at | + | A cotangent vector at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220034.png" /> is an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220035.png" />-linear mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220036.png" /> such that the cotangent space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220037.png" /> at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220038.png" /> is the dual vector space to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220039.png" />. The dual basis to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220040.png" /> is denoted by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220041.png" />. One has |
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220042.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | The disjoint union | + | The disjoint union <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220043.png" /> of the tangent spaces <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220044.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220045.png" />, together with the projection <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220046.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220047.png" /> if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220048.png" />, can be given the structure of a differentiable [[Vector bundle|vector bundle]], the [[Tangent bundle|tangent bundle]]. |
| − | Similarly, the cotangent spaces | + | Similarly, the cotangent spaces <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220049.png" /> form a vector bundle <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220050.png" /> dual to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220051.png" />, called the cotangent bundle. The sections of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220052.png" /> are the vector fields on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220053.png" />, the sections of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220054.png" /> are differentiable <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220056.png" />-forms on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220057.png" />. |
| − | Let | + | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220058.png" /> be a mapping of differentiable manifolds and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220059.png" /> be the induced mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220060.png" />. For a tangent vector <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220061.png" /> at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220062.png" />, composition with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220063.png" /> gives an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220064.png" />-linear mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220065.png" /> which is a tangent vector to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220066.png" /> at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220067.png" />. This defines a homomorphism of vector spaces <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220068.png" /> and a vector bundle morphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220069.png" />. |
| − | In case | + | In case <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220070.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220071.png" /> with global coordinates <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220072.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220073.png" />, respectively, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220074.png" /> is given by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220075.png" /> differentiable functions and at each <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220076.png" />, |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"> | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220077.png" /></td> </tr></table> |
| − | so that the matrix of | + | so that the matrix of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220078.png" /> with respect to the basis <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220079.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220080.png" /> and the basis <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220081.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220082.png" /> is given by the [[Jacobi matrix|Jacobi matrix]] of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220083.png" /> at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220084.png" />. |
| − | Now, let | + | Now, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220085.png" /> be an imbedded manifold. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220086.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220087.png" /> be a smooth curve in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220088.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220089.png" />. Then |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"> | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220090.png" /></td> <td valign="top" style="width:5%;text-align:right;">(a2)</td></tr></table> |
| − | All tangent vectors in | + | All tangent vectors in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220091.png" /> arise in this way. Identifying the vector (a2) with the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220092.png" />-vector <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220093.png" />, viewed as a directed line segment starting in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220094.png" />, one recovers the intuitive picture of the tangent space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220095.png" /> as the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220096.png" />-plane in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220097.png" /> tangent to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220098.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t09220099.png" />. |
| − | A vector field on a manifold | + | A vector field on a manifold <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t092200100.png" /> can be defined as a derivation (cf. [[Derivation in a ring|Derivation in a ring]]) in the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t092200101.png" />-algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t092200102.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t092200103.png" />. Composition with the evaluation mappings <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t092200104.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t092200105.png" />, yields a family of tangent vectors <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t092200106.png" />, so that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t092200107.png" /> "becomes" a section of the [[Tangent bundle|tangent bundle]]. Given local coordinates <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t092200108.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t092200109.png" /> can locally be written as |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"> | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t092200110.png" /></td> </tr></table> |
| − | and if a function | + | and if a function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t092200111.png" /> in local coordinates is given by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t092200112.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t092200113.png" /> is the function given in local coordinates by the expression |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"> | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t092200114.png" /></td> </tr></table> |
| − | showing once more the convenience of the " / x" notation for tangent vectors. (Of course, in practice one uses a bit more abuse of notation and writes | + | showing once more the convenience of the " / x" notation for tangent vectors. (Of course, in practice one uses a bit more abuse of notation and writes <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t092200115.png" /> instead of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t092200116.png" />.) |
| − | Let | + | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t092200117.png" /> be the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t092200118.png" />-algebra of germs of smooth functions at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t092200119.png" /> (cf. [[Germ|Germ]]). Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t092200120.png" /> be the ideal of germs that vanish at zero, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t092200121.png" /> the ideal generated by all products <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t092200122.png" /> for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t092200123.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t092200124.png" /> are local coordinates at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t092200125.png" /> so that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t092200126.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t092200127.png" /> is generated as an ideal in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t092200128.png" /> by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t092200129.png" />, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t092200130.png" /> by the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t092200131.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t092200132.png" />. In fact, the quotient ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t092200133.png" /> is the power series ring in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t092200134.png" /> variables over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t092200135.png" />. Here <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t092200136.png" /> is the ideal of flat function germs. (A smooth function is flat at a point if it vanishes there with all its derivatives (an example is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t092200137.png" /> at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t092200138.png" />); the "Taylor expansion mapping" <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t092200139.png" /> is surjective, a very special consequence of the [[Whitney extension theorem|Whitney extension theorem]].) |
| − | Now, let | + | Now, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t092200140.png" /> be a tangent vector of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t092200141.png" /> at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t092200142.png" />. Then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t092200143.png" /> by (a1) for all constant functions in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t092200144.png" />. Also <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t092200145.png" />, again by (a1). Thus, each <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t092200146.png" /> defines an element in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t092200147.png" />, which is of dimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t092200148.png" /> because <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t092200149.png" /> has dimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t092200150.png" /> (and that element uniquely determines <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t092200151.png" />). Moreover, the tangent vectors <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t092200152.png" /> clearly define <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t092200153.png" /> linearly independent elements in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t092200154.png" /> (because <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t092200155.png" />). Thus, |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"> | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t092200156.png" /></td> </tr></table> |
| − | the dual space of | + | the dual space of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092200/t092200157.png" />. This point of view is more generally applicable and serves as the definition of tangent space in analytic and algebraic geometry, cf. [[Analytic space|Analytic space]]; [[Zariski tangent space|Zariski tangent space]]. |
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> R. Hermann, "Geometry, physics, and systems" , M. Dekker (1973) {{MR|0494183}} {{ZBL|0285.58001}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> R.L. Bishop, R.J. Crittenden, "Geometry of manifolds" , Acad. Press (1964) {{MR|0169148}} {{ZBL|0132.16003}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> M.W. Hirsch, "Differential topology" , Springer (1976) pp. 4, 78 {{MR|0448362}} {{ZBL|0356.57001}} </TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> S.P. Novikov, A.T. Fomenko, "Basic elements of differential geometry and topology" , Kluwer (1991) (Translated from Russian) {{MR|1135798}} {{ZBL|0711.53001}} </TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> Yu. Borisovich, N. Bliznyakov, Ya. Izrailevich, T. Fomenko, "Introduction to topology" , Kluwer (1993) (Translated from Russian) {{MR|1450091}} {{MR|0824983}} {{MR|0591670}} {{ZBL|0836.57001}} {{ZBL|0834.57001}} {{ZBL|0478.57001}} </TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> R. Hermann, "Geometry, physics, and systems" , M. Dekker (1973) {{MR|0494183}} {{ZBL|0285.58001}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> R.L. Bishop, R.J. Crittenden, "Geometry of manifolds" , Acad. Press (1964) {{MR|0169148}} {{ZBL|0132.16003}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> M.W. Hirsch, "Differential topology" , Springer (1976) pp. 4, 78 {{MR|0448362}} {{ZBL|0356.57001}} </TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> S.P. Novikov, A.T. Fomenko, "Basic elements of differential geometry and topology" , Kluwer (1991) (Translated from Russian) {{MR|1135798}} {{ZBL|0711.53001}} </TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> Yu. Borisovich, N. Bliznyakov, Ya. Izrailevich, T. Fomenko, "Introduction to topology" , Kluwer (1993) (Translated from Russian) {{MR|1450091}} {{MR|0824983}} {{MR|0591670}} {{ZBL|0836.57001}} {{ZBL|0834.57001}} {{ZBL|0478.57001}} </TD></TR></table> | ||
Revision as of 15:31, 21 May 2017
Let 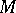 be a differentiable manifold, and let
be a differentiable manifold, and let 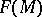 be the algebra of smooth real-valued functions on it. A tangent vector to
be the algebra of smooth real-valued functions on it. A tangent vector to 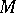 at
at 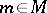 is an
is an 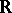 -linear mapping
-linear mapping 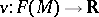 such that
such that
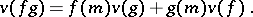 | (a1) |
For this definition one can equally well (in fact, better) use the ring of germs of smooth functions 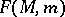 on
on 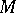 at
at  .
.
The tangent vectors to 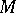 at
at 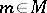 form a vector space over
form a vector space over  of dimension
of dimension 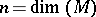 . It is denoted by
. It is denoted by 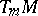 .
.
Let  ,
, 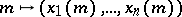 , where
, where 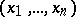 is a system of coordinates on
is a system of coordinates on  near
near 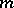 . The
. The 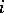 -th partial derivative at
-th partial derivative at 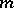 with respect to
with respect to  is the tangent vector
is the tangent vector
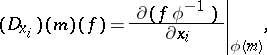 |
where the right hand-side is the usual partial derivative of the function 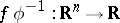 in the variables
in the variables  , at the point
, at the point 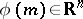 . One has
. One has  (the Kronecker delta) and the
(the Kronecker delta) and the 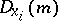 form a basis for
form a basis for 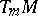 .
.
This basis for  determined by the coordinate system
determined by the coordinate system 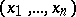 is often denoted by
is often denoted by 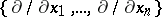 .
.
A cotangent vector at  is an
is an  -linear mapping
-linear mapping 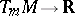 such that the cotangent space
such that the cotangent space 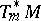 at
at  is the dual vector space to
is the dual vector space to 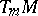 . The dual basis to
. The dual basis to 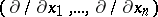 is denoted by
is denoted by 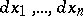 . One has
. One has
 |
The disjoint union 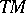 of the tangent spaces
of the tangent spaces  ,
,  , together with the projection
, together with the projection 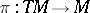 ,
, 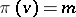 if
if  , can be given the structure of a differentiable vector bundle, the tangent bundle.
, can be given the structure of a differentiable vector bundle, the tangent bundle.
Similarly, the cotangent spaces 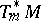 form a vector bundle
form a vector bundle  dual to
dual to  , called the cotangent bundle. The sections of
, called the cotangent bundle. The sections of  are the vector fields on
are the vector fields on  , the sections of
, the sections of 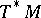 are differentiable
are differentiable  -forms on
-forms on 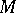 .
.
Let 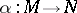 be a mapping of differentiable manifolds and let
be a mapping of differentiable manifolds and let 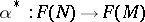 be the induced mapping
be the induced mapping 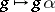 . For a tangent vector
. For a tangent vector 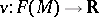 at
at  , composition with
, composition with 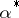 gives an
gives an 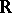 -linear mapping
-linear mapping 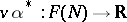 which is a tangent vector to
which is a tangent vector to 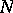 at
at  . This defines a homomorphism of vector spaces
. This defines a homomorphism of vector spaces  and a vector bundle morphism
and a vector bundle morphism  .
.
In case 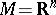 and
and 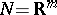 with global coordinates
with global coordinates  and
and 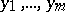 , respectively,
, respectively, 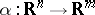 is given by
is given by 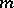 differentiable functions and at each
differentiable functions and at each  ,
,
 |
so that the matrix of  with respect to the basis
with respect to the basis  of
of 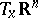 and the basis
and the basis 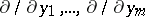 of
of 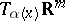 is given by the Jacobi matrix of
is given by the Jacobi matrix of 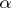 at
at  .
.
Now, let 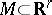 be an imbedded manifold. Let
be an imbedded manifold. Let  ,
, 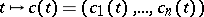 be a smooth curve in
be a smooth curve in 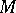 ,
, 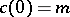 . Then
. Then
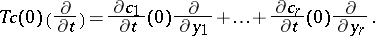 | (a2) |
All tangent vectors in  arise in this way. Identifying the vector (a2) with the
arise in this way. Identifying the vector (a2) with the  -vector
-vector 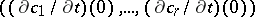 , viewed as a directed line segment starting in
, viewed as a directed line segment starting in  , one recovers the intuitive picture of the tangent space
, one recovers the intuitive picture of the tangent space  as the
as the  -plane in
-plane in  tangent to
tangent to 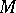 in
in 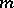 .
.
A vector field on a manifold  can be defined as a derivation (cf. Derivation in a ring) in the
can be defined as a derivation (cf. Derivation in a ring) in the 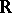 -algebra
-algebra 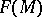 ,
,  . Composition with the evaluation mappings
. Composition with the evaluation mappings 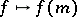 ,
, 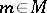 , yields a family of tangent vectors
, yields a family of tangent vectors  , so that
, so that 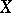 "becomes" a section of the tangent bundle. Given local coordinates
"becomes" a section of the tangent bundle. Given local coordinates  ,
,  can locally be written as
can locally be written as
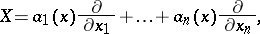 |
and if a function 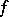 in local coordinates is given by
in local coordinates is given by 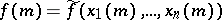 , then
, then 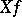 is the function given in local coordinates by the expression
is the function given in local coordinates by the expression
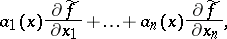 |
showing once more the convenience of the " / x" notation for tangent vectors. (Of course, in practice one uses a bit more abuse of notation and writes 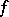 instead of
instead of 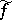 .)
.)
Let 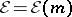 be the
be the 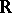 -algebra of germs of smooth functions at
-algebra of germs of smooth functions at 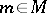 (cf. Germ). Let
(cf. Germ). Let 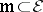 be the ideal of germs that vanish at zero, and
be the ideal of germs that vanish at zero, and  the ideal generated by all products
the ideal generated by all products 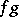 for
for  . If
. If  are local coordinates at
are local coordinates at 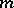 so that
so that  ,
, 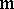 is generated as an ideal in
is generated as an ideal in  by
by 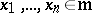 , and
, and  by the
by the  ,
, 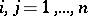 . In fact, the quotient ring
. In fact, the quotient ring 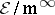 is the power series ring in
is the power series ring in  variables over
variables over 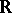 . Here
. Here 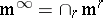 is the ideal of flat function germs. (A smooth function is flat at a point if it vanishes there with all its derivatives (an example is
is the ideal of flat function germs. (A smooth function is flat at a point if it vanishes there with all its derivatives (an example is 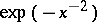 at
at  ); the "Taylor expansion mapping"
); the "Taylor expansion mapping" 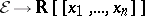 is surjective, a very special consequence of the Whitney extension theorem.)
is surjective, a very special consequence of the Whitney extension theorem.)
Now, let  be a tangent vector of
be a tangent vector of  at
at 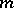 . Then
. Then 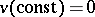 by (a1) for all constant functions in
by (a1) for all constant functions in  . Also
. Also 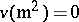 , again by (a1). Thus, each
, again by (a1). Thus, each  defines an element in
defines an element in 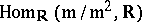 , which is of dimension
, which is of dimension  because
because 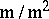 has dimension
has dimension  (and that element uniquely determines
(and that element uniquely determines  ). Moreover, the tangent vectors
). Moreover, the tangent vectors  clearly define
clearly define  linearly independent elements in
linearly independent elements in 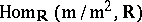 (because
(because  ). Thus,
). Thus,
 |
the dual space of 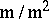 . This point of view is more generally applicable and serves as the definition of tangent space in analytic and algebraic geometry, cf. Analytic space; Zariski tangent space.
. This point of view is more generally applicable and serves as the definition of tangent space in analytic and algebraic geometry, cf. Analytic space; Zariski tangent space.
References
| [a1] | R. Hermann, "Geometry, physics, and systems" , M. Dekker (1973) MR0494183 Zbl 0285.58001 |
| [a2] | R.L. Bishop, R.J. Crittenden, "Geometry of manifolds" , Acad. Press (1964) MR0169148 Zbl 0132.16003 |
| [a3] | M.W. Hirsch, "Differential topology" , Springer (1976) pp. 4, 78 MR0448362 Zbl 0356.57001 |
| [a4] | S.P. Novikov, A.T. Fomenko, "Basic elements of differential geometry and topology" , Kluwer (1991) (Translated from Russian) MR1135798 Zbl 0711.53001 |
| [a5] | Yu. Borisovich, N. Bliznyakov, Ya. Izrailevich, T. Fomenko, "Introduction to topology" , Kluwer (1993) (Translated from Russian) MR1450091 MR0824983 MR0591670 Zbl 0836.57001 Zbl 0834.57001 Zbl 0478.57001 |
Tangent vector. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Tangent_vector&oldid=41536