Difference between revisions of "Predictable sigma-algebra"
From Encyclopedia of Mathematics
(Importing text file) |
m (wikilink) |
||
| Line 7: | Line 7: | ||
generated by all mappings <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074410/p0744106.png" /> of the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074410/p0744107.png" /> into <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074410/p0744108.png" /> that are (for each fixed <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074410/p0744109.png" />) continuous from the left (in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074410/p07441010.png" />) and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074410/p07441011.png" />-adapted to a non-decreasing family <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074410/p07441012.png" /> of sub-<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074410/p07441013.png" />-algebras <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074410/p07441014.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074410/p07441015.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074410/p07441016.png" /> is a measurable space. A predictable <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074410/p07441017.png" />-algebra can be generated by any of the following families of sets: | generated by all mappings <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074410/p0744106.png" /> of the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074410/p0744107.png" /> into <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074410/p0744108.png" /> that are (for each fixed <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074410/p0744109.png" />) continuous from the left (in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074410/p07441010.png" />) and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074410/p07441011.png" />-adapted to a non-decreasing family <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074410/p07441012.png" /> of sub-<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074410/p07441013.png" />-algebras <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074410/p07441014.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074410/p07441015.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074410/p07441016.png" /> is a measurable space. A predictable <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074410/p07441017.png" />-algebra can be generated by any of the following families of sets: | ||
| − | 1) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074410/p07441018.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074410/p07441019.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074410/p07441020.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074410/p07441021.png" /> is a stopping time (cf. [[Markov moment|Markov moment]]) and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074410/p07441022.png" /> a stochastic interval; | + | 1) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074410/p07441018.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074410/p07441019.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074410/p07441020.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074410/p07441021.png" /> is a stopping time (cf. [[Markov moment|Markov moment]]) and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074410/p07441022.png" /> a [[stochastic interval]]; |
2) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074410/p07441023.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074410/p07441024.png" />, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074410/p07441025.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074410/p07441026.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074410/p07441027.png" />. | 2) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074410/p07441023.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074410/p07441024.png" />, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074410/p07441025.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074410/p07441026.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074410/p07441027.png" />. | ||
Revision as of 06:34, 2 October 2016
predictable 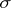 -algebra
-algebra
The least 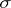 -algebra
-algebra 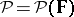 of sets in
of sets in
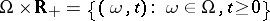 |
generated by all mappings 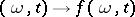 of the set
of the set 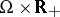 into
into 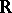 that are (for each fixed
that are (for each fixed 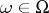 ) continuous from the left (in
) continuous from the left (in 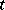 ) and
) and 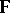 -adapted to a non-decreasing family
-adapted to a non-decreasing family 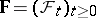 of sub-
of sub-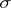 -algebras
-algebras 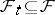 ,
, 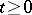 , where
, where 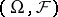 is a measurable space. A predictable
is a measurable space. A predictable 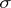 -algebra can be generated by any of the following families of sets:
-algebra can be generated by any of the following families of sets:
1) 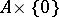 , where
, where 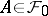 and
and 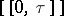 , where
, where  is a stopping time (cf. Markov moment) and
is a stopping time (cf. Markov moment) and 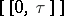 a stochastic interval;
a stochastic interval;
2) 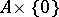 , where
, where 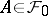 , and
, and 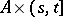 , where
, where 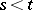 and
and  .
.
Between optional 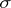 -algebras (cf. Optional sigma-algebra) and predictable
-algebras (cf. Optional sigma-algebra) and predictable 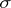 -algebras there is the relation
-algebras there is the relation  .
.
References
| [1] | C. Dellacherie, "Capacités et processus stochastique" , Springer (1972) |
Comments
Instead of "(s-) algebra" one more often uses (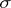 -) field.
-) field.
References
| [a1] | C. Dellacherie, P.A. Meyer, "Probabilities and potential" , A-C , North-Holland (1978–1988) (Translated from French) |
How to Cite This Entry:
Predictable sigma-algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Predictable_sigma-algebra&oldid=16866
Predictable sigma-algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Predictable_sigma-algebra&oldid=16866
This article was adapted from an original article by A.N. Shiryaev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article