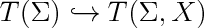|
|
| (87 intermediate revisions by the same user not shown) |
| Line 1: |
Line 1: |
| − | ====On terminology====
| + | <ref> [http://hea-www.harvard.edu/AstroStat http://hea-www.harvard.edu/AstroStat]; <nowiki> http://www.incagroup.org </nowiki>; <nowiki> http://astrostatistics.psu.edu </nowiki> </ref> |
| | | | |
| − | The term "standard probability space" is used in {{Cite|I}}. The same, or very similar, notion appears also as: "Lebesgue space" {{Cite|Ro}}, {{Cite|Ru}}, {{Cite|P}}, {{Cite|G}}; "standard Lebesgue space" {{Cite|G}}; "Lebesgue-Rohlin space" {{Cite|H}}, {{Cite|B}}; and "L. R. space" {{Cite|H}}.
| + | ====Notes==== |
| | + | <references /> |
| | | | |
| − | Some authors admit totally finite (not necessarily probability) measures {{Cite|P}}, {{Cite|B}}. Note also "standard σ-finite measure" in {{Cite|Mac}}. Some authors exclude spaces of cardinality higher than continuum ({{Cite|Ro}}, {{Cite|Ru}}, {{Cite|G}}, but not {{Cite|I}}, {{Cite|H}}, {{Cite|Mac}}, {{Cite|P}}, {{Cite|B}}) even though such space can be almost isomorphic to $(0,1)$ with Lebesgue measure (since it can contain a null set of arbitrary cardinality). Also, some authors do not insist on completeness {{Cite|B}}, {{Cite|G}}.
| + | ------------------------------------------- |
| | | | |
| − | ====Criticism====
| |
| | | | |
| − | According to {{Cite|Mal}},
| + | {| |
| − | * a measure is called separable if the corresponding $L_1$ space is separable {{Cite|Mal|Sect. IV.6.0}}; | + | | A || B || C |
| − | * every separable complete nonatomic probability space is isomorphic to $[0,1]$ with Lebesgue measure {{Cite|Mal|Sect. IV.6.4.2: "structure theorem (nonatomic case)"}}. | + | |- |
| − | The proof provides a measure preserving map from the given space to $[0,1]$ that generates the given σ-algebra. However, such map is not necessarily an isomorphism. Its image must be of full ''outer'' measure, but not of full ''inner'' measure, which is a manifestation of the "image measure catastrophe" (see {{Cite|KP|p. 94}}, {{Cite|D|p. 1002}}).
| + | | X || Y || Z |
| | + | |} |
| | + | |
| | + | |
| | + | |
| | + | ----------------------------------------- |
| | + | ----------------------------------------- |
| | + | |
| | + | $\newcommand*{\longhookrightarrow}{\lhook\joinrel\relbar\joinrel\rightarrow}$ |
| | + | |
| | + | <asy> |
| | + | size(100,100); |
| | + | label(scale(1.7)*'$T(\\Sigma)\hookrightarrow T(\\Sigma,X)$',(0,0)); |
| | + | </asy> |
| | + | |
| | + | <asy> |
| | + | size(220,220); |
| | + | |
| | + | import math; |
| | + | |
| | + | int kmax=40; |
| | | | |
| − | Further, in {{Cite|Mal|Sect. IV.6.4.3: "structure theorem (general case)"}} it is claimed that every separable (as defined there) complete probability space is standard (as defined here), which is wrong, of course.
| + | guide g; |
| | + | for (int k=-kmax; k<=kmax; ++k) { |
| | + | real phi = 0.2*k*pi; |
| | + | real rho = 1; |
| | + | if (k!=0) { |
| | + | rho = sin(phi)/phi; |
| | + | } |
| | + | pair z=rho*expi(phi); |
| | + | g=g..z; |
| | + | } |
| | + | |
| | + | draw (g); |
| | | | |
| − | ====References====
| + | defaultpen(0.75); |
| | + | draw ( (0,0)--(1.3,0), dotted, Arrow(SimpleHead,5) ); |
| | + | dot ( (1,0) ); |
| | + | label ( "$a$", (1,0), NE ); |
| | | | |
| − | {|
| + | </asy> |
| − | |valign="top"|{{Ref|I}}|| Kiyosi Itô, "Introduction to probability theory", Cambridge (1984). {{MR|0777504}} {{ZBL|0545.60001}}
| |
| − | |-
| |
| − | |valign="top"|{{Ref|Ru}}|| Thierry de la Rue, "Espaces de Lebesgue", ''Séminaire de Probabilités XXVII,'' Lecture Notes in Mathematics, '''1557''' (1993), Springer, Berlin, pp. 15–21. {{MR|1308547}} {{ZBL|0788.60001}}
| |
| − | |-
| |
| − | |valign="top"|{{Ref|H}}|| Jean Haezendonck, "Abstract Lebesgue-Rohlin spaces", ''Bull. Soc. Math. de Belgique'' '''25''' (1973), 243–258. {{MR|0335733}} {{ZBL|0308.60006}}
| |
| − | |-
| |
| − | |valign="top"|{{Ref|HN}}|| P.R. Halmos, J. von Neumann, "Operator methods in classical mechanics, II", ''Annals of Mathematics (2)'' '''43''' (1942), 332–350. {{MR|0006617}} {{ZBL|0063.01888}}
| |
| − | |-
| |
| − | |valign="top"|{{Ref|Ro}}|| V.A. Rokhlin, (1962), "On the fundamental ideas of measure theory", ''Translations (American Mathematical Society) Series 1,'' 10 (1962), 1–54. {{MR|0047744}} Translated from Russian: Рохлин, В. А. (1949), "Об основных понятиях теории меры", Математический Сборник (Новая Серия) 25(67): 107–150. {{MR|0030584}}
| |
| − | |-
| |
| − | |valign="top"|{{Ref|P}}|| Karl Petersen, "Ergodic theory", Cambridge (1983). {{MR|0833286}} {{ZBL|0507.28010}}
| |
| − | |-
| |
| − | |valign="top"|{{Ref|G}}|| Eli Glasner, "Ergodic theory via joinings", Amer. Math. Soc. (2003). {{MR|1958753}} {{ZBL|1038.37002}}
| |
| − | |-
| |
| − | |valign="top"|{{Ref|B}}|| V.I. Bogachev, "Measure theory", Springer-Verlag (2007). {{MR|2267655}} {{ZBL|1120.28001}}
| |
| − | |-
| |
| − | |valign="top"|{{Ref|Mac}}|| George W. Mackey, "Borel structure in groups and their duals", ''Trans. Amer. Math. Soc.'' '''85''' (1957), 134–165. {{MR|0089999}} {{ZBL|0082.11201}}
| |
| − | |-
| |
| − | |valign="top"|{{Ref|Mal}}||Paul Malliavin, "Integration and probability", Springer-Verlag (1995). {{MR|1335234}} {{ZBL|0874.28001}}
| |
| − | |}
| |