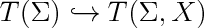|
|
| (157 intermediate revisions by the same user not shown) |
| Line 1: |
Line 1: |
| − | '''Measure algebra''' may refer to:
| + | <ref> [http://hea-www.harvard.edu/AstroStat http://hea-www.harvard.edu/AstroStat]; <nowiki> http://www.incagroup.org </nowiki>; <nowiki> http://astrostatistics.psu.edu </nowiki> </ref> |
| | | | |
| − | * algebra of measures on a topological group with the operation of convolution; see [[measure algebra (harmonic analysis)]];
| + | ====Notes==== |
| − | * normed Boolean algebra, either in general or consisting of equivalence classes of measurable sets; see [[measure algebra (measure theory)]].
| + | <references /> |
| | | | |
| − | =Measure algebra (measure theory)=
| + | ------------------------------------------- |
| | | | |
| − | {{MSC.|28Axx|28A50,60A10}}
| |
| | | | |
| − | [[:Category:Classical measure theory]]
| + | {| |
| | + | | A || B || C |
| | + | |- |
| | + | | X || Y || Z |
| | + | |} |
| | + | |
| | + | |
| | + | |
| | + | ----------------------------------------- |
| | + | ----------------------------------------- |
| | + | |
| | + | $\newcommand*{\longhookrightarrow}{\lhook\joinrel\relbar\joinrel\rightarrow}$ |
| | | | |
| − | {{TEX|done}}
| + | <asy> |
| | + | size(100,100); |
| | + | label(scale(1.7)*'$T(\\Sigma)\hookrightarrow T(\\Sigma,X)$',(0,0)); |
| | + | </asy> |
| | | | |
| − | $\newcommand{\Om}{\Omega}
| + | <asy> |
| − | \newcommand{\om}{\omega}
| + | size(220,220); |
| − | \newcommand{\F}{\mathcal F}
| |
| − | \newcommand{\A}{\mathcal A}
| |
| − | \newcommand{\M}{\mathcal M} $
| |
| − | A '''measure algebra''' is a pair $(B,\mu)$ where $B$ is a Boolean σ-algebra and $\mu$ is a (strictly) positive measure on $B$. The (strict) positivity means $\mu(x)\ge0$ and $\mu(x)=0\iff x=\bszero_B$ for all $x\in B$. However, about the greatest value $\mu(\bsone_B)$ of $\mu$, assumptions differ: from $\mu(\bsone_B)=1$ (that is, $\mu$ is a probability measure) in {{Cite|H2|p. 43}} and {{Cite|K|Sect. 17.F}} to $\mu(\bsone_B)<\infty$ (that is, $\mu$ is a totally finite measure) in {{Cite|G|Sect. 2.1}} to $\mu(\bsone_B)\le\infty$ in {{Cite|P|Sect. 1.4C}} and {{Cite|H1|Sect. 40}}.
| |
| | | | |
| − | A ''measure algebra of a measure space'' consists, by definition, of all equivalence classes of measurable sets. (Sets of the original σ-algebra or its completion give the same result.)
| + | import math; |
| | | | |
| − | This is "a coherent way to ignore the sets of measure $0$ in a measure space" {{Cite|P|page 15}}. "Many of the difficulties of measure theory and all the pathology of the subject arise from the existence of sets of measure zero. The algebraic treatment gets rid of this source of unpleasantness by refusing to consider sets at all; it considers sets modulo sets of measure zero instead." {{Cite|H2|page 42}}
| + | int kmax=40; |
| | | | |
| | + | guide g; |
| | + | for (int k=-kmax; k<=kmax; ++k) { |
| | + | real phi = 0.2*k*pi; |
| | + | real rho = 1; |
| | + | if (k!=0) { |
| | + | rho = sin(phi)/phi; |
| | + | } |
| | + | pair z=rho*expi(phi); |
| | + | g=g..z; |
| | + | } |
| | + | |
| | + | draw (g); |
| | | | |
| − | ====References====
| + | defaultpen(0.75); |
| | + | draw ( (0,0)--(1.3,0), dotted, Arrow(SimpleHead,5) ); |
| | + | dot ( (1,0) ); |
| | + | label ( "$a$", (1,0), NE ); |
| | | | |
| − | {|
| + | </asy> |
| − | |valign="top"|{{Ref|P}}|| Karl Petersen, "Ergodic theory", Cambridge (1983). {{MR|0833286}} {{ZBL|0507.28010}}
| |
| − | |-
| |
| − | |valign="top"|{{Ref|H1}}|| P.R. Halmos, "Measure theory", Van Nostrand (1950). {{MR|0033869}} {{ZBL|0040.16802}}
| |
| − | |-
| |
| − | |valign="top"|{{Ref|H2}}|| P.R. Halmos, "Lectures on ergodic theory", Math. Soc. Japan (1956). {{MR|0097489}} {{ZBL|0073.09302}}
| |
| − | |-
| |
| − | |valign="top"|{{Ref|G}}|| Eli Glasner, "Ergodic theory via joinings", Amer. Math. Soc. (2003). {{MR|1958753}} {{ZBL|1038.37002}}
| |
| − | |-
| |
| − | |valign="top"|{{Ref|K}}|| Alexander S. Kechris, "Classical descriptive set theory", Springer-Verlag (1995). {{MR|1321597}} {{ZBL|0819.04002}}
| |
| − | |-
| |
| − | |valign="top"|{{Ref|HN}}|| P.R. Halmos, J. von Neumann, "Operator methods in classical mechanics, II", ''Annals of Mathematics (2)'' '''43''' (1942), 332–350. {{MR|0006617}} {{ZBL|0063.01888}}
| |
| − | |-
| |
| − | |valign="top"|{{Ref|F}}|| D.H. Fremlin, "Measure theory", Torres Fremlin, Colchester. Vol. 1: 2004 {{MR|2462519}} {{ZBL|1162.28001}}; Vol. 2: 2003 {{MR|2462280}} {{ZBL|1165.28001}}; Vol. 3: 2004 {{MR|2459668}} {{ZBL|1165.28002}}; Vol. 4: 2006 {{MR|2462372}} {{ZBL|1166.28001}}
| |
| − | |}
| |