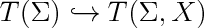|
|
| (180 intermediate revisions by the same user not shown) |
| Line 1: |
Line 1: |
| − | ''Also: Lebesgue-Rokhlin space''
| + | <ref> [http://hea-www.harvard.edu/AstroStat http://hea-www.harvard.edu/AstroStat]; <nowiki> http://www.incagroup.org </nowiki>; <nowiki> http://astrostatistics.psu.edu </nowiki> </ref> |
| | | | |
| − | {{MSC.|28Axx|28A50,60A10}}
| + | ====Notes==== |
| | + | <references /> |
| | | | |
| − | [[:Category:Classical measure theory]]
| + | ------------------------------------------- |
| | | | |
| − | {{TEX|done}}
| |
| | | | |
| − | $\newcommand{\Om}{\Omega}
| + | {| |
| − | \newcommand{\om}{\omega}
| + | | A || B || C |
| − | \newcommand{\F}{\mathcal F}
| + | |- |
| − | \newcommand{\B}{\mathcal B}
| + | | X || Y || Z |
| − | \newcommand{\M}{\mathcal M} $
| + | |} |
| − | A [[probability space]] is called '''standard''' if it satisfies the following equivalent conditions: | |
| − | * it is [[Measure space#Isomorphism|almost isomorphic]] to the real line with some [[probability distribution]] (in other words, a [[Measure space#Completion|completed]] [[Borel measure|Borel]] [[probability measure]], that is, a [[Lebesgue–Stieltjes integral|Lebesgue–Stieltjes]] probability measure);
| |
| − | * it is a [[standard Borel space]] endowed with a [[probability measure]], completed, and possibly augmented with a [[Measure space#null|null set]];
| |
| − | * it is [[Measure space#Completion|complete]], [[Measure space#Perfect and standard|perfect]], and the [[Hilbert space#L2 space|corresponding Hilbert space]] is separable.
| |
| | | | |
| − | ====The isomorphism theorem====
| |
| | | | |
| − | Every standard probability space consists of an [[Measure space#Atoms and continuity|atomic]] (discrete) part and an atomless (continuous) part (each part may be empty). The discrete part is finite or countable; here, all subsets are measurable, and the probability of each subset is the sum of probabilities of its elements.
| |
| | | | |
| − | '''Theorem 1.''' All atomless standard probability spaces are mutually almost isomorphic.
| + | ----------------------------------------- |
| | + | ----------------------------------------- |
| | | | |
| − | That is, up to almost isomorphism we have "the" atomless standard probability space. Its "incarnations" include the spaces $\R^n$ with atomless probability distributions (be they [[Continuous distribution|absolutely continuous]], [[Singular distribution|singular]] or mixed), as well as the set of all continuous functions $[0,\infty)\to\R$ with the [[Wiener measure]]. That is instructive: topological notions such as dimension do not apply to probability spaces.
| + | $\newcommand*{\longhookrightarrow}{\lhook\joinrel\relbar\joinrel\rightarrow}$ |
| | | | |
| − | ====Measure preserving maps====
| + | <asy> |
| | + | size(100,100); |
| | + | label(scale(1.7)*'$T(\\Sigma)\hookrightarrow T(\\Sigma,X)$',(0,0)); |
| | + | </asy> |
| | | | |
| − | The inverse to a bijective [[Measure space#measure preserving|measure preserving]] map is measure preserving provided that it is measurable; in this (not general) case the given map is a [[Measure space#Isomorphism|strict isomorphism]]. Here is an important fact in two equivalent forms.
| + | <asy> |
| | + | size(220,220); |
| | | | |
| − | '''Theorem 2a.''' Every bijective measure preserving map between standard probability spaces is a strict isomorphism.
| + | import math; |
| | | | |
| − | '''Theorem 2b.''' If $(\Om,\F,P)$ is a standard probability space and $\F_1\subset\F$ a sub-σ-field such that $(\Om,\F_1,P|_{\F_1})$ is also standard then $\F_1=\F$.
| + | int kmax=40; |
| | | | |
| − | Recall a topological fact similar to Theorem 2: if a bijective map between compact Hausdorff topological spaces is continuous then it is a homeomorphism. Moreover, if a Hausdorff topology is weaker than a compact topology then these two topologies are equal, which has the following measure-theory counterpart stronger than Theorem 2 (in two equivalent forms).
| + | guide g; |
| − | Here we call a probability space ''countably separated'' if its underlying measurable space is [[Measurable space#separated|countably separated]].
| + | for (int k=-kmax; k<=kmax; ++k) { |
| | + | real phi = 0.2*k*pi; |
| | + | real rho = 1; |
| | + | if (k!=0) { |
| | + | rho = sin(phi)/phi; |
| | + | } |
| | + | pair z=rho*expi(phi); |
| | + | g=g..z; |
| | + | } |
| | + | |
| | + | draw (g); |
| | | | |
| − | '''Theorem 3a.''' Every bijective measure preserving map from a standard probability space to a countably separated complete probability space is a strict isomorphism.
| + | defaultpen(0.75); |
| | + | draw ( (0,0)--(1.3,0), dotted, Arrow(SimpleHead,5) ); |
| | + | dot ( (1,0) ); |
| | + | label ( "$a$", (1,0), NE ); |
| | | | |
| − | '''Theorem 3b.''' If $(\Om,\F,P)$ is a standard probability space and $\F_1\subset\F$ is a countably separated sub-σ-field then $(\Om,\F,P)$ is the completion of $(\Om,\F_1,P|_{\F_1})$.
| + | </asy> |
| − | | |
| − | A continuous image of a compact topological space is always a compact set. In contrast, the image of a measurable set under a (non-bijective) measure-preserving map need not be measurable (indeed, the image of a null set need not be null; try the projection $\R^2\to\R^1$). Nevertheless, Theorem 4 (below) is a partial measure-theory counterpart, stronger than Theorem 3.
| |
| − | | |
| − | '''Theorem 4.''' Let $(\Om,\F,P)$ be a standard probability space, $(\Om_1,\F_1,P_1)$ a countably separated complete probability space, and $f:\Om\to\Om_1$ a measure preserving map. Then $(\Om_1,\F_1,P_1)$ is also standard, and $A_1\in\F_1\iff A\in\F$ whenever $A_1\subset\Om_1$ and $A=f^{-1}(A_1)$. In particular, the image $f(\Om)$belongs to $\F_1$. (See {{Cite|R|Th. 3-2}} and {{Cite|H|Prop. 9}}.)
| |
| − | | |
| − | ====Quotient spaces====
| |
| − | | |
| − | Theorem 4 (above) will be combined with the bijective correspondence between sub-σ-fields and linear sublattices described in the [[Measure space#Sub-σ-algebras and linear sublattices|corresponding section of "Measure space"]]. Here, as well as there, ''we restrict ourselves to σ-fields that contain all null sets.''
| |
| − | | |
| − | Every measure preserving map $\alpha:\Om\to\Om'$ between standard probability spaces $(\Om,\F,P)$ and $(\Om',\F',P')$ leads to an embedding $f\mapsto f\circ\alpha$ of Hilbert spaces, $L_2(\Om',\F',P')\to L_2(\Om,\F,P)$. It is, moreover, an embedding of linear lattices, and therefore $L_2(\Om',\F',P')=L_2(\Om,\F_1,P|_{\F_1})$ (both embedded into $L_2(\Om,\F,P)$) for some sub-σ-field $\F_1\subset\F$. Clearly, $\F_1$ is generated by $\alpha$ (up to the null sets), and we may say that $(\Om',\F',P')$ is the ''quotient space'' of $(\Om,\F,P)$ by $\F_1$ (via $\alpha$).
| |
| − | | |
| − | ''Existence.'' Let $(\Om,\F,P)$ be a standard probability space and $\F_1\subset\F$ a sub-σ-field; then $\F_1$ is generated by some $\alpha$ (as above), which means existence of a quotient space of $(\Om,\F,P)$ by $\F_1$. Here is how to do it. Using separability of $L_2(\Om,\F_1,P|_{\F_1})$ one constructs a measurable map $\alpha:\Om\to\Om'$ from $(\Om,\F,P)$ to a standard measurable space $(\Om',\B)$ such that a function of $L_2(\Om,\F,P)$ belongs to $L_2(\Om,\F_1,P|_{\F_1})$ if and only if it is of the form $g\circ\alpha$ for some measurable $g:\Om'\to\R$. Taking the image of the measure $P$ under $\alpha$ and applying Theorem 4 one gets a standard probability space $(\Om',\F',P')$ and a measure preserving map $\alpha:\Om\to\Om'$ that generates $\F_1$.
| |
| − | | |
| − | ''Uniqueness.'' If also $(\Om'',\F'',P'')$ is the quotient space of $(\Om,\F,P)$ by $\F_1$ (via $\beta$) then there exists an almost isomorphism $\gamma$ from $(\Om',\F',P')$ to $(\Om'',\F'',P'')$ such that $\gamma\circ\alpha=\beta$, which means uniqueness of the quotient space up to almost isomorphism.
| |
| − | | |
| − | Existence of $\gamma$ (above) follows from the following fact. Let $(\Om,\F,P)$, $(\Om',\F',P')$ and $(\Om'',\F'',P'')$ be standard probability spaces, and $\alpha:\Om\to\Om'$, $\beta:\Om\to\Om''$ measure preserving maps. If the sub-σ-field generated by $\beta$ is contained in the sub-σ-field generated by $\alpha$ then $\beta=\gamma\circ\alpha$ for some (almost unique) measure preserving map $\gamma:\Om'\to\Om''$. This is basically the Doob-Dynkin lemma.
| |
| − | | |
| − | Let $(\Om,\F,P)$ be a standard probability space, $\F_1,\F_2\subset\F$ two [[Independence#independent sigma-fields|independent]] sub-σ-fields, and $(\Om',\F',P')$, $(\Om'',\F'',P'')$ the corresponding quotient spaces (via $\alpha$, $\beta$); then the product space $(\Om',\F',P')\times(\Om'',\F'',P'')$ is the quotient space of $(\Om,\F,P)$ by $\sigma(\F_1,\F_2)$ (via $\alpha\times\beta:\omega\mapsto(\alpha(\omega),\beta(\omega))$). Here $\sigma(\F_1,\F_2)$ is the sub-σ-field generated by $\F_1,\F_2$. If, in addition, $\sigma(\F_1,\F_2)=\F$ then $\alpha\times\beta$ is an almost isomorphism from $(\Om,\F,P)$ to $(\Om',\F',P')\times(\Om'',\F'',P'')$. In this sense, any two independent sub-σ-fields $\F_1,\F_2$ that generate $\F$ decompose $(\Om,\F,P)$ into the product of two standard probability spaces (quotient spaces). The same holds for any finite or countable family of independent sub-σ-fields.
| |
| − | | |
| − | ====Conditional measures====
| |
| − | | |
| − | Let $\alpha:\Om\to\Om'$ be a measure preserving map between standard probability spaces $(\Om,\F,P)$ and $(\Om',\F',P')$.
| |
| − | | |
| − | '''Theorem 5a''' ''(existence).'' There exist families $(\F_{\om'})_{\om'\in\Om'}$, $(P_{\om'})_{\om'\in\Om'}$ of σ-fields $\F_{\om'}$ on $\Om$ and probability measures $P_{\om'}$ on $(\Om,\F_{\om'})$ such that for almost every $\om'\in\Om'$
| |
| − | * $(\Om,\F_{\om'},P_{\om'})$ is a standard probability space,
| |
| − | * $\alpha(\om)=\om'$ for $P_{\om'}$-almost all $\om\in\Om$,
| |
| − | and for every $A\in\F$
| |
| − | * the function $\om'\mapsto P_{\om'}(A)$ on $(\Om',\F',P')$ is measurable,
| |
| − | * $P(A)=\int_{\Om'} P_{\om'}(A)\,P'(\!\rd\om')$.
| |
| − | | |
| − | '''Theorem 5b''' ''(uniqueness).'' If also families $(\F'_{\om'})_{\om'\in\Om'}$, $(P'_{\om'})_{\om'\in\Om'}$ satisfy the requirements of Theorem 5a then $\F_{\om'}=\F'_{\om'}$ and $P_{\om'}=P'_{\om'}$ for almost all $\om'\in\Om'$.
| |
| − | | |
| − | The measure $P_{\om'}$ is called the conditional measure on the subset $\{\om:\alpha(\om)=\om'\}$ of $\Om$, or the conditional distribution of $\om$ given $\alpha(\om)=\om'$.
| |
| − | | |
| − | '''Example.''' The projection $(x,y)\mapsto x$ from the square $(0,1)\times(0,1)$ with the two-dimensional Lebesgue measure to the interval $(0,1)$ with the one-dimensional Lebesgue measure is a measure preserving map. The conditional distribution of $(x,y)$ given $x$ is the one-dimensional Lebesgue measure on the interval $\{x\}\times(0,1)$ with the one-dimensional Lebesgue measure. This example is trivial, but note the different σ-fields: neither $\F_{\om'}\subset\F$ nor $\F\subset\F_{\om'}$.
| |
| − | | |
| − | ====References====
| |
| − | | |
| − | {|
| |
| − | |valign="top"|{{Ref|I}}|| Kiyosi Itô, "Introduction to probability theory", Cambridge (1984). {{MR|0777504}} {{ZBL|0545.60001}}
| |
| − | |-
| |
| − | |valign="top"|{{Ref|Ru}}|| Thierry de la Rue, "Espaces de Lebesgue", ''Séminaire de Probabilités XXVII,'' Lecture Notes in Mathematics, 1557 (1993), Springer, Berlin, pp. 15–21. {{MR|1308547}} {{ZBL|0788.60001}}
| |
| − | |-
| |
| − | |valign="top"|{{Ref|H}}|| Jean Haezendonck, "Abstract Lebesgue-Rohlin spaces", ''Bull. Soc. Math. de Belgique'' '''25''' (1973), 243–258. {{MR|0335733}} {{ZBL|0308.60006}}
| |
| − | |-
| |
| − | |valign="top"|{{Ref|Ro}}|| V.A. Rokhlin, (1962), "On the fundamental ideas of measure theory", ''Translations (American Mathematical Society) Series 1,'' 10 (1962), 1–54. {{MR|0047744}} Translated from Russian: Рохлин, В. А. (1949), "Об основных понятиях теории меры", Математический Сборник (Новая Серия) 25(67): 107–150. {{MR|0030584}}
| |
| − | |}
| |