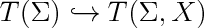|
|
| (273 intermediate revisions by the same user not shown) |
| Line 1: |
Line 1: |
| − | $\newcommand{\Om}{\Omega}
| + | <ref> [http://hea-www.harvard.edu/AstroStat http://hea-www.harvard.edu/AstroStat]; <nowiki> http://www.incagroup.org </nowiki>; <nowiki> http://astrostatistics.psu.edu </nowiki> </ref> |
| − | \newcommand{\A}{\mathcal A}
| |
| − | \newcommand{\B}{\mathcal B}
| |
| − | \newcommand{\M}{\mathcal M} $
| |
| − | The term '''"universally measurable"''' may be applied to
| |
| − | * a [[measurable space]];
| |
| − | * a subset of a measurable space;
| |
| − | * a [[metric space]].
| |
| | | | |
| − | '''Definition 1.''' Let $(X,\A)$ be a measurable space. A ''subset'' $A\subset X$ is called ''universally measurable'' if it is $\mu$-measurable for every finite measure $\mu$ on $(X,\A)$. In other words: $\mu_*(A)=\mu^*(A)$ where $\mu_*,\mu^*$ are the inner and outer measures for $\mu$, that is,
| + | ====Notes==== |
| − | : $ \mu_*(A) = \max\{\mu(B):B\in\A,B\subset A\}\,,\quad
| + | <references /> |
| − | \mu^*(A) = \min\{\mu(B):B\in\A,B\supset A\}\,.$
| |
| − | (See {{Cite|C|Sect. 8.4}}, {{Cite|S|p. 170}}.)
| |
| | | | |
| − | Universally measurable sets evidently are a σ-algebra that contains the σ-algebra $\A$ of measurable sets.
| + | ------------------------------------------- |
| | | | |
| − | ''Warning.'' Every measurable set is universally measurable, but an universally measurable set is generally not measurable! This terminological anomaly appears because the word "measurable" is used differently in two contexts, of measurable spaces and of measure spaces.
| |
| | | | |
| − | '''Definition 2.''' A separable ''metric space'' is called ''universally measurable'' if it is a universally measurable subset (as defined above) of its [[Metric space#completion|completion]]. Here the completion, endowed with the [[Measurable space#Borel sets|Borel σ-algebra]], is treated as a measurable space. (See {{Cite|S|p. 170}}, {{Cite|D|Sect. 11.5}}.)
| + | {| |
| | + | | A || B || C |
| | + | |- |
| | + | | X || Y || Z |
| | + | |} |
| | + | |
| | + | |
| | + | |
| | + | ----------------------------------------- |
| | + | ----------------------------------------- |
| | | | |
| − | '''Definition 3.''' A ''measurable space'' is called ''universally measurable'' if it is [[Measurable space#isomorphic|isomorphic]] to some universally measurable metric space (as defined above) with the Borel σ-algebra. (See {{Cite|S|p. 171}}.)
| + | $\newcommand*{\longhookrightarrow}{\lhook\joinrel\relbar\joinrel\rightarrow}$ |
| | | | |
| − | '''Theorem 1''' (Shortt {{Cite|S|Lemma 4}}). A [[Measurable space#countably generated|countably generated]] [[Measurable space#separated|separated]] measurable space $(X,\A)$ is universally measurable if and only if for every finite measure $\mu$ on $(X,\A)$ there exists a subset $A\in\A$ of full measure (that is, $\mu(X\setminus A)=0$) such that $A$ (treated as a [[Measurable space#subspace|subspace]]) is itself a [[standard Borel space]].
| + | <asy> |
| | + | size(100,100); |
| | + | label(scale(1.7)*'$T(\\Sigma)\hookrightarrow T(\\Sigma,X)$',(0,0)); |
| | + | </asy> |
| | | | |
| − | '''Theorem 2''' (Shortt {{Cite|S|Theorem 1}}). The following two conditions on a separable metric space are equivalent:
| + | <asy> |
| − | :(a) it is a universally measurable metric space;
| + | size(220,220); |
| − | :(b) the corresponding measurable space (with the Borel σ-algebra) is universally measurable.
| |
| | | | |
| − | Evidently, (a) implies (b); surprisingly, also (b) implies (a), which involves a Borel isomorphism (rather than isometry or homeomorphism) between two metric spaces.
| + | import math; |
| | | | |
| − | ====References==== | + | int kmax=40; |
| | | | |
| − | {|
| + | guide g; |
| − | |valign="top"|{{Ref|S}}|| Rae M. Shortt, "Universally measurable spaces: an invariance theorem and diverse characterizations", ''Fundamenta Mathematicae'' '''121''' (1984), 169–176. {{MR|0765332}} {{ZBL|0573.28018}}
| + | for (int k=-kmax; k<=kmax; ++k) { |
| − | |-
| + | real phi = 0.2*k*pi; |
| − | |valign="top"|{{Ref|N}}|| Togo Nishiura, "Absolute measurable spaces", Cambridge (2008). {{MR|2426721}} {{ZBL|1151.54001}}
| + | real rho = 1; |
| − | |-
| + | if (k!=0) { |
| − | |valign="top"|{{Ref|C}}|| Donald L. Cohn, "Measure theory", Birkhäuser (1993). {{MR|1454121}} {{ZBL|0860.28001}}
| + | rho = sin(phi)/phi; |
| − | |-
| + | } |
| − | |valign="top"|{{Ref|P}}|| David Pollard, "A user's guide to measure theoretic probability", Cambridge (2002). {{MR|1873379}} {{ZBL|0992.60001}}
| + | pair z=rho*expi(phi); |
| − | |-
| + | g=g..z; |
| − | |valign="top"|{{Ref|K}}|| Alexander S. Kechris, "Classical descriptive set theory", Springer-Verlag (1995). {{MR|1321597}} {{ZBL|0819.04002}}
| + | } |
| − | |-
| + | |
| − | |valign="top"|{{Ref|BK}}|| Howard Becker and Alexander S. Kechris, "The descriptive set theory of Polish group actions", Cambridge (1996). {{MR|1425877}} {{ZBL|0949.54052}}
| + | draw (g); |
| − | |-
| + | |
| − | |valign="top"|{{Ref|D}}|| Richard M. Dudley, "Real analysis and probability", Wadsworth&Brooks/Cole (1989). {{MR|0982264}} {{ZBL|0686.60001}}
| + | defaultpen(0.75); |
| − | |-
| + | draw ( (0,0)--(1.3,0), dotted, Arrow(SimpleHead,5) ); |
| − | |valign="top"|{{Ref|M}}|| George W. Mackey, "Borel structure in groups and their duals", ''Trans. Amer. Math. Soc.'' '''85''' (1957), 134–165. {{MR|0089999}} {{ZBL|0082.11201}}
| + | dot ( (1,0) ); |
| − | |-
| + | label ( "$a$", (1,0), NE ); |
| − | |valign="top"|{{Ref|H}}|| Paul R. Halmos, "Measure theory", v. Nostrand (1950). {{MR|0033869}} {{ZBL|0040.16802}}
| + | |
| − | |-
| + | </asy> |
| − | |valign="top"|{{Ref|R}}|| Walter Rudin, "Principles of mathematical analysis", McGraw-Hill (1953). {{MR|0055409}} {{ZBL|0052.05301}}
| |
| − | |}
| |