Namespaces
Variants
Actions

Difference between revisions of "User:Boris Tsirelson/sandbox1"

From Encyclopedia of Mathematics
Jump to: navigation, search
 
(309 intermediate revisions by the same user not shown)
Line 1: Line 1:
−
''Also: analytic measurable space''
+
<ref> [http://hea-www.harvard.edu/AstroStat http://hea-www.harvard.edu/AstroStat]; <nowiki> http://www.incagroup.org </nowiki>; <nowiki> http://astrostatistics.psu.edu </nowiki> </ref>
  
−
[[:Category:Classical measure theory]]
+
====Notes====
 +
<references />
  
−
{{User:Rehmann/sandbox/MSC|28A05|03E15,54H05}}
+
-------------------------------------------
  
−
$ \newcommand{\R}{\mathbb R}
 
−
\newcommand{\C}{\mathbb C}
 
−
\newcommand{\Om}{\Omega}
 
−
\newcommand{\A}{\mathcal A}
 
−
\newcommand{\B}{\mathcal B}
 
−
\newcommand{\P}{\mathbf P} $
 
−
A [[measurable space|Borel space]] $(X,\A)$ is called '''analytic''' if it is [[Measurable space#countably separated|countably separated]] and [[Measurable space#isomorphic|isomorphic]] to a [[Measurable space#quotient space|quotient space]] of a [[Standard Borel space|standard]] Borel space.
 
  
−
This is one out of several equivalent definitions (see below).
+
{|
 +
| A || B || C
 +
|-
 +
| X || Y || Z
 +
|}
 +
 
  
−
Finite and countable analytic Borel spaces are trivial: all subsets are measurable. Uncountable
 
−
analytic Borel spaces are of [[Continuum, cardinality of the|cardinality continuum]]. Some, but not all, of them are standard; these are mutually isomorphic. Some additional (to [[ZFC]]) set-theoretic axioms imply that all nonstandard analytic Borel spaces are mutually isomorphic (see [1, Sect. 26.D]).
 
  
−
''Non-example.'' The [[quotient group]] $\R/\Q$ (real numbers modulo rational numbers, additive) may be thought of as a quotient measurable space, $\R$ being endowed with its Borel σ-algebra. Then $\R/\Q$ is a quotient space of a standard Borel space, but not an analytic Borel space, because it is not countably separated. (See [2, Sect. 5].)
+
-----------------------------------------
 +
-----------------------------------------
  
−
====Relations to analytic sets====
+
$\newcommand*{\longhookrightarrow}{\lhook\joinrel\relbar\joinrel\rightarrow}$
  
−
A subset of a standard Borel space is called ''analytic'' if it is the image of a standard Borel space under a Borel map. (See [1, Sect. 14.A].)
+
<asy>
 +
size(100,100);
 +
label(scale(1.7)*'$T(\\Sigma)\hookrightarrow T(\\Sigma,X)$',(0,0));
 +
</asy>
  
−
As every subset of a measurable space, an analytic set is itself a measurable space (a subspace of the standard Borel space).
+
<asy>
 +
size(220,220);
  
−
'''Theorem 1a.''' If a bijective map between analytic sets is measurable then the inverse map is also measurable. (See [3, Sect. 4.5].)
+
import math;
  
−
====References====
+
int kmax=40;
−
{|
+
 
−
|valign="top"|[1]|| Alexander S.  Kechris, "Classical descriptive set theory", Springer-Verlag (1995). &nbsp; {{MR|1321597}} &nbsp;{{ZBL|0819.04002}}
+
guide g;
−
|-
+
for (int k=-kmax; k<=kmax; ++k) {
−
|valign="top"|[2]|| George W. Mackey, "Borel structure in groups and their duals", ''Trans.  Amer. Math. Soc.''  '''85''' (1957), 134–165. &nbsp; {{MR|0089999}} &nbsp;   {{ZBL|0082.11201}}
+
  real phi = 0.2*k*pi;
−
|-
+
  real rho = 1;
−
|valign="top"|[3]|| S.M. Srivastava, "A course on Borel sets", Springer-Verlag (1998). &nbsp; {{MR|1619545}} &nbsp;{{ZBL|0903.28001}}
+
  if (k!=0) {
−
|}
+
    rho = sin(phi)/phi;
 +
  }
 +
  pair z=rho*expi(phi);
 +
  g=g..z;
 +
}
 +
 
 +
draw (g);
 +
 
 +
defaultpen(0.75);
 +
draw ( (0,0)--(1.3,0), dotted, Arrow(SimpleHead,5) );
 +
dot ( (1,0) );
 +
label ( "$a$", (1,0), NE );
 +
 
 +
</asy>

Latest revision as of 07:12, 13 March 2016

[1]

Notes

  1. ↑ http://hea-www.harvard.edu/AstroStat; http://www.incagroup.org ; http://astrostatistics.psu.edu


A B C
X Y Z


$\newcommand*{\longhookrightarrow}{\lhook\joinrel\relbar\joinrel\rightarrow}$

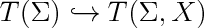
How to Cite This Entry:
Boris Tsirelson/sandbox1. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Boris_Tsirelson/sandbox1&oldid=20508
Retrieved from "https://encyclopediaofmath.org/index.php?title=User:Boris_Tsirelson/sandbox1&oldid=37839"