Natural number

One of the fundamental concepts in mathematics. Natural numbers may be interpreted as the cardinal numbers (cf. Cardinal number) of non-empty finite sets. The set of all natural numbers, together with the operations of addition and multiplication , forms the natural number system . In this system, both binary operations are associative and commutative and satisfy the distributivity law; 1 is the neutral element for multiplication, i.e. for any natural number ; there is no neutral element for addition, and, moreover, for any natural numbers 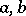. Finally, the following condition, known as the axiom of induction, is satisfied. Any subset of that contains 1 and, together with any element also contains the sum 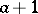, is necessarily the whole of 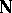. See Natural sequence; Arithmetic, formal.

References

[1]	, The history of mathematics from Antiquity to the beginning of the XIX-th century , 1 , Moscow (1970) (In Russian)
[2]	V.I. Nechaev, "Number systems" , Moscow (1975) (In Russian)
[3]	H. Davenport, "The higher arithmetic" , Hutchinson (1952)

Comments

A definition more elegant than the definition given above (the one of Frege–Russell) as cardinal numbers is von Neumann's definition, identifying a number with the set of its predecessors: 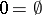, "n+ 1" 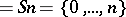. Here denotes "successor" . In this definition is taken to belong to (this is often done). In this case, is the neutral element for addition.

Cf. also Natural sequence.

References

[a1]	C.J. Scriba, "The concept of number, a chapter in the history of mathematics, with applications of interest to teachers" , B.I. Wissenschaftsverlag Mannheim (1968)