Difference between revisions of "Equality axioms"
From Encyclopedia of Mathematics
m (Provides an internal link for definition of reflexivity, term etc) |
|||
| Line 1: | Line 1: | ||
| − | Axioms regularizing the use of the equality relation in mathematical proofs. These axioms assert the [[reflexivity]] of the equality relation and the possibility of substituting equals for equals. Symbolically the equality axioms are written: | + | [[Axiom|Axioms]] regularizing the use of the equality relation in mathematical proofs. These axioms assert the [[reflexivity]] of the equality relation and the possibility of substituting equals for equals. Symbolically the equality axioms are written: |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035910/e0359101.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035910/e0359101.png" /></td> </tr></table> | ||
| Line 9: | Line 9: | ||
where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035910/e0359104.png" /> is a formula and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035910/e0359105.png" /> is a [[term]] in the language in question, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035910/e0359106.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035910/e0359107.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035910/e0359108.png" /> are variables having the same non-empty domain of variation, and expressions of the form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035910/e0359109.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035910/e03591010.png" /> denote the result of replacing all free occurrences of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035910/e03591011.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035910/e03591012.png" /> or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035910/e03591013.png" /> by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035910/e03591014.png" />. | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035910/e0359104.png" /> is a formula and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035910/e0359105.png" /> is a [[term]] in the language in question, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035910/e0359106.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035910/e0359107.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035910/e0359108.png" /> are variables having the same non-empty domain of variation, and expressions of the form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035910/e0359109.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035910/e03591010.png" /> denote the result of replacing all free occurrences of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035910/e03591011.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035910/e03591012.png" /> or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035910/e03591013.png" /> by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035910/e03591014.png" />. | ||
| − | Using equality | + | Using equality axioms, the symmetry and transitivity of the equality relation can be proved. To do this take <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035910/e03591015.png" /> to be the formula <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035910/e03591016.png" /> in the first case and the formula <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035910/e03591017.png" /> in the second. |
If the formulas and terms of the language in question are constructed from atomic formulas and terms using logical connectives and superposition, then the reduced equality axioms can be derived from their particular cases when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035910/e03591018.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035910/e03591019.png" /> are atomic formulas and terms. Symbolically: | If the formulas and terms of the language in question are constructed from atomic formulas and terms using logical connectives and superposition, then the reduced equality axioms can be derived from their particular cases when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035910/e03591018.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035910/e03591019.png" /> are atomic formulas and terms. Symbolically: | ||
Revision as of 15:22, 12 August 2015
Axioms regularizing the use of the equality relation in mathematical proofs. These axioms assert the reflexivity of the equality relation and the possibility of substituting equals for equals. Symbolically the equality axioms are written:
 |
 |
 |
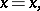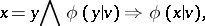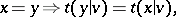where 
is a formula and 
is a term in the language in question, 
, 
and 
are variables having the same non-empty domain of variation, and expressions of the form 
and 
denote the result of replacing all free occurrences of 
in 
or 
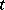by 
.
Using equality axioms, the symmetry and transitivity of the equality relation can be proved. To do this take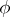 
to be the formula 
in the first case and the formula 
in the second.
If the formulas and terms of the language in question are constructed from atomic formulas and terms using logical connectives and superposition, then the reduced equality axioms can be derived from their particular cases when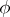 
and 
are atomic formulas and terms. Symbolically:
 |
 |
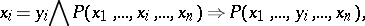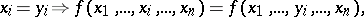where 
and 
are 
-place predicate and function symbols.
Comments
References
| [a1] | S.C. Kleene, "Introduction to metamathematics" , North-Holland (1950) pp. Chapt. XIV |
How to Cite This Entry:
Equality axioms. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Equality_axioms&oldid=36629
Equality axioms. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Equality_axioms&oldid=36629
This article was adapted from an original article by V.N. Grishin (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article