Namespaces
Variants
Actions

Difference between revisions of "User:Boris Tsirelson/sandbox2"

From Encyclopedia of Mathematics
Jump to: navigation, search
(Undo revision 35590 by Boris Tsirelson (talk))
 
(73 intermediate revisions by the same user not shown)
Line 1: Line 1:
−
the method is as follows:
+
==Experiments==
−
\begin{equation}
 
−
\begin{gathered}
 
−
k_1 = h f(x_0,y_0), \quad y_0 = y(x_0),\\
 
−
k_2 = h f \big( x_0 + \tfrac13 h, y_0 + \tfrac13 k_1 \big) \, , \\
 
−
k_3 = h f \big( x_0 + \tfrac13 h, y_0 + \tfrac16 k_1 + \tfrac16 k_2 \big) \, , \\
 
−
\end{gathered}
 
−
\end{equation}
 
  
 +
Note a fine distinction from [http://ada00.math.uni-bielefeld.de/MW1236/index.php/User:Boris_Tsirelson/sandbox#Experiments Ada]:
  
−
The number
+
<center><asy>
 +
fill( box((-1,-1),(1,1)), white );
 +
draw( (-1.2,-0.5)--(1.2,-0.5) );
 +
label("Just a text",(0,0));
 +
filldraw( box((-0.7,-1),(0.7,1)), white, opacity(0) );
 +
shipout(scale(15)*currentpicture);
 +
</asy></center>
  
 +
I guess, the reason is that there Asy generates pdf file (converted into png afterwards), and here something else (probably ps).
  
 +
No, it seems, it generates eps, both here and there. Then, what could be the reason?
  
 +
More.
  
 +
<center><asy>
 +
label("Just a text",(0,0));
 +
fill( box((-2,-1),(2,1)), white );
 +
//draw( box((-2,-1),(2,1)), green );
 +
shipout(scale(15)*currentpicture);
 +
</asy></center>
  
−
the method is as follows:
 
  
−
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/k/k056/k056060/k0560602.png" /></td> <td valign="top" style="width:5%;text-align:right;">(2)</td></tr></table>
+
<center><asy>
 +
label("Just a text",(0,0));
 +
fill( box((-2,-1),(2,1)), white );
 +
draw( box((-2,-1),(2,1)), green );
 +
shipout(scale(15)*currentpicture);
 +
</asy></center>
  
−
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/k/k056/k056060/k0560603.png" /></td> </tr></table>
+
Mysterious.
  
−
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/k/k056/k056060/k0560604.png" /></td> </tr></table>
+
==Three dimensions==
  
−
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/k/k056/k056060/k0560605.png" /></td> </tr></table>
+
<center><asy>
 +
settings.render = 0;
  
−
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/k/k056/k056060/k0560606.png" /></td> </tr></table>
+
unitsize(100);
  
−
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/k/k056/k056060/k0560607.png" /></td> </tr></table>
+
import three;
 +
import tube;
  
−
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/k/k056/k056060/k0560608.png" /></td> </tr></table>
+
import graph;
 +
path unitCircle = Circle((0,0),1,35);
  
−
The number
+
currentprojection = perspective((900,-350,-650));
 +
currentlight=light(gray(0.4),specularfactor=3,viewport=false,(-0.5,-0.5,-0.75),(0,-0.5,0.5),(0.5,0.5,0.75));
 +
// currentlight=light(gray(0.4),specularfactor=3,viewport=false,(-0.5,-0.5,-0.75),(0.5,-0.5,0.5),(0.5,0.5,0.75));
  
−
*******************************************
+
triple horn_start=(0,-1,0.6);
 +
triple horn_end=(0,0.4,0.2);
 +
real horn_radius=0.2;
  
−
[http://www.mediawiki.org/wiki/Extension_talk:MathJax#.5BWORKAROUND.5D_MathJax_works_in_preview.2C_but_not_in_page_display here]
+
real ratio=horn_end.z/(-horn_start.y);    // fractal levels ratio
  
−
$$\text{ $K$ compact}$$
+
transform3 implode_right = shift(horn_end) * scale3(ratio) * rotate(-90,X) * shift(-horn_start.y*Y);
 +
transform3 left_right = reflect(O,X,Z)*rotate(90,Y);
  
−
\[\text{ $K$ compact}\]
+
path[] cover_with_holes = scale(horn_radius/ratio)*unitCircle^^
 +
  shift((horn_start.z,0))*scale(0.9horn_radius)*reverse(unitCircle)^^
 +
  shift((-horn_start.z,0))*scale(0.9horn_radius)*reverse(unitCircle);
 +
surface cover = surface(cover_with_holes,ZXplane);
 +
surface cover_left = shift((horn_start.x,horn_start.y,0))*cover;
 +
surface two_covers = surface(cover_left,left_right*cover_left);
  
−
\begin{equation}
+
path3 horn_axis = horn_start..horn_start+(0,0.01,0)..(0,0,0.7)..(0,0.2,0.6)..horn_end+(0,0,0.01)..horn_end;
−
\mu (B)= \sup \{\mu(K): K\subset B, \text{ $K$ compact}\}\,  
 
−
\end{equation}
 
  
−
and having the following property:
+
surface horn = tube( horn_axis, scale(horn_radius)*unitCircle );
−
\begin{equation}\label{e:tight}
+
surface two_horns = surface(horn,reflect(O,X,Y)*horn);
−
\mu (B)= \sup \{\mu(K): K\subset B, \mbox{ $K$ compact}\}\,  
+
surface two_horns = surface(horn,reflect(O,X,Y)*horn);
−
\end{equation}
+
surface four_horns = surface(two_horns,left_right*two_horns,two_covers);
−
(see {{Cite|Sc}}).
 
  
 +
surface four_small_horns = implode_right*four_horns;
 +
surface eight_small_horns = surface(four_small_horns,left_right*four_small_horns);
  
−
The total variation measure of a $\mathbb C$-valued measure is defined on $\mathcal{B}$ as:
+
surface big_surface = surface(four_horns,eight_small_horns);
−
\[
 
−
\abs{\mu}(B) :=\sup\left\{ \sum \abs{\mu(B_i)}: \text{$\{B_i\}\subset\mathcal{B}$ is a countable partition of $B$}\right\}.
 
−
\]
 
−
In the real-valued case the above definition simplifies as
 
  
−
-----------------------
+
real R = horn_radius/ratio;
  
−
and the following identity  holds:
+
draw ( circle((0,1,0), 1.005R, Y ), currentpen+2 );
−
\begin{equation}\label{e:area_formula}
+
draw ( circle((horn_start.z,1.01,horn_start.x), horn_radius, Y ), currentpen+2 );
−
\int_A J f (y) \, dy =  \int_{\mathbb R^m} \mathcal{H}^0 (A\cap f^{-1} (\{z\}))\, d\mathcal{H}^n (z)\, .
+
draw ( circle((-horn_start.z,1.01,horn_start.x), horn_radius, Y ), currentpen+2 );
−
\end{equation}
 
  
−
Cp.  with 3.2.2 of {{Cite|EG}}. From \eqref{e:area_formula} it is not  difficult to conclude the following generalization (which also goes  often under the same name):
+
draw (big_surface, yellow);
  
 +
pen blackpen = currentpen+1.5;
  
 +
draw ( circle((0,-1,0), 1.005R, Y ), blackpen );
 +
draw ( circle(horn_start, 0.98horn_radius, Y ), blackpen );
 +
draw ( circle((horn_start.x,horn_start.y,-horn_start.z), 0.98horn_radius, Y ), blackpen );
  
 +
real phi=0.9;  // adjust to the projection
 +
triple u = (cos(phi),0,sin(phi));
 +
draw( R*u-Y -- R*u+Y, blackpen );
 +
draw( -R*u-Y -- -R*u+Y, blackpen );
  
−
\begin{equation}\label{ab}
+
</asy></center>
−
E=mc^2
+
 
−
\end{equation}
+
 
−
By \eqref{ab}, it is possible. But see \eqref{ba} below:
+
<center><asy>
−
\begin{equation}\label{ba}
+
settings.render = 0;
−
E\ne mc^3,
+
 
−
\end{equation}
+
size(200);
−
which is a pity.
+
import graph3;
 +
 
 +
currentprojection=perspective((2,2,5));
 +
 
 +
real R=1;
 +
real a=1;
 +
 
 +
real co=0.6;
 +
real colo=0.3;
 +
 
 +
triple f(pair t) {
 +
  return ((R+a*cos(t.y))*cos(t.x),(R+a*cos(t.y))*sin(t.x),a*sin(t.y));
 +
}
 +
 
 +
surface s=surface(f,(0,0),(2pi,2pi),20,20,Spline);
 +
 
 +
draw(s,rgb(co,co,co),meshpen=rgb(colo,colo,colo));
 +
 
 +
</asy></center>
 +
 
 +
==Sinusoid==
 +
 
 +
<center><asy>
 +
import graph;
 +
size(450);
 +
real f(real x) {return sin(x);};
 +
 
 +
real f1(real x) {return cos(x);};
 +
draw(graph(f1,-2*pi,2*pi),blue+1,"$\cos(x)$");
 +
draw(graph(f,-2*pi,2*pi),red+1,"$\sin(x)$");
 +
xaxis("$x$",Arrow);
 +
yaxis();
 +
 
 +
xtick("$\frac{\pi}{6}$",pi/6,N);
 +
xtick("$\frac{\pi}{4}$",pi/4,N);
 +
xtick("$\frac{\pi}{3}$",pi/3,N);
 +
xtick("$\frac{\pi}{2}$",pi/2,N);
 +
xtick("$\frac{3\pi}{2}$",3*pi/2,N);
 +
xtick("$\pi$",pi,N);
 +
xtick("$2\pi$",2*pi,N);
 +
xtick("$-\frac{\pi}{2}$",-pi/2,N);
 +
xtick("$-\frac{3\pi}{2}$",-3*pi/2,N);
 +
xtick("$-\pi$",-pi,N);
 +
xtick("$-2\pi$",-2*pi,N);
 +
 
 +
ytick("$1/2$",0.5,1,fontsize(8pt));
 +
ytick("$\sqrt{2}/2$",sqrt(2)/2,1,fontsize(8pt));
 +
ytick("$\sqrt{3}/2$",sqrt(3)/2,1,fontsize(8pt));
 +
ytick("$1$",1,1,fontsize(8pt));
 +
ytick("$-1/2$",-0.5,-1,fontsize(8pt));
 +
ytick("$-\sqrt{2}/2$",-sqrt(2)/2,-1,fontsize(8pt));
 +
ytick("$-\sqrt{3}/2$",-sqrt(3)/2,-1,fontsize(8pt));
 +
ytick("$-1$",-1,-1,fontsize(8pt));
 +
 
 +
attach(legend(),truepoint(E),10E,UnFill);
 +
</asy></center>
 +
 
 +
==Sinusoidal spiral==
 +
 
 +
<center><asy>
 +
import graph;
 +
size (200);
 +
 
 +
real r = 2.3;
 +
real m = 4;
 +
 
 +
real eps=10.^(-10);
 +
for  (int k=0; k<m; ++k) {
 +
  draw ( polargraph(  new real(real x) {return cos(m*x)^(1/m);}, -(pi/2m)+eps+k*2pi/m, (pi/2m)-eps+k*2pi/m ),
 +
defaultpen+1.5 );
 +
  draw ( -r*expi(-pi/2m+k*2pi/m)..r*expi(-pi/2m+k*2pi/m), dashed );
 +
  draw ( -r*expi(pi/2m+k*2pi/m)..r*expi(pi/2m+k*2pi/m), dashed );
 +
}
 +
label( "$m=4$", (0.58,0.02), fontsize(7pt) );
 +
 
 +
real eps=10.^(-2);
 +
for  (int k=0; k<m; ++k) {
 +
  draw ( polargraph(  new real(real x) {return cos(m*x)^(-1/m);}, -(pi/2m)+eps+k*2pi/m, (pi/2m)-eps+k*2pi/m ),
 +
defaultpen+1.5 );
 +
}
 +
label( "$m=-4$", (1.55,0.02), fontsize(7pt) );
 +
 
 +
label( "sinusoidal spiral: $a=1$", (0,2.3) );
 +
draw ( unitcircle, dashed );
 +
</asy></center>
 +
 
 +
==Power function==
 +
 
 +
<center><asy>
 +
import graph;
 +
picture whole;
 +
 
 +
real sc=0.8;
 +
 
 +
draw ( graph( new real(real x) {return x;}, -2, 2), red+1.2, "$y=x$" );
 +
draw ( graph( new real(real x) {return 2x;}, -1, 1), blue+1.2, "$y=2x$" );
 +
draw ( graph( new real(real x) {return x/2;}, -2, 2), green+1.2, "$y=x/2$" );
 +
 
 +
xaxis(-2.1,2.1, LeftTicks(Label(fontsize(8pt)),Step=1,step=0.2,Size=2,size=1,NoZero));
 +
yaxis(-2,2, RightTicks(Label(fontsize(8pt)),Step=0.5,step=0.1,Size=2,size=1,NoZero));
 +
labelx("$x$",(2.3,0.25));
 +
labely("$y$",(0.15,2.3));
 +
 
 +
add(scale(0.72sc,1.2sc)*legend(),(0.5,-0.75));
 +
 
 +
real mrg=1.3;
 +
draw( scale(mrg)*box((-2,-2),(2,2)), white );
 +
 
 +
add (whole,shift(-sc*230,0)*currentpicture.fit(sc*mrg*6.5cm));
 +
erase();
 +
 
 +
 
 +
draw ( graph( new real(real x) {return 1/x;}, -4, -0.25), red+1.2, "$y=1/x$" );
 +
draw ( graph( new real(real x) {return 1/x;}, 0.25, 4), red+1.2 );
 +
draw ( graph( new real(real x) {return 2/x;}, -4, -0.5), blue+1.2, "$y=2/x$" );
 +
draw ( graph( new real(real x) {return 2/x;}, 0.5, 4), blue+1.2 );
 +
draw ( graph( new real(real x) {return 1/(2x);}, -4, -0.125), green+1.2, "$y=1/(2x)$" );
 +
draw ( graph( new real(real x) {return 1/(2x);}, 0.125, 4), green+1.2 );
 +
 
 +
xaxis(-4.2,4.2, LeftTicks(Label(fontsize(8pt)),Step=2,step=0.5,Size=2,size=1,NoZero));
 +
yaxis(-4,4, RightTicks(Label(fontsize(8pt)),Step=1,step=0.2,Size=2,size=1,NoZero));
 +
labelx("$x$",(4.6,0.5));
 +
labely("$y$",(0.3,4.6));
 +
 
 +
add(scale(0.75sc,0.75sc)*legend(),(0.95,-1.2));
 +
 
 +
real mrg=1.3;
 +
draw( scale(mrg)*box((-4,-4),(4,4)), white );
 +
 
 +
add (whole,shift(0,0)*currentpicture.fit(sc*mrg*6.5cm,mrg*6.5cm,false));
 +
erase();
 +
 
 +
 
 +
draw ( graph( new real(real x) {return x^3;}, -4^(1/3), 4^(1/3)), red+1.2, "$y=x^3$" );
 +
draw ( graph( new real(real x) {return x^2;}, -2, 2), blue+1.2, "$y=x^2$" );
 +
draw ( graph( new real(real x) {return sqrt(x);}, 0, 4), green+1.2, "$y=x^{1/2}$" );
 +
draw ( graph( new real(real x) {return -sqrt(x);}, 0, 4), green+1.2 );
 +
 
 +
xaxis(-4.2,4.2, LeftTicks(Label(fontsize(8pt)),Step=2,step=0.5,Size=2,size=1,NoZero));
 +
yaxis(-4,4, RightTicks(Label(fontsize(8pt)),Step=1,step=0.2,Size=2,size=1,NoZero));
 +
labelx("$x$",(4.6,0.5));
 +
labely("$y$",(0.3,4.6));
 +
 
 +
add(scale(0.5sc,0.75sc)*legend(),(0.6,-2.5));
 +
 
 +
real mrg=1.3;
 +
draw( scale(mrg)*box((-4,-4),(4,4)), white );
 +
 
 +
add (whole,shift(sc*230,0)*currentpicture.fit(sc*mrg*6.5cm,mrg*6.5cm,false));
 +
erase();
 +
 
 +
shipout(whole);
 +
</asy></center>
 +
 
 +
==Kolmogorov test==
 +
 
 +
<center><asy>
 +
 
 +
srand(2014011);
 +
 
 +
import stats;
 +
 
 +
int size = 13;
 +
real [] sample = new real[size+1];
 +
real lambda = 1.3/size;
 +
real width = 2.0;
 +
 
 +
for (int k=0; k<size; ++k) {
 +
  sample[k] = Gaussrand();
 +
}
 +
sample[size] = 10;
 +
 
 +
sample = sort(sample);
 +
 
 +
// for (real x : sample ) {
 +
//  write(x);
 +
// }
 +
 
 +
real x0 = -10;
 +
int k = 0;
 +
for (real x : sample ) {
 +
  filldraw( box( (x0,k/size-lambda), (x,k/size+lambda) ), rgb(0.8,0.8,0.8) );
 +
  draw( (x0,k/size-lambda)..(x,k/size-lambda), currentpen+1.5 );
 +
  draw( (x0,k/size)..(x,k/size), currentpen+1.5 );
 +
  draw( (x0,k/size+lambda)..(x,k/size+lambda), currentpen+1.5 );
 +
  k += 1;
 +
  x0 = x;
 +
  draw( (x,(k-1)/size-lambda)..(x,k/size+lambda) );
 +
}
 +
 
 +
clip( box((-width,-0.005),(width,1.005)) );
 +
 
 +
draw ((-width,0)--(width,0),Arrow);
 +
draw ((0,-0.1)--(0,1.3),Arrow);
 +
draw ((-width,1)--(width,1));
 +
 
 +
draw ((sample[2],0)..(sample[2],2/size));
 +
draw ((sample[size-1],0)..(sample[size-1],0.48), dashed);
 +
draw ((sample[size-1],0.7)..(sample[size-1],1-1/size), dashed);
 +
 
 +
label("$x$",(width,0),S);
 +
label("$y$",(0,1.3),W);
 +
label("$0$",(0,0),SW);
 +
label("$1$",(0,1),NE);
 +
 
 +
label("$X_{(1)}$",(sample[0],0),S);
 +
label("$X_{(2)}$",(sample[1],0),S);
 +
label("$X_{(3)}$",(sample[2],0),S);
 +
label("$X_{(n)}$",(sample[size-1],0),S);
 +
 
 +
label("$F_n(x)+\lambda_n(\alpha)$",(-1.55,0.35));
 +
draw ((-1.35,0.25)..(-1.2,1/size+lambda));
 +
dot((-1.2,1/size+lambda));
 +
 
 +
label("$F_n(x)$",(0.4,0.3));
 +
draw ((0.4,0.4)..(0.3,8/size));
 +
dot((0.3,8/size));
 +
 
 +
label("$F_n(x)-\lambda_n(\alpha)$",(1.5,0.6));
 +
draw ((1.6,0.7)..(1.7,1-lambda));
 +
dot((1.7,1-lambda));
 +
 
 +
shipout(scale(100,100)*currentpicture);
 +
</asy></center>
 +
 
 +
==Golden ratio==
 +
 
 +
Strangely, the figure in EoM is erroneous! ED=EB, not BD=EB.
 +
 
 +
<center><asy>
 +
 
 +
pair A=(-1,0);
 +
pair B=(0,0);
 +
pair E=(0,0.5);
 +
pair C=A+(0.5*(sqrt(5)-1),0);
 +
pair D=(-1/sqrt(5), 0.5*(1-1/sqrt(5)));
 +
 
 +
draw( A--B--E--cycle,currentpen+1.5 );
 +
dot(A,currentpen+3.5); dot(B,currentpen+3.5); dot(E,currentpen+3.5); dot(C,currentpen+3.5); dot(D,currentpen+3.5);
 +
 
 +
draw( shift(E)*scale(0.5)*unitcircle,currentpen+1 );
 +
draw( shift(A)*scale(0.5*(sqrt(5)-1))*unitcircle,currentpen+1 );
 +
 
 +
draw( shift(B)*scale(0.5)*unitcircle, dashed+red );
 +
 
 +
clip(A+(-0.15,-0.15)--B+(0.15,-0.15)--E+(0.15,0.15)--A+(-0.15,0.15)--cycle);
 +
 
 +
label("$A$",A,S); label("$B$",B,S); label("$C$",C,S);
 +
label("$E$",E,N); label("$D$",D,N);
 +
 
 +
label( "\small Golden Ratio construction", (-0.5,0.8) );
 +
 
 +
shipout(scale(100)*currentpicture);
 +
</asy></center>
 +
 
 +
 
 +
 
 +
 
 +
 
 +
 
 +
 
 +
 
 +
[Calculus: ] the art of numbering and measuring exactly a thing whose existence cannot be conceived. (Voltaire, [http://www.fordham.edu/halsall/mod/1778voltaire-newton.asp Letter XVII: On Infinites In Geometry, And Sir Isaac Newton's Chronology])
 +
 
 +
And what are these fluxions? The velocities of evanescent increments? They are neither finite quantities, nor quantities infinitely small, nor yet nothing. May we not call them ghosts of departed quantities?  (Berkeley, [http://www-history.mcs.st-and.ac.uk/Quotations/Berkeley.html The Analyst])
 +
 
 +
 
 +
WARNING: Asirra, the cat and dog CAPTCHA, is closing permanently on October 6, 2014. Please contact this site's administrator and ask them to switch to a different CAPTCHA. Thank you!

Latest revision as of 20:14, 12 December 2014

Experiments

Note a fine distinction from Ada:

I guess, the reason is that there Asy generates pdf file (converted into png afterwards), and here something else (probably ps).

No, it seems, it generates eps, both here and there. Then, what could be the reason?

More.


Mysterious.

Three dimensions


Sinusoid

Sinusoidal spiral

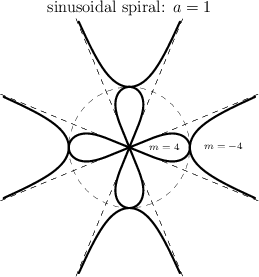
Power function

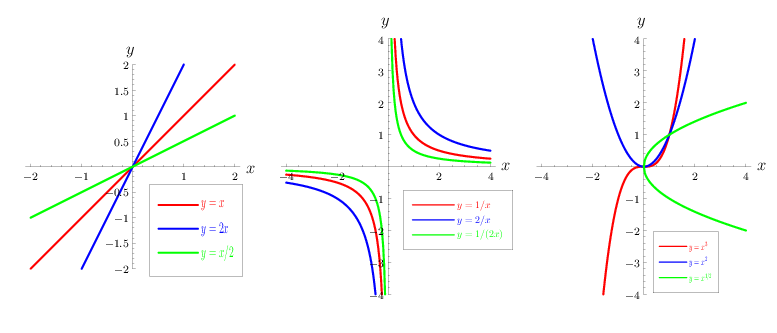
Kolmogorov test

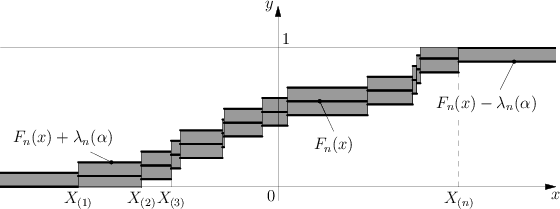
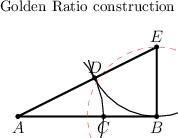
Golden ratio

Strangely, the figure in EoM is erroneous! ED=EB, not BD=EB.





[Calculus: ] the art of numbering and measuring exactly a thing whose existence cannot be conceived. (Voltaire, Letter XVII: On Infinites In Geometry, And Sir Isaac Newton's Chronology)

And what are these fluxions? The velocities of evanescent increments? They are neither finite quantities, nor quantities infinitely small, nor yet nothing. May we not call them ghosts of departed quantities? (Berkeley, The Analyst)


WARNING: Asirra, the cat and dog CAPTCHA, is closing permanently on October 6, 2014. Please contact this site's administrator and ask them to switch to a different CAPTCHA. Thank you!

How to Cite This Entry:
Boris Tsirelson/sandbox2. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Boris_Tsirelson/sandbox2&oldid=32516
Retrieved from "https://encyclopediaofmath.org/index.php?title=User:Boris_Tsirelson/sandbox2&oldid=35591"