Difference between revisions of "Predicate"
From Encyclopedia of Mathematics
m (linking instead of quoting the relation) |
m (quoting the link name) |
||
| Line 1: | Line 1: | ||
| − | A function whose values are statements about <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074350/p0743501.png" />-tuples of objects forming the values of its arguments. For <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074350/p0743502.png" /> a predicate is called a "property" , for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074350/p0743503.png" /> a [[relation]] ; propositions (cf. [[Proposition|Proposition]]) may be regarded as zero-place predicates. | + | A function whose values are statements about <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074350/p0743501.png" />-tuples of objects forming the values of its arguments. For <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074350/p0743502.png" /> a predicate is called a "property" , for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074350/p0743503.png" /> a [[relation|"relation"]] ; propositions (cf. [[Proposition|Proposition]]) may be regarded as zero-place predicates. |
In order to specify an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074350/p0743504.png" />-place predicate <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074350/p0743505.png" /> one must indicate sets <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074350/p0743506.png" /> — the domains of variation of the object variables <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074350/p0743507.png" />; most often one considers the case <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074350/p0743508.png" />. From the set-theoretical point of view a predicate is specified by a subset <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074350/p0743509.png" /> of the Cartesian product <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074350/p07435010.png" />. Here <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074350/p07435011.png" /> is taken to mean "the ordered tuple a1…an belongs to M" . The syntactic specification of an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074350/p07435012.png" />-place predicate is realized by exhibiting a formula of a logico-mathematical language containing <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074350/p07435013.png" /> free variables. The notion of a predicate dates back to Aristotle; the apparatus for operating with statements containing predicates is developed in mathematical logic (cf. [[Logical calculus|Logical calculus]]; [[Predicate calculus|Predicate calculus]]). | In order to specify an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074350/p0743504.png" />-place predicate <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074350/p0743505.png" /> one must indicate sets <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074350/p0743506.png" /> — the domains of variation of the object variables <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074350/p0743507.png" />; most often one considers the case <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074350/p0743508.png" />. From the set-theoretical point of view a predicate is specified by a subset <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074350/p0743509.png" /> of the Cartesian product <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074350/p07435010.png" />. Here <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074350/p07435011.png" /> is taken to mean "the ordered tuple a1…an belongs to M" . The syntactic specification of an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074350/p07435012.png" />-place predicate is realized by exhibiting a formula of a logico-mathematical language containing <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074350/p07435013.png" /> free variables. The notion of a predicate dates back to Aristotle; the apparatus for operating with statements containing predicates is developed in mathematical logic (cf. [[Logical calculus|Logical calculus]]; [[Predicate calculus|Predicate calculus]]). | ||
Revision as of 15:06, 20 May 2013
A function whose values are statements about 
-tuples of objects forming the values of its arguments. For 
a predicate is called a "property" , for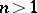 
a "relation" ; propositions (cf. Proposition) may be regarded as zero-place predicates.
In order to specify an 
-place predicate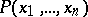 
one must indicate sets 
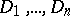— the domains of variation of the object variables 
; most often one considers the case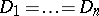 
. From the set-theoretical point of view a predicate is specified by a subset 
of the Cartesian product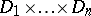 
. Here 
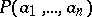is taken to mean "the ordered tuple a1…an belongs to M" . The syntactic specification of an 
-place predicate is realized by exhibiting a formula of a logico-mathematical language containing 
free variables. The notion of a predicate dates back to Aristotle; the apparatus for operating with statements containing predicates is developed in mathematical logic (cf. Logical calculus; Predicate calculus).
Comments
References
| [a1] | S.C. Kleene, "Introduction to metamathematics" , North-Holland (1952) pp. Chapt. XIV |
| [a2] | P. Suppes, "Introduction to logic" , v. Nostrand (1957) pp. §9.8 |
| [a3] | A. Grzegorczyk, "An outline of mathematical logic" , Reidel (1974) |
How to Cite This Entry:
Predicate. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Predicate&oldid=29766
Predicate. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Predicate&oldid=29766
This article was adapted from an original article by S.Yu. Maslov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article