Difference between revisions of "Isoperimetric inequality, classical"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 30: | Line 30: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> D.A. Kryzhanovskii, "Isoperimeters" , Moscow (1959) (In Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> H. Hadwiger, "Vorlesungen über Inhalt, Oberfläche und Isoperimetrie" , Springer (1957)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> L.A. Lyusternik, "Application of the Brunn–Minkowski inequality to extremal problems" ''Uspekhi Mat. Nauk'' , '''2''' (1936) pp. 47–54 (In Russian)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> H. Reichardt, "Einführung in die Differentialgeometrie" , Springer (1960)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> E. Schmidt, "Die Brunn–Minkowskische Ungleichung und ihr Spiegelbild sowie die isoperimetrische Eigenschaft der Kugel in der euklidischen und nichteuklidischen Geometrie I" ''Math. Nachr.'' , '''1''' (1948) pp. 81–157</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> H. Busemann, "The isoperimetric problem for Minkowski area" ''Amer. J. Math.'' , '''71''' (1949) pp. 743–762</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> E. De Giorgi, "Sulla proprietà isoperimetrica dell'ipersfera, nella classe degli insience aventi frontiera orientata di misura finita" ''Atti Acad. Naz. Lincei Mem. Cl. Sci. Fis., Mat. e Natur.'' , '''8''' : 5, 2 (1958) pp. 33–44</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> H. Federer, W.H. Fleming, "Normal and integer currents" ''Ann. of Math. (2)'' , '''72''' (1960) pp. 458–520</TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> T. Radó, "The isoperimetric inequality and the Lebesgue definition of surface area" ''Trans. Amer. Math. Soc.'' , '''61''' : 3 (1947) pp. 530–555</TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> L. Fejes Toth, "Lagerungen in der Ebene, auf der Kugel und im Raum" , Springer (1972)</TD></TR><TR><TD valign="top">[11]</TD> <TD valign="top"> V.I. Diskant, "A generalization of Bonnesen's inequalities" ''Soviet Math. Dokl.'' , '''14''' : 6 (1973) pp. 1728–1731 ''Dokl. Akad. Nauk SSSR'' , '''213''' : 3 (1973) pp. 519–521</TD></TR><TR><TD valign="top">[12]</TD> <TD valign="top"> V.I. Diskant, "Bounds for the discrepancy between convex bodies in terms of the isoperimetric difference" ''Siberian Math. J.'' , '''13''' : 4 (1973) pp. 529–532 ''Sibirsk. Mat. Zh.'' , '''13''' : 4 (1972) pp. 767–772</TD></TR><TR><TD valign="top">[13]</TD> <TD valign="top"> Yu.A. Volkov, "Stability of the solution to Minkowski's problem" ''Vestnik Leningrad. Univ. Ser. Mat. Astron.'' , '''18''' (1963) pp. 33–43 (In Russian)</TD></TR></table> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> D.A. Kryzhanovskii, "Isoperimeters" , Moscow (1959) (In Russian) {{MR|}} {{ZBL|}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> H. Hadwiger, "Vorlesungen über Inhalt, Oberfläche und Isoperimetrie" , Springer (1957) {{MR|0102775}} {{ZBL|0078.35703}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> L.A. Lyusternik, "Application of the Brunn–Minkowski inequality to extremal problems" ''Uspekhi Mat. Nauk'' , '''2''' (1936) pp. 47–54 (In Russian) {{MR|}} {{ZBL|}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> H. Reichardt, "Einführung in die Differentialgeometrie" , Springer (1960) {{MR|0116267}} {{ZBL|0091.34001}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> E. Schmidt, "Die Brunn–Minkowskische Ungleichung und ihr Spiegelbild sowie die isoperimetrische Eigenschaft der Kugel in der euklidischen und nichteuklidischen Geometrie I" ''Math. Nachr.'' , '''1''' (1948) pp. 81–157 {{MR|0028600}} {{ZBL|0030.07602}} </TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> H. Busemann, "The isoperimetric problem for Minkowski area" ''Amer. J. Math.'' , '''71''' (1949) pp. 743–762 {{MR|0031762}} {{ZBL|0038.10301}} </TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> E. De Giorgi, "Sulla proprietà isoperimetrica dell'ipersfera, nella classe degli insience aventi frontiera orientata di misura finita" ''Atti Acad. Naz. Lincei Mem. Cl. Sci. Fis., Mat. e Natur.'' , '''8''' : 5, 2 (1958) pp. 33–44 {{MR|}} {{ZBL|}} </TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> H. Federer, W.H. Fleming, "Normal and integer currents" ''Ann. of Math. (2)'' , '''72''' (1960) pp. 458–520 {{MR|}} {{ZBL|}} </TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> T. Radó, "The isoperimetric inequality and the Lebesgue definition of surface area" ''Trans. Amer. Math. Soc.'' , '''61''' : 3 (1947) pp. 530–555 {{MR|0021966}} {{ZBL|0035.32601}} </TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> L. Fejes Toth, "Lagerungen in der Ebene, auf der Kugel und im Raum" , Springer (1972) {{MR|}} {{ZBL|0229.52009}} </TD></TR><TR><TD valign="top">[11]</TD> <TD valign="top"> V.I. Diskant, "A generalization of Bonnesen's inequalities" ''Soviet Math. Dokl.'' , '''14''' : 6 (1973) pp. 1728–1731 ''Dokl. Akad. Nauk SSSR'' , '''213''' : 3 (1973) pp. 519–521 {{MR|338925}} {{ZBL|}} </TD></TR><TR><TD valign="top">[12]</TD> <TD valign="top"> V.I. Diskant, "Bounds for the discrepancy between convex bodies in terms of the isoperimetric difference" ''Siberian Math. J.'' , '''13''' : 4 (1973) pp. 529–532 ''Sibirsk. Mat. Zh.'' , '''13''' : 4 (1972) pp. 767–772 {{MR|}} {{ZBL|0266.52008}} </TD></TR><TR><TD valign="top">[13]</TD> <TD valign="top"> Yu.A. Volkov, "Stability of the solution to Minkowski's problem" ''Vestnik Leningrad. Univ. Ser. Mat. Astron.'' , '''18''' (1963) pp. 33–43 (In Russian) {{MR|}} {{ZBL|}} </TD></TR></table> |
| Line 42: | Line 42: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> T. Bonnesen, W. Fenchel, "Theorie der konvexen Körper" , Chelsea, reprint (1948) pp. Sects. 15, 29, 31, 38</TD></TR></table> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> T. Bonnesen, W. Fenchel, "Theorie der konvexen Körper" , Chelsea, reprint (1948) pp. Sects. 15, 29, 31, 38 {{MR|0344997}} {{MR|0372748}} {{MR|1512278}} {{ZBL|0277.52001}} {{ZBL|0906.52001}} {{ZBL|0008.07708}} {{ZBL|60.0673.01}} {{ZBL|51.0373.01}} </TD></TR></table> |
Revision as of 12:11, 27 September 2012
The inequality between the volume  of a domain in a Euclidean space
of a domain in a Euclidean space  ,
,  , and the
, and the  -dimensional area
-dimensional area  of the hypersurface bounding the domain:
of the hypersurface bounding the domain:
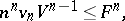 |
where  is the volume of the unit
is the volume of the unit  -sphere. Equality holds only for a sphere. The classical isoperimetric inequality gives a solution of the isoperimetric problem. For
-sphere. Equality holds only for a sphere. The classical isoperimetric inequality gives a solution of the isoperimetric problem. For  the classical isoperimetric inequality was known in Antiquity. A rigorous proof of the classical isoperimetric inequality for
the classical isoperimetric inequality was known in Antiquity. A rigorous proof of the classical isoperimetric inequality for 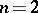 was given by F. Edler in 1882, for
was given by F. Edler in 1882, for 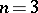 by H.A. Schwarz in 1890, and for all
by H.A. Schwarz in 1890, and for all 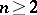 by L.A. Lyusternik in 1935 and E. Schmidt in 1939 (see [1], [2], [3]).
by L.A. Lyusternik in 1935 and E. Schmidt in 1939 (see [1], [2], [3]).
While in the two-dimensional case there are many proofs of the classical isoperimetric inequality (see [4]), only two approaches are known for  . The first is the method of symmetrization proposed by J. Steiner. Using this method, Schmidt obtained analogues of the classical isoperimetric inequality (and the Brunn–Minkowski inequalities) for spherical and hyperbolic
. The first is the method of symmetrization proposed by J. Steiner. Using this method, Schmidt obtained analogues of the classical isoperimetric inequality (and the Brunn–Minkowski inequalities) for spherical and hyperbolic  -dimensional spaces (see [5]). The second approach consists in reducing the classical isoperimetric inequality to a Brunn–Minkowski inequality (see Brunn–Minkowski theorem) and using the method of proportional division of volumes. In this approach there naturally arises the more general inequality
-dimensional spaces (see [5]). The second approach consists in reducing the classical isoperimetric inequality to a Brunn–Minkowski inequality (see Brunn–Minkowski theorem) and using the method of proportional division of volumes. In this approach there naturally arises the more general inequality
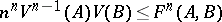 | (*) |
for volumes 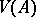 ,
, 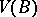 of two sets and the Minkowski area
of two sets and the Minkowski area 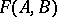 of the set
of the set 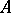 with respect to
with respect to 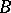 . The inequality (*) can be interpreted as a classical isoperimetric inequality in Minkowski space; equality for a fixed Minkowski "sphere"
. The inequality (*) can be interpreted as a classical isoperimetric inequality in Minkowski space; equality for a fixed Minkowski "sphere" 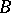 is not, generally speaking, attained for a unique body
is not, generally speaking, attained for a unique body 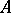 ; moreover, these bodies are different from a "sphere" (see [6]).
; moreover, these bodies are different from a "sphere" (see [6]).
There are a number of generalizations of the classical isoperimetric inequality in which one does not consider domains with a piecewise-smooth boundary, but wider classes of sets, and the area of the boundary is considered in a generalized sense (Minkowski area, Lebesgue area, Caccioppoli–De Giorgi perimeter of a set, or the mass of a current, see [7], [8]). The classical isoperimetric inequality remains valid in all these cases, as well as for hypersurfaces with self-intersections and the corresponding oriented volume (see [9]). These generalizations can be obtained from the classical isoperimetric inequality by limit transition for distinct variants of the concept of convergence.
For the isoperimetric difference 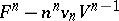 , and the isoperimetric ratio
, and the isoperimetric ratio 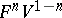 , estimates are known which strengthen the classical isoperimetric inequality (see [2]). Some of these estimates are obtained for sets of special shape, in the first place for convex sets (cf. Convex set) and polyhedra (see [10]). An example of this is the Bonnesen inequality for plane figures:
, estimates are known which strengthen the classical isoperimetric inequality (see [2]). Some of these estimates are obtained for sets of special shape, in the first place for convex sets (cf. Convex set) and polyhedra (see [10]). An example of this is the Bonnesen inequality for plane figures:
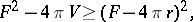 |
where  is the radius of the largest inscribed circle, and its generalization (see [11]) for convex bodies in
is the radius of the largest inscribed circle, and its generalization (see [11]) for convex bodies in 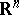 :
:
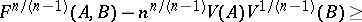 |
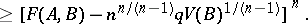 |
Here  . The relative isoperimetric difference of two convex bodies,
. The relative isoperimetric difference of two convex bodies,
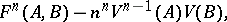 |
can serve as a measure of their non-homotheticity (see [12]). It is used, for example, in proving stability theorems in the Minkowski problem (see [13]). For generalizations of the classical isoperimetric inequality to spaces of variable curvature and related inequalities, see Isoperimetric inequality.
References
| [1] | D.A. Kryzhanovskii, "Isoperimeters" , Moscow (1959) (In Russian) |
| [2] | H. Hadwiger, "Vorlesungen über Inhalt, Oberfläche und Isoperimetrie" , Springer (1957) MR0102775 Zbl 0078.35703 |
| [3] | L.A. Lyusternik, "Application of the Brunn–Minkowski inequality to extremal problems" Uspekhi Mat. Nauk , 2 (1936) pp. 47–54 (In Russian) |
| [4] | H. Reichardt, "Einführung in die Differentialgeometrie" , Springer (1960) MR0116267 Zbl 0091.34001 |
| [5] | E. Schmidt, "Die Brunn–Minkowskische Ungleichung und ihr Spiegelbild sowie die isoperimetrische Eigenschaft der Kugel in der euklidischen und nichteuklidischen Geometrie I" Math. Nachr. , 1 (1948) pp. 81–157 MR0028600 Zbl 0030.07602 |
| [6] | H. Busemann, "The isoperimetric problem for Minkowski area" Amer. J. Math. , 71 (1949) pp. 743–762 MR0031762 Zbl 0038.10301 |
| [7] | E. De Giorgi, "Sulla proprietà isoperimetrica dell'ipersfera, nella classe degli insience aventi frontiera orientata di misura finita" Atti Acad. Naz. Lincei Mem. Cl. Sci. Fis., Mat. e Natur. , 8 : 5, 2 (1958) pp. 33–44 |
| [8] | H. Federer, W.H. Fleming, "Normal and integer currents" Ann. of Math. (2) , 72 (1960) pp. 458–520 |
| [9] | T. Radó, "The isoperimetric inequality and the Lebesgue definition of surface area" Trans. Amer. Math. Soc. , 61 : 3 (1947) pp. 530–555 MR0021966 Zbl 0035.32601 |
| [10] | L. Fejes Toth, "Lagerungen in der Ebene, auf der Kugel und im Raum" , Springer (1972) Zbl 0229.52009 |
| [11] | V.I. Diskant, "A generalization of Bonnesen's inequalities" Soviet Math. Dokl. , 14 : 6 (1973) pp. 1728–1731 Dokl. Akad. Nauk SSSR , 213 : 3 (1973) pp. 519–521 MR338925 |
| [12] | V.I. Diskant, "Bounds for the discrepancy between convex bodies in terms of the isoperimetric difference" Siberian Math. J. , 13 : 4 (1973) pp. 529–532 Sibirsk. Mat. Zh. , 13 : 4 (1972) pp. 767–772 Zbl 0266.52008 |
| [13] | Yu.A. Volkov, "Stability of the solution to Minkowski's problem" Vestnik Leningrad. Univ. Ser. Mat. Astron. , 18 (1963) pp. 33–43 (In Russian) |
Comments
The Minkowski area 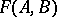 of a convex set
of a convex set 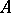 with respect to a convex set
with respect to a convex set 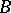 is defined as follows. Let
is defined as follows. Let 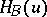 be the support function of
be the support function of 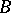 , i.e. for each vector
, i.e. for each vector  ,
, 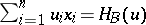 defines a supporting plane of
defines a supporting plane of 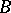 such that the open half-space into which
such that the open half-space into which  points contains no points of
points contains no points of 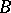 , so that
, so that 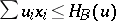 for all
for all  (and equality holds for at least one point of
(and equality holds for at least one point of 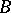 ). The Minkowski area of
). The Minkowski area of 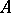 with respect to
with respect to 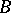 is now defined by
is now defined by
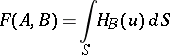 |
where 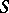 is the boundary of
is the boundary of 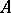 . It is also equal to
. It is also equal to  times the mixed volume
times the mixed volume 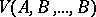 (
(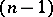
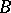 's). Here the mixed volume
's). Here the mixed volume 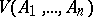 of
of  convex sets is defined as the coefficient of
convex sets is defined as the coefficient of 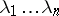 in the polynomial
in the polynomial 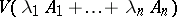 .
.
References
| [a1] | T. Bonnesen, W. Fenchel, "Theorie der konvexen Körper" , Chelsea, reprint (1948) pp. Sects. 15, 29, 31, 38 MR0344997 MR0372748 MR1512278 Zbl 0277.52001 Zbl 0906.52001 Zbl 0008.07708 Zbl 60.0673.01 Zbl 51.0373.01 |
Isoperimetric inequality, classical. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Isoperimetric_inequality,_classical&oldid=15338